�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�g�b�v�y�[�W
�Q�O�O�P�^�X�^�Q�P
�@�@�@�@�@�@�@�� ���[�U�[�W���C���ɂ��A��Όn�̑��݂͊m���ƂȂ�����
�@�q��@��P�b�g�ɓ��ڂ���Ă��郌�[�U�[�W���C���ɂ��A�����x�s�ς̌������j��Ă��邱�Ƃ��E�c����㓡
�@�@�@�@�@�@�@�� ���[�U�[�W���C���ɂ��A��Όn�̑��݂͊m���ƂȂ�����
�@�q��@��P�b�g�ɓ��ڂ���Ă��郌�[�U�[�W���C���ɂ��A�����x�s�ς̌������j��Ă��邱�Ƃ��E�c����㓡
�����ɂ�����Ă��܂��B
�@�Ƃ��낪�A���Θ_�w�҂́A���ΐ����_�������čI���ɔ��_���A���[�U�[�W���C���������Θ_���x��������̂��Ǝ�
�@�Ƃ��낪�A���Θ_�w�҂́A���ΐ����_�������čI���ɔ��_���A���[�U�[�W���C���������Θ_���x��������̂��Ǝ�
�����Ă���A�o������Ȃ���Ԃ̂܂܂��Ă���悤�Ɏv���܂��B
�@���̖����l���Ă��邤���ɁA���Θ_�h�����{�̂Ƃ���ő傫�Ȋ��Ⴂ�����Ă��邱�ƂɋC�Â��܂����B�����ł͑���
�@���̖����l���Ă��邤���ɁA���Θ_�h�����{�̂Ƃ���ő傫�Ȋ��Ⴂ�����Ă��邱�ƂɋC�Â��܂����B�����ł͑���
�_�h�̊��Ⴂ�𖾂炩�ɂ��܂��B
�m�����n
�@�܂��c�_�̖{���I�ȏœ_���A���_�_���Ƃ����`�ł܂��ꌾ�ŕ\�����Ă����܂��B
���_�_��
���[�U�[�W���C���̌��̋����́A��Όn��O��ɂ��Ȃ���ΐ��藧���Ȃ����̂ł���B
���́��_�_�������������ۂ����A�ő�̏œ_�ɂȂ��Ă��܂��B
�m�����n
�@�܂��c�_�̖{���I�ȏœ_���A���_�_���Ƃ����`�ł܂��ꌾ�ŕ\�����Ă����܂��B
���_�_��
���[�U�[�W���C���̌��̋����́A��Όn��O��ɂ��Ȃ���ΐ��藧���Ȃ����̂ł���B
���́��_�_�������������ۂ����A�ő�̏œ_�ɂȂ��Ă��܂��B
�����Θ_�h�́A��̘_�_�͐������ƌ����A����đ��ΐ����_�͊Ԉ���Ă���Ǝ咣���܂��i�������_�_�������������
���ʓI�ɂ��̂悤�ɂȂ�܂��j�B
�������A���Θ_�h�͏�̎咣�ɑ��Ă܂��^����ɑ��ΐ����_�������o���A���̂悤�ɔ��_���܂��B
�������A���Θ_�h�͏�̎咣�ɑ��Ă܂��^����ɑ��ΐ����_�������o���A���̂悤�ɔ��_���܂��B
���Θ_�h�̔��_
| ��]�̏�̌��̊ϑ��_�́A��]�n���Ȃ킿�����x�n�ɂ���̂�����A����͓��ꑊ�Θ_�̓K�p�͈͂ɂ͑����Ȃ��B��
���āA���̂��Ƃœ��ꑊ�Θ_�����ۂ��c�_������̂͂��������B����͉����x�n�ł��邩��A��ʑ��Θ_��p���Ȃ��� �Ȃ�Ȃ��B��ʑ��Θ_�Ōv�Z����E�E�E�Ƃ��Ă��낢��ƌv�Z���A�u�ق�A�܂������������Ȃ��B���Θ_�͐������̂��B�v �Ƃ��āA���߂�����B |
�@�����āA���̈�ʑ��Θ_�ł̌v�Z�������Ă��鍇���Ă��Ȃ��ŁA�܂����܂��܂ȋc�_������L�����Ă��܂��B
�@�������A�悭�l���Ă݂�E�E�E�E
���Θ_�h���咣�͂��������Ƃ������ƂɋC�Â��܂��B
�@�����ł̋c�_�̒��S�́A���[�U�[�W���C���̌��̋�������Όn��O��ɂ��Ȃ���ΐ��藧���Ȃ����̂Ȃ̂��ۂ��A��
�@�������A�悭�l���Ă݂�E�E�E�E
���Θ_�h���咣�͂��������Ƃ������ƂɋC�Â��܂��B
�@�����ł̋c�_�̒��S�́A���[�U�[�W���C���̌��̋�������Όn��O��ɂ��Ȃ���ΐ��藧���Ȃ����̂Ȃ̂��ۂ��A��
�������Ƃł��B��́��_�_���̐��ۂ��݂̂���ɂ��Ă���B
�@�����W���C���̌��̓������A��Όn���l���Ȃ���ΐ����̂��Ȃ����̂Ȃ�A���ꑊ�ΐ������͊ԈႢ�Ƃ������Ƃ�
�@�����W���C���̌��̓������A��Όn���l���Ȃ���ΐ����̂��Ȃ����̂Ȃ�A���ꑊ�ΐ������͊ԈႢ�Ƃ������Ƃ�
�Ȃ�A���Θ_�͕��܂��B����A������Όn�ƂȂ��W�̂Ȃ����̂Ȃ�A���̌��ۂ��瑊�Θ_���ے肳��邱�Ƃ�
����܂���B
���Ȃ݂ɁA��Όn�ƃG�[�e���͖��W�ł��i�������̈Ӗ����킩��Ȃ����́A<���Θ_�a���ߒ��ɂ�����l�@�̌���
������T�C�g>���Q�Ƃ��������j�B
�@���̋c�_�ł́A���̌��ۂ���K�R�I�ɐ�Όn���o�Ă��邩�ۂ����ő�̏œ_�Ȃ̂ł��B
�@�����܂ŗ���ƁA�C�Â����Ƃ�����ł��傤�B
����́A���̌��ۂ��������̂ɁA���Ȃ炸�������Θ_�������o���K�v�ȂǂȂ��A�Ƃ������Ƃł��B
���ꂪ���Θ_�h�̔��_�͂��������Ǝ����͂��߂ɏq�ׂ����R�ł��B
�@���Θ_�ȊO���ϓ_�����������A���̌��ʁA��Όn�̑��݁E�݂����炩�ɂȂ�A���̋c�_�͂܂���������ɏI
���ꂪ���Θ_�h�̔��_�͂��������Ǝ����͂��߂ɏq�ׂ����R�ł��B
�@���Θ_�ȊO���ϓ_�����������A���̌��ʁA��Όn�̑��݁E�݂����炩�ɂȂ�A���̋c�_�͂܂���������ɏI
���܂��B�����āA���̌��ʁA���̒i�K�Ƃ��đ��Θ_�̐��ۂ����f�����Ƃ������ꂾ���̂��Ƃł��B
���Θ_�������o����ΓI�ȕK�v���A�K�R���ȂǂȂ��̂ł��B
�@�ɂ�������炸�A��́��_�_�����ؖ�����̂ɁA���Θ_�h�́A�܂��^����ɑ��Θ_�������o���A����₱���Ɛ���
���Θ_�������o����ΓI�ȕK�v���A�K�R���ȂǂȂ��̂ł��B
�@�ɂ�������炸�A��́��_�_�����ؖ�����̂ɁA���Θ_�h�́A�܂��^����ɑ��Θ_�������o���A����₱���Ɛ���
����B���Θ_�łȂ���A���_�_���̐��ۂ������͖̂����Ƃł��v���Ă��邩�̂悤�ł��B�������A�����o���Ă���̂́A
�܂��\���ɂ͎�����Ă��Ȃ���ʑ��Θ_�ł���A�����͂ȂǂȂ����Ƃ͖��炩�ł����A�܂����������̊ϓ_������
���Θ_���Ԉ���Ă��邱�Ƃ́A��ʑ��ΐ����_���Ԉ���Ă��邱�Ƃ̏ؖ��Ŏ����ؖ������Ƃ���ł��B
�@��������A�܂�����������ϓ_�����������ؖ��ł���̂ł��B
�m�ؖ��n
�@���[�U�[�W���C���́A���̂̉�]�p���x�����o���鑕�u�ł��B
�@�q��@�̋@�̂ɉ����x�v�ƂƂ��ɂƂ����A�W���C������͋@�̂̌X���̏�A�܂������x�v����͈ʒu�̏�
�@��������A�܂�����������ϓ_�����������ؖ��ł���̂ł��B
�m�ؖ��n
�@���[�U�[�W���C���́A���̂̉�]�p���x�����o���鑕�u�ł��B
�@�q��@�̋@�̂ɉ����x�v�ƂƂ��ɂƂ����A�W���C������͋@�̂̌X���̏�A�܂������x�v����͈ʒu�̏�
�����A�������q��@�̐������p����i�s�����𒀎�����o���܂��B
���[�U�[�W���C���Ɖ����x�v�����킹�āA�����Z���T�Ƃ����܂��B
�@�@�̂��X����������Ƃ̎p���ɂ��ǂ��A�������͂��ꂻ���ɂȂ�@��𐳂��������ɂ��ǂ��B�����Z���T�́A�܂�
���[�U�[�W���C���Ɖ����x�v�����킹�āA�����Z���T�Ƃ����܂��B
�@�@�̂��X����������Ƃ̎p���ɂ��ǂ��A�������͂��ꂻ���ɂȂ�@��𐳂��������ɂ��ǂ��B�����Z���T�́A�܂�
���q��@�̓��]�̖�����S���Ă��܂��B
�@���[�U�[�W���C���ɂ́A�����O�E���[�U�[�W���C���ƌ��t�@�C�o�[�W���C���̂Q��ނ�����܂����{���I�Ȍ����͓�����
�@���[�U�[�W���C���ɂ́A�����O�E���[�U�[�W���C���ƌ��t�@�C�o�[�W���C���̂Q��ނ�����܂����{���I�Ȍ����͓�����
���B���[�U�[�W���C���́A���u�S�̂���]����ƌ��H���ɉ��������g�������������ꂩ�甭�����銱�Ȃ������o��
�œǂ݂Ƃ�A���̏���]�p���x�����o���܂��B
���[�U�[�W���C�����g���ƁA�@�̂̌X�������o�����̏���`���邱�ƂŁA�q��@�͂˂Ɉ��肵���悢�p����������
���[�U�[�W���C�����g���ƁA�@�̂̌X�������o�����̏���`���邱�ƂŁA�q��@�͂˂Ɉ��肵���悢�p����������
�Ƃ��ł��܂��i���ۂ͂R�������̂̉�]�p�����A���^�C���Ɍ��o���A�R�����I�ȏ��ɂ��p����������܂��j�B
�@���[�U�[�W���C���͂܂��������u���b�N�{�b�N�X�̒��ɒu����Ă��Ȃ����A�q��@�ɐ���Ȏp�����w�����A�����x�v��
�̈ʒu���Ƃ����킹�邱�ƂŁA�@�̂𐳂����ړI�n�܂ŗU�����Ă����B
���̎������̂��A��Όn�̑��݂��m���ɂ��Ă��邱�Ƃ͖����ł��B
�Ȃ��Ȃ�A������Όn�ȂǂƂ������̂��Ȃ����ɂƂ��āg�S�Ă̊����n����h�ȂǂƂ������ƂɂȂ�A�܂��q��@�̓�
�Ȃ��Ȃ�A������Όn�ȂǂƂ������̂��Ȃ����ɂƂ��āg�S�Ă̊����n����h�ȂǂƂ������ƂɂȂ�A�܂��q��@�̓�
�]�Ƃ��ėp����Ƃ������z���̂������т܂���B�v���悤�ɂ��ł��Ȃ�����ł��i����ƂȂ��ΓI�Ȋ���W��݂�
�邱�Ƃ��ł��Ȃ��I�j�B
�@�����������Όn�Ƃ�����������Ƃ�������i����W�j�����邩��A�@�̘̂A���I�ȌX�����̏��l����������
�@�����������Όn�Ƃ�����������Ƃ�������i����W�j�����邩��A�@�̘̂A���I�ȌX�����̏��l����������
���킹�邱�Ƃ��ۏ���A���m�Ȏp���E�ʒu�����肾����B�ŏ��̏o�����̏����p�����[���ɃZ�b�g���A�������珇��
�X�V���Ă������v�������ׂĂ��������B
��Όn�Ƃ����m�ł��鑫�ꂪ���邩�炱���A���n�_�ł̌v�Z�l���ۏ����B
��Όn�Ƃ����m�ł��鑫�ꂪ���邩�炱���A���n�_�ł̌v�Z�l���ۏ����B
�@������Όn�Ƃ������̂�z�肵�Ȃ���A��s�@�̓��]�ł��銵���Z���T�̐v����ł��܂���B���̂��Ƃ̓��[�U�[
�W���C���̐v���̂��A��ΓI��n�𑫏�Ɍ����i�s���邱�Ƃ�O��ɑg�ݗ��Ă��Ă���؋��Ȃ̂ł��B�܂��v
��̌v�Z�����ۂɂ݂Ă��A��Όn��z�肵���v�Z���Ȃ���Ă����B
�@����ɁA���̑��u�̐v�ɂ����ẮA�����n�A�����x�n�i��]�n�j�ȂǂƂ�����ʂ��Ȃ����K�v���Ȃ����Ƃ��킩��
�@����ɁA���̑��u�̐v�ɂ����ẮA�����n�A�����x�n�i��]�n�j�ȂǂƂ�����ʂ��Ȃ����K�v���Ȃ����Ƃ��킩��
�܂��B�u��]�n�͈�ʑ��Θ_�ŁA�����n�͓��ꑊ�Θ_�ŁE�E�v�ȂǂƂ���ȕ��ɐv�����Ă���̂ł͂Ȃ��A����Ȃ��Ƃ�
�͂����܂��Ȃ��ɁA�Z�p�҂͐�Όn�Ƃ������ΓI�Ȋ���W��p���āA�ÓT�����w�̔��e�Ń��[�U�[�W��
�C���Ƃ������u��v������Ă��܂��B�����āA�����ɂ��̑��u�͒������Ȑ��x�œ��삵�Ă���B
�@���ǁA����̋Z�p�҂����́A�}�N�X�E�F�����������A���Θ_�a���ȑO���펯�I�ϓ_����f���ɉ��߂����Ƃ�������
�ł��B
�^�̃}�N�X�E�F���������̓�̂������̎��@�������d�i���j���|���a�i���j�^�݂� �Ɓ@��^2��������a�i���j�����d�i���j�^�݂��@����
�^�̃}�N�X�E�F���������̓�̂������̎��@�������d�i���j���|���a�i���j�^�݂� �Ɓ@��^2��������a�i���j�����d�i���j�^�݂��@����
�g����������������܂����A����������Ƃ��̔g�̑��x�͂��ƂȂ�܂��B���ꂱ�����u�d���g�����Ƃ������x�ő�����
�n�Ƃ������ʂȑ��ꂪ����v�Ɖ�X�ɋ����Ă���Ă����ɂ�������炸�A�A�C���V���^�C���́u���ʂȌn�ȂǂȂ��B�S��
�̌n�͓������I�v�Ƃ�����������ꑊ�ΐ�������������ł����āA�d���C�w�̊�{���߂��ꒃ�ɂ��Ă��܂����B
�������A����Z�p�̑O�ɁA���ꑊ�ΐ������Ƃ��������̉R���������Ȃ��I�悵�Ă��܂��܂����B
�@���ǁA���Ƃ͐�Όn����ɑ������ő�����̂ł���A���̉^���n���猩���ꍇ���ȊO�̑����ɂȂ�Ƃ����A���Θ_
�a���ȑO�̕����w�҂Ȃ�N�����l�������߂ɋZ�p�҂͑f���ɏ]�����Ƃ������Ƃł���A���̉��߂ɑ����ă��[�U�[�W
���C����v���听�����݂��킯�ł��B
�@�u���b�N�{�b�N�X�̒��ɂ��Ȃ���A���[�U�[�W���C���́A�q��@������ɔ�Ԃ��߂̏��M���Â��Ă���A�Ƃ�
��������������x�悭�l���Ă݂Ă��������B
�@������Όn����ɐi�s���Ă��邱�Ƃ��A���̎������͂�����킩�邩��ł��B
�ؖ��I���B
�@��̐����������n�A�����x�n�܂������W�Ȃ��A�܂����ΐ����_�������o�����������g������Όn������
�@������Όn����ɐi�s���Ă��邱�Ƃ��A���̎������͂�����킩�邩��ł��B
�ؖ��I���B
�@��̐����������n�A�����x�n�܂������W�Ȃ��A�܂����ΐ����_�������o�����������g������Όn������
�����Ƃɒ��ڂ��Ăق����Ǝv���܂��B
�@�ȏォ��A�`���́��_�_���́A�������Ǝ��͔��f���܂��B
���ꑊ�ΐ������̔j�]�͖��炩�ŁA���Θ_���ے肳������Ƃ͂����܂ł��Ȃ��ł��傤�B
�@�ȏォ��A�`���́��_�_���́A�������Ǝ��͔��f���܂��B
���ꑊ�ΐ������̔j�]�͖��炩�ŁA���Θ_���ے肳������Ƃ͂����܂ł��Ȃ��ł��傤�B
�@����ɁA�㓡�����A�E�c����̃��[�U�[�W���C���Ɋւ���ڍׂȐ�������܂�邱�Ƃ������߂��܂��B���[�U�[�W���C��
�́A���݁A��s�@�݂̂Ȃ炸���P�b�g�A�~�T�C���A�l�H�q���A�w���R�v�^�A�����͂Ȃǂ���Ƃ�������̂ɓ��ڂ��ꂻ��
�p������ɋ��͂ȈЗ͂����Ă��܂��B
| ���㓡�����ɂ��A���܂��܂Ȗ{�ŁA�{�_���������������ړI�ȕ��@�������x�s�ϑ��j��̏ؖ����Ȃ���Ă��܂��B ��L�ؖ��́A�㓡�����̐����ɔ�ׂ�A����ԐړI�ȕ��@�Ƃ����邩������܂���B�������A��Όn�̑��݂����� �ɂ͂���ŏ\���Ȃ̂ł��B�㓡�����͉�]�n�A�����n�̋�ʂɂ���������������c�_������Ă��܂����A��̏ؖ����A ���̕K�v���Ȃ����Ƃ��킩��ł��傤�B |
�����[�U�[�W���C���Ɋւ���Q�l�_����
�@�E�u�p���Z���T�v���{�q��F���w��@��R�O���@��R�R�U���@�o�D�P�T�`�o�D�Q�T
�@�E�u�����O�E���[�U�[�W���C���̌���Ɖ��p�v���{�q��F���w��@��R�S���@��R�W�W���@�o�D�Q�V�`�o�D�R�S
�@�E�u���P�b�g�̃X�g���b�v�_�E���^�����U���V�X�e���v���{�q��F���w��@��R�P���@��R�T�V���@�o�D�S�O�`�o�D�S�V
�@�E�u�f�o�r�Ƃh�m�r�Ƃ̍q��@�̃n�C�u���b�h�q�@�v���{�q��F���w��@��R�T���@��R�X�U���@�o�D�Q�X�`�o�D�R�U
�@�E�u�F���p�W���C���̌����J���v���{�q��F���w��@��R�P���@��R�T�V���@�o�D�S�W�`�o�D�T�Q
�@�E�u���[�g�W���C���o�͐ϕ��ɂ��傤�o�H����v���{�q��F���w��@��Q�W���@��R�P�X���@�o�D�T�R�`�o�D�T�W
�@�E�u�����q�@���u�̊����f�q�v���{�q��F���w��@��R�P���@��R�T�R���@�o�D�R�Q�`�o�D�S�P
�@�E�u�p���Z���T�v���{�q��F���w��@��R�O���@��R�R�U���@�o�D�P�T�`�o�D�Q�T
�@�E�u�����O�E���[�U�[�W���C���̌���Ɖ��p�v���{�q��F���w��@��R�S���@��R�W�W���@�o�D�Q�V�`�o�D�R�S
�@�E�u���P�b�g�̃X�g���b�v�_�E���^�����U���V�X�e���v���{�q��F���w��@��R�P���@��R�T�V���@�o�D�S�O�`�o�D�S�V
�@�E�u�f�o�r�Ƃh�m�r�Ƃ̍q��@�̃n�C�u���b�h�q�@�v���{�q��F���w��@��R�T���@��R�X�U���@�o�D�Q�X�`�o�D�R�U
�@�E�u�F���p�W���C���̌����J���v���{�q��F���w��@��R�P���@��R�T�V���@�o�D�S�W�`�o�D�T�Q
�@�E�u���[�g�W���C���o�͐ϕ��ɂ��傤�o�H����v���{�q��F���w��@��Q�W���@��R�P�X���@�o�D�T�R�`�o�D�T�W
�@�E�u�����q�@���u�̊����f�q�v���{�q��F���w��@��R�P���@��R�T�R���@�o�D�R�Q�`�o�D�S�P

�Q�O�O1�^�P�O�^�T
�@�@�@�@�@�@�@�� ���Ǝ��Ԃ̍l�@�ŃA�C���V���^�C���͂R�d�̃~�X��Ƃ��Ă��遄
�@���ΐ����_�ł����������������킯�ł����A�����v�̍l�@�ɂ����ăA�C���V���^�C�����R�d�̃~�X��Ƃ��Ă��܂��B
�@�@�@�@�@�@�@�� ���Ǝ��Ԃ̍l�@�ŃA�C���V���^�C���͂R�d�̃~�X��Ƃ��Ă��遄
�@���ΐ����_�ł����������������킯�ł����A�����v�̍l�@�ɂ����ăA�C���V���^�C�����R�d�̃~�X��Ƃ��Ă��܂��B
����͂���܂ł̌��Ǝ��ԂɊւ���l�@���܂Ƃ߂�`�ŁA���̃~�X���q�ׂ����Ƃ������܂��B
�m�����n
�@����܂Ń}�C�P���\���E���[���[�����i�ȉ��l�l�����j������v�ł̌��̍l�@�Ɋւ��Č��㕨���w������Ă���_����
�m�����n
�@����܂Ń}�C�P���\���E���[���[�����i�ȉ��l�l�����j������v�ł̌��̍l�@�Ɋւ��Č��㕨���w������Ă���_����
�낢��w�E���܂������A���̒��S�I�Ȗ��_���Ȍ��ɐ�������ƁA���̂悤�ɂȂ�܂��B


�@��}���݂Ă��������B
�@����́A�u���ΐ����_�v�i���쓟�v���A��g���X�j���D�V�W�������v�̐}�Ƃقړ������̂ł��B
�����n�r���ɌŒ肳�ꂽ�C���������Ɍ������������鑕�u���l���A�r���͊����n�r�ɑ��Ă������ɑ��x�u�œ����Ă�
�@����́A�u���ΐ����_�v�i���쓟�v���A��g���X�j���D�V�W�������v�̐}�Ƃقړ������̂ł��B
�����n�r���ɌŒ肳�ꂽ�C���������Ɍ������������鑕�u���l���A�r���͊����n�r�ɑ��Ă������ɑ��x�u�œ����Ă�
��Ƃ��A���̌��ۂ��r����ϑ����Ă��܂��B
�n�r�����n�r�ɑ����ǂ�ȑ��x�ő����Ă��������n�ł������Ƃ��Ă��A�^��ɔ��˂��ꂽ���͂҂����苾�l�ɓ��B��
�n�r�����n�r�ɑ����ǂ�ȑ��x�ő����Ă��������n�ł������Ƃ��Ă��A�^��ɔ��˂��ꂽ���͂҂����苾�l�ɓ��B��
��B��������Ȃ��ƂɁA�u�x�N�g����������āA�E�}�ō��}���x�N�g���̒����������Ȃ��Ă���̂ɁA���̃x�N�g���̑�
�����́A�ˑR���l���ł���v�Ƃ��������ׂ����Ƃ������Ă���̂���}�ł��B
�@�܂����ɂ��Ȃ���Ȃ�Ȃ��_�́A�͂����Č��͐}�̂悤�Ȑi�s������̂��H�Ƃ������Ƃł��B
�@�܂����ɂ��Ȃ���Ȃ�Ȃ��_�́A�͂����Č��͐}�̂悤�Ȑi�s������̂��H�Ƃ������Ƃł��B
�w�҂́u���͏�}�̂悤�ɂ܂�Ŋ����̖@���ɏ]�����̂悤�ɐi�s����v�Ǝ咣���܂��B���́u��̂悤�Ȑi�s�͂��Ȃ��B
�}�N�X�E�F�������������͐�Όn�𑫏�ɐi�s���邩��A�^��ɕ����ꂽ���͐^��ɐi��ł��܂��̂ŋ��l�ɂ͓�
����Ȃ��B�v�Ǝ咣���܂��B
�@���́A��}�̂悤�Ȑi�s�͂��܂���B�����v�̌��̋����͌��Ȃ̂ł��B
�@���̗��R�́A���͏�}�̂悤�Ȋ����̖@���ɏ]�����悤�ȁi�܂�����̉^���ɉe����������悤�ȁj�i�s�͂����A��
�Όn����ɐi�ނ��Ƃ����Ɏ����Ŏ�����Ă��邩��ł��B���L�Ŏ����Ă��܂��B
�m���������̖@���ɏ]�킸�A��Όn����ɑ��邱�Ƃ���������n
�@���āA�Ȃ������w�҂��}�P�̌��̐i�s���x�����邩�Ƃ����ƁA���Θ_�̍��{�����ł�����ꑊ�ΐ����������邩��
�ł��B�������A���̌���������Ă��邱�Ƃ́A��L����Ŏ����ꂽ�ʂ�ł����A����ɂ��̌����������Ɋ�Ȃ��̂ł�
�邩�́A���u���ΐ������v�ɂ܂�����̏�Ȃ����j�̌o�܂𖾂炩�ɂ��遄�ŏڂ����q�ׂ܂����̂Ō��Ă�����
���B
�@���c�����͂��̒����u�Ȃ��Ƃ����鑊�ΐ����_�v�ŁA�����Ȃ��}�P�̂悤�ɐi�s���邩�̗��R��������Ă��܂����A
�@���c�����͂��̒����u�Ȃ��Ƃ����鑊�ΐ����_�v�ŁA�����Ȃ��}�P�̂悤�ɐi�s���邩�̗��R��������Ă��܂����A
���̐��������ł��邱�Ƃ́A�u�Ȃ��Ƃ����鑊�ΐ����_�v�̏d��~�X�̎w�E�Ŏ������Ƃ���ł��B�����ŁA���ӂ��Ăق�
���̂́A�}�P�̌��̐i�s�Ƃl�l�����̏c�����̌��̐i�s�Ƃ́A�{���I�ɓ����ł���Ƃ������Ƃł��B
���̂Ƃ���͋������悭��������Ă���A����䂦�Ɂu�Ȃ��Ƃ��E�E�v��p.45�Ń��[�U�[���u��p���Đ�������Ă���̂�
�����A���ꂪ�S���̒ʂ�Ȃ������ƂȂ��Ă���̂͂܂������c�O�ł��B
�@�P�O�O�N�O�Ȃ�A�����w�҂́A�}�N�X�E�F�����������݂Ȏ��Ɠ����l���łƂ炦�Ă��܂����B�u�d���g�͐�Όn����
���ɂ��ő���̂��v�ƁB
�������A���ΐ����_���a�������������ŁA�}�N�X�E�F�����������Ԉ������Ղ̏�łƂ炦��悤�ɂȂ��Ă��܂����B
����́A���ԁi����ɋ�ԁj���O��I�ɂ˂��Ȃ��邱�Ƃ����s����܂����B
�@�����܂łŁA���͂R�d�̃~�X�̂����Q�̃~�X��������Ă���̂ł������C�Â��ł��傤���B
�܂��A�}�P�ɂ����āA�^��ɕ����ꂽ���͂ق�Ƃ��͂��̂܂ܐ^��������ɐi�s����̂ɂ�������炸�A���ꑊ��
���������犵���̖@���ɏ]�����悤�ɐi�ށi���Ɍ����Ă����悤�ɐi�ށj�ƂƂ炦�Ă��܂������Ƃ��܂���P�Ԗڂ̃~�X�B
�@����ɂQ�ԖڂƂ��āA�����}�P�̂悤�Ɍ����i�s���i���̂Ɠ����̂悤�ɐi�݁j�r�n�̂悤�ȃx�N�g����`���̂Ȃ�A�c
�@����ɂQ�ԖڂƂ��āA�����}�P�̂悤�Ɍ����i�s���i���̂Ɠ����̂悤�ɐi�݁j�r�n�̂悤�ȃx�N�g����`���̂Ȃ�A�c
�����Ɖ������̑��x�x�N�g������������Ă���̂ł�����A�E�}�̂r�n�ł͑����͓��R�����傫���Ȃ�Ȃ���Ȃ�
�܂���B�Ƃ��낪�A�s�v�c�Ȃ��ƂɁA�r���n�̑傫�����̃x�N�g�����r�n�ł͒����x�N�g����`���Ă����Ȃ���A���x��
�����Łu�����x�s�ς̌����v�Ƃ������������������A���͂ǂ̌n�ɂ����Ă����Ȃ̂ŁA�E�}�i�r�n�j�ł̃x�N�g���̑傫����
�ł����Ƃ��Ă��܂������ƁA���ꂪ��Q�Ԗڂ̃~�X�ł����B
�@�}�P��肃�łȂ��͖̂��炩�ł����A����͒P���ȃ~�X�Ȃ̂ł��B
���w�A�����w�ɂ����āA�u���x�x�N�g���̒����͑����ɔ�Ⴓ���ĕ`���v�Ƃ����̂͊�{�I�ȋK���ł�����B
����͏����Ȑ��w�̃~�X�ł���A��ɋ������ׂ����̂ł͂���܂���B
�@�������A���낤���Ƃ��A�A�C���V���^�C���͎��Ԃ̒�`���˂��Ȃ��邱�ƂŁA�u����ŗ����͍����Ă���̂��I�v�Ǝ咣���A
�����Ă���ɂ݂���x����Ă��܂����B�����Ă���͂����Ȃ��̂ł��B
���Ԃ��ǂ̂悤�ɔP���Ȃ���ꂽ���A��̓I�Ȍv�Z�ɂ��ẮA
���������������B
�@���āA���͂R�Ԗڂ̃~�X�ł��B
���Ɂi�����܂ł����ɁI�j�A�P�Ԗڂ̃~�X�ƂQ�Ԗڂ̃~�X���~�X�łȂ��}�P�̌����v�̌��̐i�s�����������̂������Ƃ���
���A���������v�̎��Ԃ���X�̓���̕��ՓI�Ȏ��ԂƃC�R�[���Ƃ��Ă��܂����������A�v���I�ȃ~�X�ł����B
���Θ_�̎��Ԃ��A����̕��ՓI�Ȏ��Ԃ��܂��������т��Ȃ����̂ł��邱�Ƃ́A����܂ōĎO�q�ׂĂ����Ƃ����
���B
���Ȃ킿
�@�@�u�����v�̎��ԁv���u����̕��ՓI�Ȏ��ԁv
�@�@�u�����v�̎��ԁv���u����̕��ՓI�Ȏ��ԁv
�Ƃ��Ă��܂������Ƃ��A��R�Ԗڂ̃~�X�������킯�ł��B�����I���B
�ȏオ�A�`���ɂׂ̂��R�d�̃~�X�ł��B
���ΐ����_�́A���̂悤�ɂ��܂��܂ȃ~�X���܂�d�Ȃ��Ēa���������̂Ȃ̂ł��B
�ȏオ�A�`���ɂׂ̂��R�d�̃~�X�ł��B
���ΐ����_�́A���̂悤�ɂ��܂��܂ȃ~�X���܂�d�Ȃ��Ēa���������̂Ȃ̂ł��B

�@���q���e�⌴�q�͔��d�̃G�l���M�[�́A�L���Ȏ��d�������O2�́u���ʂƃG�l���M�[�̓������v�������ł���ƁA�]��
��茾���Ă��܂����B����͂܂�ő��Θ_�Ƃ������_�����������猴�q���e���ł������̂悤�ɂ��\������A���Θ_
�̐������̌���I�؋��̂悤�Ɍ��`����āA����ɂ������Ă���̂͏��m�̂Ƃ���ł��B
�@�Ƃ��낪�A�����͈���Ă���̂ł��B
�@�j����̋���ׂ����o�G�l���M�[�́A�ŏ��Ƀ}�C�g�i�[�ƃt���b�V�ɂ���ė��_�I�Ɍv�Z����܂������A����ɂ͑�
�@�j����̋���ׂ����o�G�l���M�[�́A�ŏ��Ƀ}�C�g�i�[�ƃt���b�V�ɂ���ė��_�I�Ɍv�Z����܂������A����ɂ͑�
�Θ_�Ȃǂ܂������p�����ɂȂ���܂����i�d�C�|�e���V�����E�G�l���M�[�ɂ��v�Z�ł����j�B��ɂȂ��āA�ނ�́A����
�_�̂d������^2��p���Ă������悤�Ȓl���ł�ƋC�Â����Ƃ������ƂȂ̂ł��B�d�C�|�e���V�����E�G�l���M�[�ł̌v�Z
�͌���ł��\���ʗp���܂��B
���̎����́A����u���q���e�v�i�R�c���ƒ��A�u���[�o�b�N�X�j��ǂ�ł͂��߂Ēm�������ƂȂ̂ł����A����́A���q
�͔��d�⌴�q���e�́A���ΐ����_������������a���������̂ł͂Ȃ��I�Ƃ��������ׂ��������A��L�{�����p��
�������܂��B
�m�����n
�m�����n
�{���D�Q�O�Q�`�Q�O�R
| �@�P�X�R�W�N�i���a�P�R�N�j�P�Q���X�g�b�N�z�����x�O�̐Â��ȓc�ɒ��Ń}�C�g�i�[�ƃt���b�V�����������悤�ɁA�E����
���q�j���O������̒����q���z�����錴�q�j�͂��̒����q�̎����Ă����G�l���M�[�����炢��̂Ō��q�j �̃G�l���M�[�͏オ��A���q�j�͐U�����J�n����B �@���̌��ʁA�^��������ɃX�^�C���̗ǂ������̃E�G�X�g�̂悤�ȁu���т�v�������A���̌��q�j�͂��т�����ɓ� �̕����ɕ�����A���q�j�͊j�̂���܂܂̃s�[�i�b�c�̂悤�Ȍ`�ɂȂ�A��́u�ӂ���݁v��������B���q�j �S�̂̓v���X�ɑѓd���Ă��邩��A���̓�̂ӂ���݂̊Ԃɂ��d�C�����͂ɂ��˗͂������A���݂��ɗ���� ���Ƃ���B �@�������j�͂ɋN������\�ʒ��͂����q�j�̕\�ʂɓ����Ă���A���ꂪ�j�̕\�ʐς��ŏ��ɂ��悤�Ɠ������ߊj �́i�\�ʒ��́j�̓s�[�i�b�c�^�ɂȂ������q�j��\�ʐύŏ��̋��`�Ɉ����߂����Ƃ���B�������j�͎͂��ߍ�p�� �����Ȃ��̂ŁA�j�͂ɋN������\�ʒ��͂́A��̂ӂ���݂����т��ʂ��Ă��������܂܂ł�����x�ȏ�ɗ� ��Ă��܂��ƁA�}���Ɏ�܂��Ă��܂��i���ߍ�p�݂̂Ȃ炸��������p��������d�C�����͂͂��قǎ�܂�Ȃ��j�B �@���̎������s�[�i�b�c�^�����`�Ɉ����߂����Ƃ���\�ʒ��͂���̂ӂ���݂������������Ƃ���d�C�����͂� �ł������Ƃ��ł��Ȃ�������A�j�͂��т�����ɂ��ĂЂ���A�j�͕���̕����ЂƂȂ邪�A���̕��� �ЊԂɑ��݂���d�C�����́i�˗́j�͏����邱�Ƃ͂Ȃ��̂œ�̕����Ђ͐����悭���݂������Ε����ɉ^�� �G�l���M�[���������������ł����B���炩�ɓd�C�����͂��j����̌����ł���B���̓d�C�����͂͌��q�j�� �ɒ�����ꂽ�d�C�|�e���V�����E�G�l���M�[�Ƃ��ĕ\�����Ƃ��ł���̂ŁA�j������o�����G�l���M�[�̌� �͂��łɊj���ɒ������Ă���d�C�|�e���V�����E�G�l���M�[�ł���B �@���������Ċj����@�\�͉����A�C���V���^�C���̗L���Ȃd�������O2�i���ʌ����j�Ȃǎg�킸�ɐ����ł���B���ꂪ �}�C�g�i�[�ƃt���b�V���^�����j��ŏ����j����̕����I���߂ł������B����Ƀ}�C�g�i�[�͂d�������O2���g���Ă� �j�������������B���̐����͑�Q�����E���u�����O�ɂȂ��ꂽ���̂ł���A�E�E�E�E�E |
�@���̂悤�Ɋj����ɂƂ��Ȃ��G�l���M�[�́A�d�C�|�e���V�����G�l���M�[�i�d�C�͂ƌ����Ă������ł����j��������
����A��L�̍Ō�̕��̂悤�ɂd�������O2�ł̉��߂Ƃ����̂́A��ɂȂ��ĂȂ��ꂽ���̂ł��邱�Ƃ��킩��ł��傤�B
�{��.�R�X�R�`�R�X�S
| �@�@���q���e���y������A������u�̋ʁv���`�������B���q���e�̑��G�l���M�[�̖�R�T�p�[�Z���g�͔M
�G�l���M�[�Ƃ��ĕ��o�����B�y������̉̋ʂ̒��a�͂P�O�O���[�g�����炢�ɂȂ�B�������O����̌��q���e�� ���x�́A���z�̓������x�i���S���x����P�O�O�O���x�j�ɂ܂ŏオ��A���q���e���̂��̑S������������ɃK�X�ɂȂ� �Ă��܂��B���������Ȃ�����ȂƂĂ��Ȃ����x�ɂ܂ŏオ��̂��H �@���q�j�P�̑傫���͂��悻�P�O�����̂P�Z���`���[�g���ł���B���̂悤�ȋɔ��Ȍ��q�j�������P����ɕ��� ���������łQ���d�q�{���g�̃G�l���M�[�����o�����̂ł���B�Q���d�q�{���g�̂����A���̂W�O�p�[�Z���g�ł���P ���U�O�O�O���d�q�{���g�͓�̕����Ђ��^�ԉ^���G�l���M�[�Ƃ��Č����B���q�j��������N�����Ɛ^����ɕ� ���Ёi���q�j�j�����������B�����ЂP�̉^�ԉ^���G�l���M�[�́A���̎��ʂɑ��x�̃j����|���ē�Ŋ������� �̂Ƃ��ĕ\�����i�����O2/2�F���͎��ʂ̒l��\�����͑��x��\���j�B �@���������ĕ����Ђ̑��x����{�ɂȂ�Ƃ��̉^���G�l���M�[�͎l�{�ƂȂ�A���x���O�{�ɂȂ�Ɖ^���G�l���M�[ �͋�{�A���x���l�{�ɂȂ�ƃG�l���M�[�͂P�U�{�ƂȂ�A�Ƃ�����ɑ��x�����������������ł��^���G�l���M�[�� ��������I��������̕����Ђ̃X�s�[�h�͕��ϕb���P�O�O�O�����[�g���i�����R�U�O�O���L�����[�g���I�j�Ō����x�� ��R�O���̂P�ł���B��������̕����ЂP�̉^���G�l���M�[�͂��̑��x�i�b���P�O�O�O�����[�g���j���j�悵���l�ɔ� �Ⴗ��i�P�O�O�O�����j�悷��Ƃ����ɂȂ邩�H�j�B���q�j�P�������ہA���̓�̕����Ђ̉^�ԉ^���G�l�� �M�[���P���U�O�O�O���d�q�{���g�Əo��͉̂E�̌v�Z�Ɋ�Â��Ă���B���̌v�Z�ɂ͂��łɑ��x���g���Čv�Z���Ă� ��̂ŁA�A�C���V���^�C���̎��d�������O2�͂��������g���Ă��Ȃ��B�E�E�E�E |
���F�F�͐��������܂����B
�@���̂悤�ɁA���̂������^���G�l���M�[�������Ђ́A���̌㑽���̕����ЂƂԂ��葬�x��ω���������
�ȓd���g�i�w���A�K���}�[���A�M���j����o���邱�ƂɂȂ�܂��B�i�d�ׂ������x�^������Γd���g����o���A���̍�
�^���G�l���M�[�͓d���g�̃G�l���M�[�ɓ]������Ă������Ƃɒ��Ӂj
�@���̂悤�ɍl����A�d�C�����͂���^���G�l���M�[�ւ����ēd���g���o�ւƂ������̓��ɂ����߂������Ƃ�
�@���̂悤�ɍl����A�d�C�����͂���^���G�l���M�[�ւ����ēd���g���o�ւƂ������̓��ɂ����߂������Ƃ�
���R���Ƃ������Ƃ��ł��܂��B�d�������O2�ł̉��߂́A�u���̂悤�ȉ��߂��\�ł���v�ƌ�ŒN�����C�t�����Ƃ����Ӗ�
���������Ă��܂���B���Θ_�Ƃ͂܂������W�̂Ȃ��Ƃ��납�猴�q���e�����܂ꂽ���Ƃ��킩��ł��傤�B
�@����́A�����Ռ��̎�����`���邽�߂ɏ����܂����B
�@�ȏ���A�̂��猾���Â��Ă����u���ΐ����_���a���������A�ŁA���q�̓G�l���M�[�̗��p���\�ƂȂ����I�v
�Ƃ������������S�Ɍ���ł���ƌ����܂��B����͑��ΐ����_�����Ă��i�܂��Ȃ��m���ɕ��܂����j�A���݂�
���q�͔��d�́A���ȏ��̋L�q�͑����C��������A�������Ȃ��Ɏ�����ƂȂ��A���̂܂c���Ă����Ƃ�������
�ł��B
�@�u���q���e�v�i�u���[�o�b�N�X�j�́A�j�����������猴�������܂ł��A�Տꊴ���ӂ��^�b�`�ł����������̂ŁA�ǂ��
����Ǝ��������j�̕���ɗ����Ă��邩�̍��o�����ڂ������Ă���閼���ł��B
��ǂ��������߂��܂��B
�@���Θ_�ɂ����鑊�Α��x�Ɋւ��ẮA�������x�s�ς̌����ɂ�����V�p���h�b�N�X�̒��Ńp���h�b�N�X���
���̖������w�E���܂������A�������x�̖ʂ�����V�����p���h�b�N�X�����o���܂����B��̂��̂Ɩ{���͓����ł����B
���ΐ����_�������܂Ő������Ǝ咣�������́A���̓��ɒ��킳��Ă͂������ł��傤���B
�m�ڍׁn
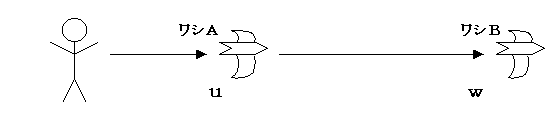
�@�}�̂悤�ɑ�n�i�j�n�Ƃ���j�ɗ������l�ɑ��đ��x���Ŕ��ł��郏�V�`�ƁA����ɂ��̃��V�`�ɑ��Ă��̑��x��
���ł��郏�V�a������Ƃ��܂��B
���܁A������j�n�̒��ł̕��̂̉^���ƍl���A�l�ɑ��鑊�Α��x�����߂Ă݂܂��B�j�n�Ƃ�����̌n���ōl����
���܂�����A�l����݂����V�a�̑��x���͂�+���ƂȂ邱�Ƃ͎����ł��B���Ȃ킿�A�l�́A���V�a��������+���Ŕ��ł����
�ϑ������킯�ł��B���̏ꍇ���@�Ƃ��܂��傤�B
�@���āA���Ƀ��V�`���j�L�n�̑�\�i�j�L�n�̌��_�ɌŒ肳��Ă���Ƃ���j�Ƃ��A����Ƀ��V�a���j�L�L�n�̑�\�ƌ��܂��B
����ƁA���x�͂j�n�A�j�L�n�A�j�L�L�n�Ƃ����R�n�Ԃ̉^����_����`�ƂȂ�A���ΐ����_�ł̌n�Ԃ̍������x�̌v�Z��
��A�l����݂����V�a�̑��x���́A
�@�@�@�����i��+���j�^�i1�{����/��^2�j
�@
�ƂȂ�܂��B���̏ꍇ���A�Ƃ��܂��傤�B���̏ꍇ�A�l�́A���V�a�������i��+���j�^�i1�{����/��^2�j�Ŕ��ł���Ɗϑ�
�����킯�ł��B
�@��Ȃ��ƂɂȂ�܂����B
�Ȃ�ƁA�@�ƇA�ŁA�l���猩�郏�V�a�̑��Α��x�����قȂ��Ă���̂ł��B
�^���͈�ł�����A����͑S�����������킯�ŁA�܂��Ƀp���h�b�N�X���������Ă����̂ł��B�@�ƇA�́A�����I
�ɂ͑S�������ȏł��邱�Ƃ͂����܂ł�����܂���B
�i���킸�����Ȃ̒��ӂł����A�@�����R���Θ_���g���Ă̋c�_�ł��̂ŁA���̓_�͌�����Ȃ��ł��������ˁB�j
�@���̂悤�ɂȂ�疳���Ȑݒ�������Ƃ��A���ΐ����_��K�p����ƁA���R�Ɍ���I�ȃp���h�b�N�X���������Ă��܂�����
�ɂȂ�܂��B���̃p���h�b�N�X�͑S���v���I�ŁA�����]�n�͂Ȃ��悤�Ɏ��̖ڂɂ͂���̂ł����A�F�l�͂ǂ̂悤��
�l������ł��傤���B���̃p���h�b�N�X���u�������x�̐V�p���h�b�N�X�v�Ɩ��t���A�u�����x�s�ς̌����ɂ�����V�p
���h�b�N�X�v�ƂƂ��ɍ���l�X�ɋc�_����邱�Ƃ�]�݂܂��B
�i���߁j
�Ȃ��n�Ԃł̍������x����L�̂悤�Ȍ��ʂɂȂ�̂��A�O�̂��ߏ��������Ȍv�Z�Ŏ����Ă����܂��B
�m�������Α��x�̌v�Z�n
�A�̏ꍇ�A�@���ꑊ�Θ_�ɂ��A�j�n�Ƃj�L�n�̕ϊ��͎��̃��[�����c�ϊ��Ō���Ă��܂��B
�@�������i���|�����j�^��i�P�|(��/c)^2�j�A�@���������A�@�@���������A�@�@�������i���|�����^��^2�j�^��i�P�|(��/c)^2�j�@�E�E�E�E�@
���l��K�L�n��K�L���n�̊Ԃ̕ϊ��́A���̂悤�ɂȂ�܂��B
���L�L���i�����|�������j�^��i�P�|(��/c)^2�j�A�@���L�L�������A�@���L�L�������A���L�L���i�����|�������^��^2�j�^��i�P�|(��/c)^2�j�E�E�A
�A�̉E�ӂɇ@�������Đ�������ƁA
���L�L���m���|�i(���{��)�^(�P�{�����^���O2)�j���n�^��i�P�|�i�P�^��^2�j�i(���{��)�^(�P�{�����^��^2�j�j)�E�E�E�B
�ƂȂ�܂��i���L�L�͗����܂����A�ȉ��̌��ʂ͓����ɂȂ�܂��j�B
���āA�j�L�L�n�̂j�n�ɑ��鑬�������Ƃ���ƁA�j�L�L�n�Ƃj�n�̊Ԃ̃��[�����c�ϊ��͎��ƂȂ�܂��B
�@���L�L���i���|�����j�^��i�P�|(���^��)�O2�j�A�@���L�L���i���|�����j�^��i�P�|�i���^���j^2�j�E�E�E�C
�@�B�ƇC�̂��L�L�͓������Ȃ���Ȃ�Ȃ�����A��r���邱�Ƃɂ��A
�@�����i���{���j�^�i�P�{�����^���O2�j
�ƂȂ�A�A�ł̍������x�������܂�܂��B
�ȏ�B