丂乽帪娫乿偲乽挿偝乿偵娭偟偰丄廬棃偐傜憡懳惈棟榑偺夝愢彂偵偍偄偰偝傑偞傑側愢柧偑側偝傟偰偒傑偟偨偑丄偦偺愢柧
偵偼榑棟揑偵柕弬偑偁傝傑偡丅埲壓偵偰巜揈偟傑偡丅
乵愢柧乶
丂傑偢帪娫偵娭偟偰偱偡偑丄偁傞姷惈宯偐傜丄偦偺宯偵懳偟偰偁傞堦掕懍搙偱塣摦偟偰偄傞暿偺姷惈宯傪尒傞偲丄
乵愢柧乶
丂傑偢帪娫偵娭偟偰偱偡偑丄偁傞姷惈宯偐傜丄偦偺宯偵懳偟偰偁傞堦掕懍搙偱塣摦偟偰偄傞暿偺姷惈宯傪尒傞偲丄
乽帪娫偑備偭偔傝偡偡傫偱偄傞傛偆偵尒偊傞乿偲摿庩憡懳榑偱偼愢柧偟傑偡丅
丂帪娫偑備偭偔傝偡偡傓偙偲偺寛掕揑徹嫆偲偟偰丄廬棃偐傜偁偘傜傟偰偒偨傕偺偵儈儏乕棻巕偺庻柦偺墑傃偺尰徾偑偁
丂帪娫偑備偭偔傝偡偡傓偙偲偺寛掕揑徹嫆偲偟偰丄廬棃偐傜偁偘傜傟偰偒偨傕偺偵儈儏乕棻巕偺庻柦偺墑傃偺尰徾偑偁
傝傑偡丅塅拡慄偐傜崅懍偱傆傝偦偦偖儈儏乕棻巕偼捠忢偺傕偺偵斾傋偰庻柦偑幚嵺偵墑傃傞偑丄偙傟偼崅懍偱塣摦偟
偰偄傞棻巕偺宯偺帪娫偑備偭偔傝偡偡傫偩徹嫆偱偁傞偲愢柧偝傟偰偒傑偟偨丅
偙偺愢柧偐傜偡傞偲丄乽帪娫偑備偭偔傝偡偡傫偱偄傞傛偆偵尒偊傞乿偲偄偆偺偼丄乬尒偊傞乭偺傒側傜偢偦偺宯偱偼幚嵺偵
偙偺愢柧偐傜偡傞偲丄乽帪娫偑備偭偔傝偡偡傫偱偄傞傛偆偵尒偊傞乿偲偄偆偺偼丄乬尒偊傞乭偺傒側傜偢偦偺宯偱偼幚嵺偵
帪娫偑備偭偔傝恑傫偩偐傜偱偁傞偲偄偆偙偲偵側傝丄尒偐偗偱偼側偔丄幚幙揑側帪娫偺抶傟偑偁傞偲偄偆偙偲偵側傝傑
偡乮側偤側傜丄幚嵺偵庻柦偑墑傃偨偺偱偡偐傜乯丅摿庩憡懳榑偺惓偟偝傪帵偡徹嫆偺堦偮偲偟偰愄偐傜偁偘傜傟偰
偒偨偺偼偛懚抦偺捠傝偱偡丅
丂偮偓偵乬挿偝乭傪峫偊偰傒傑偡丅
偁傞姷惈宯偐傜丄偦偺宯偵懳偟偰偁傞堦掕懍搙偱塣摦偟偰偄傞暿偺姷惈宯傪尒傞偲丄乽暔懱偺挿偝偑弅傫偱偄傞傛偆偵
丂偮偓偵乬挿偝乭傪峫偊偰傒傑偡丅
偁傞姷惈宯偐傜丄偦偺宯偵懳偟偰偁傞堦掕懍搙偱塣摦偟偰偄傞暿偺姷惈宯傪尒傞偲丄乽暔懱偺挿偝偑弅傫偱偄傞傛偆偵
尒偊傞乿偲憡懳榑偱偼愢柧偟傑偡丅
丂偙偙偱婏柇側偙偲偵婥晅偒傑偡丅
丂乬挿偝乭偺曽偼丄帪娫偲堘偭偰乽幚嵺偵挿偝偑弅傫偩徹嫆偼偙傟偱偁傞両乿偲偄偆幚椺偑側偤偐堦偮傕曬崘偝傟偰
偄側偄偺偱偡乮偙偺揰偼丄屻摗嫵庼傕挊彂乽憡懳惈棟榑偺撲偲媈栤乿偺拞偱偨偟偐巜揈偟偰偄傑偟偨乯丅帪娫偱抶傟偑
偁傞側傜偽丄挿偝偵娭偟偰傕丄乽恑峴曽岦偵弅傫偩暔懱偑敪尒偝傟偨両乿偲偄偆僯儏乕僗偑偁偭偰傕傛偝偦偆偵巚偄傑偡偑丄
暦偄偨偙偲偑偁傝傑偣傫丅
丂偙傟偼偳偆偄偆偙偲偱偟傚偆偐丠
丂偙傟偼偳偆偄偆偙偲偱偟傚偆偐丠
帪娫偼幚嵺偵抶傟偑娤應偝傟偰偄傞偺偵丄挿偝偺曽偼偁偔傑偱尒偐偗偱嵪傑偣偽傛偄偲偄偆偙偲側偺偱偟傚偆偐丠
丂偟偐偟丄偙傟偼偍偐偟側偙偲偱偡丅
丂憡懳榑偺榑棟揥奐傪峫偊傞偲丄帪娫偲挿偝乮嬻娫乯偼丄杮幙揑偵嬫暿偟偰偁偮偐偭偰偄側偄偺偱丄忋偺傛偆偵
丂偟偐偟丄偙傟偼偍偐偟側偙偲偱偡丅
丂憡懳榑偺榑棟揥奐傪峫偊傞偲丄帪娫偲挿偝乮嬻娫乯偼丄杮幙揑偵嬫暿偟偰偁偮偐偭偰偄側偄偺偱丄忋偺傛偆偵
堦曽偼幚幙揑偵曄壔偑偁傞偺偵丄傕偆堦曽偼乬尒偐偗乭偵偡偓側偄側偳偲偄偆偙偲偼婲偙傞偼偢偑偁傝傑偣傫丅
丂椉曽偲傕乬幚幙偺曄壔偑偁傞乭偐傑偨偼椉曽偲傕乬尒偐偗偵偡偓側偄乭偲偄偆偙偲側傜偽榖偼傢偐傞偺偱偡偑丄堦曽
丂椉曽偲傕乬幚幙偺曄壔偑偁傞乭偐傑偨偼椉曽偲傕乬尒偐偗偵偡偓側偄乭偲偄偆偙偲側傜偽榖偼傢偐傞偺偱偡偑丄堦曽
偼乽幚幙揑丒丒乿偲偄偄丄傕偆堦曽偼乽尒偐偗偵偡偓側偄乿側偳偲偄偆偺偼榑棟揑側嬝偑捠偭偰偍傜偢丄摓掙庴偗
擖傟傞偙偲偼偱偒傑偣傫丅
丂憡懳惈棟榑偺嫵壢彂摍偱丄帪娫偲嬻娫偺愢柧傪偦傟偧傟撈棫偵撉傫偱偄傞撪偵偼婥偯偐側偐偭偨偙偲偑丄
偙偆偟偰俀偮傪暲傋傞偲丄廳戝側栤戣傪傆偔傫偱偄傞偙偲偑傢偐傞偺偱偡丅
丂摿庩憡懳惈棟榑偺寚娮偑傑偨堦偮業掓偟偨偲偄偊傞偱偟傚偆丅
愢柧廔傢傝
丂崱夞巜揈偟偨偙偺柕弬傪乽帪娫偲挿偝偵偍偗傞旕懳徧偺柕弬乿偲柤偯偗丄崱屻偝傑偞傑側応強偱媍榑偝傟傞偙偲傪
丂崱夞巜揈偟偨偙偺柕弬傪乽帪娫偲挿偝偵偍偗傞旕懳徧偺柕弬乿偲柤偯偗丄崱屻偝傑偞傑側応強偱媍榑偝傟傞偙偲傪
婓朷偟傑偡丅

俀侽侽1乛俉乛俀俉
丂丂丂丂丂丂丂丂亙侾亅俀丏岝帪寁偺峫嶡偐傜憡懳榑偵偍偗傞帪娫榑偺娫堘偄傪偝偖傞亜
帪娫偵偮偄偰偼乽帪娫丒嬻娫偺斀徣偲暔棟妛偺怴偟偄婎杮岞棟偺採埬乿偱傕徻偟偔榑偠傑偟偨偑丄暿偺帇揰偐傜傒偰
丂丂丂丂丂丂丂丂亙侾亅俀丏岝帪寁偺峫嶡偐傜憡懳榑偵偍偗傞帪娫榑偺娫堘偄傪偝偖傞亜
帪娫偵偮偄偰偼乽帪娫丒嬻娫偺斀徣偲暔棟妛偺怴偟偄婎杮岞棟偺採埬乿偱傕徻偟偔榑偠傑偟偨偑丄暿偺帇揰偐傜傒偰
傕憡懳惈棟榑偺帪娫榑偵偼巚峫忋偺岆傝偑懚嵼偟偰偄傑偡丅傾僀儞僔儏僞僀儞偺帪娫榑偼僨僞儔儊偱偁傞偲偄偊傞偺偱
偡偑丄廳戝側揰偱偡偺偱丄壓婰偵偰巜揈偟傑偟偨丅
| 乵梫栺乶 丂傑偢偼偠傔偵梫揰偩偗弎傋傑偡偲丄晛曊揑側帪娫偺棳傟傪岝帪寁偲偄偆傕偺偱戙懼偟偰偟傑偭偨偙偲偑憡懳惈棟榑偵偍 偗傞寛掕揑側娫堘偄偱偁傝傑偟偨丅岝帪寁偺恑傒偼帪娫偦偺傕偺偱偼側偄偵傕偐偐傢傜偢丄傾僀儞僔儏僞僀儞偼乽岝帪寁 偺恑傒亖晛曊揑帪娫偺棳傟乿偲嫮堷偵僀僐乕儖偱寢傫偱偟傑偭偨偙偲偑丄俀侽悽婭暔棟妛傪崻掙偐傜岆偭偨摴傊偲摫偄偰 偟傑偭偨尨場偺堦偮偲偄偊傞偺偱偡丅 |
埲壓徻偟偔愢柧偟傑偡丅
乵愢柧乶
丂憡懳惈棟榑偱偼丄岝帪寁偑抶傟傟偽偦偺宯慡懱偺晛曊揑側帪娫傑偱抶傟傞偲庡挘偟傑偡丅岝帪寁偑抶傟傞偲丄偦偺
乵愢柧乶
丂憡懳惈棟榑偱偼丄岝帪寁偑抶傟傟偽偦偺宯慡懱偺晛曊揑側帪娫傑偱抶傟傞偲庡挘偟傑偡丅岝帪寁偑抶傟傞偲丄偦偺
宯撪偺岝帪寁偺傒側傜偢丄偤傫傑偄帪寁側偳偺婡夿幃帪寁傗怳傝巕帪寁丄寢徎偺怳摦傪棙梡偡傞僋僆乕僣帪寁丄偼偨
傑偨嵒帪寁傑偱傕抶傟丄偝傜偵惗偒暔偺怱憻偺屰摦傕惉挿偺搙崌偄傑偱傕側偵傕偐傕抶傟傞偲愢柧偟傑偡丅
丂偟偐偟丄偦傫側偙偲偼偁傝傑偣傫丅
丂岝帪寁偺恑峴偑偍偔傟偨傜丄側偤椡妛揑偵摦偔婡夿幃帪寁傑偱抶傟偼偠傔側偗傟偽側傜側偄偺偐丠抶傟傞棟桼偑傑偭
丂岝帪寁偺恑峴偑偍偔傟偨傜丄側偤椡妛揑偵摦偔婡夿幃帪寁傑偱抶傟偼偠傔側偗傟偽側傜側偄偺偐丠抶傟傞棟桼偑傑偭
偨偔側偄偺偱偡丅
丂偦傟偼偨偩岝帪寁偑抶傟偰偄傞偩偗偱偁傝丄偦傟埲忋偺堄枴偼偁傝傑偣傫丅岝帪寁偑抶傟偨忬懺偲偄偆偺偼丄岝
丂偦傟偼偨偩岝帪寁偑抶傟偰偄傞偩偗偱偁傝丄偦傟埲忋偺堄枴偼偁傝傑偣傫丅岝帪寁偑抶傟偨忬懺偲偄偆偺偼丄岝
乮揹帴攇乯偑梋寁側嫍棧傪偡偡傓偨傔偵傛傝懡偔偺帪娫偑偐偐偭偨忬懺傪偄偆偺偱偡偑丄偦傫側傆偆偵岝偺塣摦偑曄壔
偟偨傜丄側偤宯偺晛曊揑帪娫傑偱抶傟傞偙偲偵側傞偺偐丄偠偮偼偦偺崻嫆偑側偵傕側偄偺偱偡丅
丂岝帪寁偵崌傢偣偰婡夿幃帪寁丄僋僆乕僣帪寁傑偱抶傟偼偠傔傞偙偲側偳側偄偟丄傑偟偰怱憻偺屰摦傑偱備偭偔傝偵側傞
丂岝帪寁偵崌傢偣偰婡夿幃帪寁丄僋僆乕僣帪寁傑偱抶傟偼偠傔傞偙偲側偳側偄偟丄傑偟偰怱憻偺屰摦傑偱備偭偔傝偵側傞
偙偲傕偁傝傑偣傫丅愄偼丄悈帪寁丄儔儞僾帪寁丄儘僂僜僋帪寁丄慄崄帪寁丄崄帪寁側偳偝傑偞傑側帪寁偑偁偭偨偺偱偡傛丅
丂偙偙偱丄岝帪寁偲偼側偵偐傪偼偭偒傝偝偣偰偍偒傑偟傚偆丅
乽帪娫丄嬻娫丄偦偟偰塅拡乿乮屗揷惙榓挊丂娾攇彂揦乯偐傜堷梡偟傑偡丅
丂偙偙偱丄岝帪寁偲偼側偵偐傪偼偭偒傝偝偣偰偍偒傑偟傚偆丅
乽帪娫丄嬻娫丄偦偟偰塅拡乿乮屗揷惙榓挊丂娾攇彂揦乯偐傜堷梡偟傑偡丅
| 岝帪寁 丂乽堦掕偺嫍棧偵偍偄偨暯峴側僯枃偺嬀偺娫傪墲暅偡傞岝偺僷儖僗偑偁偭偨偲偡傞偲丄偙傟偼揹帴尰徾傪梡偄 偨嵟傕娙扨側帪寁偲偟偰巊偊傑偡乮壓恾俙乯丅偙傟傪岝帪寁偲偄偆偙偲偵偟傑偟傚偆丅岝偺僷儖僗偑堦曽偺嬀偐傜 懠曽偺嬀傊峴偔帪娫傪乽僠僋乿偲悢偊丆婣傞帪娫傪乽僞僋乿偲悢偊傟偽丄岝帪寁偺僠僋丒僞僋偱帪娫偑應傟傑偡丅偙 偆偄偆帪寁傪峫偊傞偲丄憡懳惈棟榑傪媍榑偡傞偺偵偨偄傊傫曋棙偱偡丅偡傋偰偺暔棟尰徾偼丄乮偨偲偊偽嵨傪偲 傞偲偄偭偨尰徾傕娷傔偰乯揹帴婥偺朄懃偵偮傟偰丄偟偨偑偭偰岝帪寁偺帪娫偵偮傟偰恑峴偟傑偡丅偟偨偑偭偰 岝帪寁偺帵偡帪娫偼摿暿側帪娫偱偼側偔偰丄晛曊揑側帪娫傪戙昞偡傞傕偺偱偡丅乿 |
憡懳惈棟榑偵偍偗傞帪娫偲偄偆傕偺偑尒帠偵愢柧偝傟偰偄傑偡丅
偟偐偟丄愭偵傕弎傋偨傛偆偵忋婰偺撪梕偼娫堘偭偰偄傑偡丅
丂乽偡傋偰偺暔棟尰徾偼丄乮偨偲偊偽嵨傪偲傞偲偄偭偨尰徾傕娷傔偰乯揹帴婥偺朄懃偵偮傟偰丄偟偨偑偭偰岝帪寁偺帪娫
偵偮傟偰恑峴偟傑偡丅乿側偳偲側偤尵偊傞偺偐丠
偦偆尵偊傞崻嫆傪壗傕偁偘偰偄側偄偵傕偐偐傢傜偢丄嫮堷偵擔忢偺晛曊揑側帪娫偵寢傃晅偗偰偟傑偭偰偄傞偺偑傢偐
傝傑偡乮懠偺慡偰偺嫵壢彂偱傕偦偆偱偡偑乯丅揤懱偺塣峴偼丄側傫偺椡偵傛偭偰塣峴偟偰偄傞偺偐丠嵒帪寁偼側傫偺椡
偵傛偭偰摦偄偰偄傞偲偄偆偺偱偟傚偆偐丠
丂摦偄偰偄傞宯偱偼壓偺恾俛偺傛偆偵岝偼恑峴偟乮仏乯丄抧忋偐傜傒偨傜偙偺帪寁偼備偭偔傝偡偡傫偱偄傞傛偆偵尒偊傞偱
丂摦偄偰偄傞宯偱偼壓偺恾俛偺傛偆偵岝偼恑峴偟乮仏乯丄抧忋偐傜傒偨傜偙偺帪寁偼備偭偔傝偡偡傫偱偄傞傛偆偵尒偊傞偱
偟傚偆偑丄偟偐偟偙傟偑婡夿幃帪寁丄嵒帪寁丄擔帪寁丄恖娫偺惉挿摍偵側傫傜塭嬁傪梌偊傞傕偺偱側偄偙偲傕傑偨柧敀側
偙偲偱偡丅
丂抧忋偐傜傒偰傕丄儘働僢僩偺拞偺婡夿幃帪寁偺恑峴偼抧忋偺傕偺偲傑偭偨偔摨偠偱偁傞偟丄傑偨儘働僢僩拞偺恖偺怱憻偺
丂抧忋偐傜傒偰傕丄儘働僢僩偺拞偺婡夿幃帪寁偺恑峴偼抧忋偺傕偺偲傑偭偨偔摨偠偱偁傞偟丄傑偨儘働僢僩拞偺恖偺怱憻偺
屰摦傕抧忋偲側傫傜曄傢傝偁傝傑偣傫丅幚嵺偼抧忋偐傜傒偨傜岝帪寁偑抶傟傞偲偄偆偩偗偺偙偲丄偨偩偦傟偩偗偺偙偲側
偝偄丅
丂忋婰偺杮偱偼丄恾俙偺岝帪寁偑抧忋偺娤應幰偺帪寁丄恾俛偺岝帪寁偑儘働僢僩偵偺偭偨岝帪寁偺塣峴偲偟偰愢柧偝傟
丂忋婰偺杮偱偼丄恾俙偺岝帪寁偑抧忋偺娤應幰偺帪寁丄恾俛偺岝帪寁偑儘働僢僩偵偺偭偨岝帪寁偺塣峴偲偟偰愢柧偝傟
偰偄傑偡丅
忋婰偺杮偱偼偝傜偵
忋婰偺杮偱偼偝傜偵
乽岝僷儖僗偑嬀偺娫傪墲暅偡傞娫偵丄抧忋娤應幰偐傜傒傟偽嬀偼儘働僢僩偲堦弿偵墶偵摦偒傑偡偐傜丄儘働僢僩偑巭傑偭
偰偄傞偲偒傛傝傕岝僷儖僗偼幬傔偵挿偄嫍棧傪摨偠懍偝偱們偱恑傑側偗傟偽側傝傑偣傫丅偙傟偼抧忋偺娤應幰偐傜尒傞偲丄
憱偭偰偄傞儘働僢僩偺帪寁偺曽偑備偭偔傝偲帪傪崗傓偙偲傪堄枴偟傑偡丅偙傟偑塣摦偵傛傞帪寁偺抶傟偲屇偽傟傞尰徾偱
偡丅偙傟偼傕偪傠傫儘働僢僩偵尷傝傑偣傫丅峲嬻婡傗揹幵偵忔偣偨帪寁傕丄抧忋偵偍偄偨帪寁偵斾傋傞偲備偭偔傝帪傪崗傓
偺偱偡丅乿偲婰弎偝傟偰偄傑偡丅
丂偛傑偐偝傟偰偼偄偗側偄偺偼丄乽丒丒抧忋偵偍偄偨帪寁偵斾傋傞偲備偭偔傝帪傪崗傓偺偱偡丅乿偲偄偆暥偱偡丅偙偙偱傕丄岝
丂偛傑偐偝傟偰偼偄偗側偄偺偼丄乽丒丒抧忋偵偍偄偨帪寁偵斾傋傞偲備偭偔傝帪傪崗傓偺偱偡丅乿偲偄偆暥偱偡丅偙偙偱傕丄岝
帪寁偺帪娫傪丄晛曊揑側帪娫偺棳傟偡側傢偪帪偺崗傒偵偙偭偦傝偲抲偒姺偊傛偆偲偄偆堄恾偑撉傒偲傟傞偙偲偱偡丅
丂偙傟偼偡傋偰偺憡懳榑偺嫵壢彂偵嫟捠偟偨愢柧偱偁傝丄岝帪寁偑恾俙偐傜恾俛偺傛偆偵曄傢傞偐傜偦偺宯偺帪娫傑偱
丂偙傟偼偡傋偰偺憡懳榑偺嫵壢彂偵嫟捠偟偨愢柧偱偁傝丄岝帪寁偑恾俙偐傜恾俛偺傛偆偵曄傢傞偐傜偦偺宯偺帪娫傑偱
抶傟偼偠傔傞丄偡側傢偪丄岝帪寁偑抶傟傟偽偦偺宯偺婡夿幃帪寁丄嵒帪寁偐傜惗暔偺怱憻偺屰摦丄恖偺惉挿偵偄偨傞
傑偱偡傋偰偑抶傟傞偲庡挘偡傞丅
傑偭偨偔傓偪傖偔偪傖側愢柧偱偡丅岝偲偄偆揹帴攇偺嫇摦偑宯偺偡傋偰偺塣摦傪婯掕偟偨傝偟側偄丅憡懳榑偺杮傪撉
傓嵺偼丄偙偺揰傪廫暘拲堄偟偰撉傫偱偔偩偝偄丅
丂俛恾偺尰徾側偳丄抧忋偐傜傒偨傜乽岝偑偁偺傛偆偵塣摦偟偰偄傞偺偩側乿偲偄偆堄枴偱偟偐側偔丄杮棃揑側帪娫偲偼慡偔
丂俛恾偺尰徾側偳丄抧忋偐傜傒偨傜乽岝偑偁偺傛偆偵塣摦偟偰偄傞偺偩側乿偲偄偆堄枴偱偟偐側偔丄杮棃揑側帪娫偲偼慡偔
柍娭學側尰徾偱偁傞偲偄偆偙偲偑戝帠側億僀儞僩偱偡丅

丂帪娫偲偼恖娫偑峫偊偩偟偨奣擮偱偁傝丄偦傟偼乽岝偱傕偭偰掕媊偝傟側偗傟偽側傜側偄乿偲偄偭偨戙暔偱偼偁傝傑偣傫丅
岝偱傕偭偰帪娫偲偄偆傕偺傪掕媊偟偰偟傑偭偨偑偨傔偵丄帪娫偼岝偲偄偆暔棟揑幚懱偺惈幙偵偑傫偠偑傜傔偵敍傜傟傞偲
偄偆晄帺桼嬌傑傝側偄帠懺偵敪揥偟偰偟傑偭偨偺偱偡丅
丂憡懳惈棟榑偱偼帪娫傪傑傞偱幚懱偺傛偆偵偁偮偐偭偰偄傑偡偑丄偦傟偼岝偱傕偭偰帪娫傪掕媊偟偰偟傑偭偨偙偲偐傜偺
丂憡懳惈棟榑偱偼帪娫傪傑傞偱幚懱偺傛偆偵偁偮偐偭偰偄傑偡偑丄偦傟偼岝偱傕偭偰帪娫傪掕媊偟偰偟傑偭偨偙偲偐傜偺
摉慠偺婣寢偩偭偨傢偗偱偡丅
丂尰戙暔棟妛偱宯偛偲偵屌桳偺帪娫傪峫偊側偗傟偽側傜側偄偲偄偆偍偐偟偐偙偲偵側偭偰偄傞偺傕丄傕偲傪偨偩偣偽傾僀
丂尰戙暔棟妛偱宯偛偲偵屌桳偺帪娫傪峫偊側偗傟偽側傜側偄偲偄偆偍偐偟偐偙偲偵側偭偰偄傞偺傕丄傕偲傪偨偩偣偽傾僀
儞僔儏僞僀儞偑帪娫傪彑庤偵柍棟傗傝岝偵寢傃偮偗偨偙偲偑尨場偟偰偄傑偡丅
岝傪巊偆偩偗側傜傑偩嵾偼愺偐偭偨偺偱偡偑乮偦傟傕儈僗偱偡偑乯丄偦傟傪乽摿庩憡懳惈尨棟乿偲乽岝懍搙晄曄偺尨棟乿偲
岝傪巊偆偩偗側傜傑偩嵾偼愺偐偭偨偺偱偡偑乮偦傟傕儈僗偱偡偑乯丄偦傟傪乽摿庩憡懳惈尨棟乿偲乽岝懍搙晄曄偺尨棟乿偲
偄偆屳偄偵柕弬偟偨尨棟偺忋偵懪偪棫偰偨傕偺偱偡偐傜丄憡懳惈棟榑偺帪娫偼搙傪偙偊偰偍偐偟側傕偺偵側偭偰偟傑
偭偨丅
丂偝傜偵丄偦偺偍偐偟側帪娫奣擮傪梡偄偰丄挿偝乮嬻娫乯傪掕媊偟偨傕偺偩偐傜丄嬻娫偺曽傑偱偍偐偟側偙偲偵側傝丄乽偙偭
偪偱偼弅傑側偄偑丄偁偭偪偺宯偐傜尒傟偽弅傫偱尒偊傞丅乿側偳偲偄偆婏柇側榖偑傑偐傝捠傞傛偆偵側偭偰偟傑偭偨丅
丂帪娫偲偄偆偺偼恖娫偵偲偭偰傢偐傝偵偔偄傕偺偺堦偮偱偡偺偱丄岝偲偄偆堦尒棟偵偐側偭偨傛偆偵尒偊傞傕偺偱愢柧
丂帪娫偲偄偆偺偼恖娫偵偲偭偰傢偐傝偵偔偄傕偺偺堦偮偱偡偺偱丄岝偲偄偆堦尒棟偵偐側偭偨傛偆偵尒偊傞傕偺偱愢柧
偝傟傞偲丄偩傟傕乽偦傫側傕偺偐丒丒丒乿偲偛傑偐偝傟偰偟傑偭偨偺傕柍棟偼側偄偲巚偄傑偡偑丅
丂偱偼傾僀儞僔儏僞僀儞偑側偤帪娫傪岝偱傕偭偰掕媊偟側偗傟偽側傜側偐偭偨偺偐丅
侾俋侽侽擭弶摢摉帪丄僄乕僥儖偑偳偆傗偭偰傕敪尒偝傟側偄棟桼乮愨懳宯偑偄偐側傞庤抜傪傕偪偄偰傕尒偮偐傜側偄棟桼乯
丂偱偼傾僀儞僔儏僞僀儞偑側偤帪娫傪岝偱傕偭偰掕媊偟側偗傟偽側傜側偐偭偨偺偐丅
侾俋侽侽擭弶摢摉帪丄僄乕僥儖偑偳偆傗偭偰傕敪尒偝傟側偄棟桼乮愨懳宯偑偄偐側傞庤抜傪傕偪偄偰傕尒偮偐傜側偄棟桼乯
傪傾僀儞僔儏僞僀儞偼偳偆偟偰傕扨弮側尨棟偐傜摫偒偨偐偭偨偐傜偲巚傢傟傑偡丅
摉帪丄僄乕僥儖偺栤戣偼暔棟妛偺戝栤戣偱偁傝丄僄乕僥儖偑尒偮偐傜側偄偙偲丄傑偨尒偮偐傜側偄偙偲偵懳偡傞偆傑偄
棟桼晅偗偑偱偒側偄偙偲偵暔棟妛幰偼戝偒側壵棫偪傪姶偠偰偄傑偟偨丅
丂偦偙偵镈憉偲搊応偟偨傾僀儞僔儏僞僀儞偲偄偆堦惵擭偑丄乽摿庩憡懳惈尨棟乿偲乽岝懍搙晄曄偺尨棟乿傪梡偄帪娫偺
掕媊傪曄峏偡傞偲偄偆傂偹傝媄傪壛偊傟偽丄儘乕儗儞僣偑摫偄偨偺偲偼堘偆曽朄偱丄儘乕儗儞僣曄姺偑摫偗傞偙偲偵婥
晅偒傑偟偨丅僄乕僥儖偲偄偆傕偺偵捈愙怗傟傞偙偲側偔丄儅僀働儖僜儞丒儌乕儗乕幚尡偺婏柇側寢壥傪丄偠偮偵偡偭偒傝偲
愢柧偟偰偟傑偭偨偺偱偡丅
偦偺偁傑傝偵娙寜偱尒帠乮丠乯側夝寛偺偟曽偵丄暔棟妛幰偑偲傃偮偄偨偺偼丄摉帪偺忬嫷傪峫偊傟偽偆側偯偗傑偡丅
丂偟偐偟丄偙偺夝寛偺巇曽偼丄慡偔偺岆傝偩偭偨偺偱偡丅傾僀儞僔儏僞僀儞偼丄廳戝側儈僗傪偄偔偮傕斊偟傑偟偨丅
偦偺儈僗偵娭偟偰偼丄
偦偺懠偱徻偟偔弎傋傑偟偨偺偱偛棗偔偩偝偄丅
偲傕偐偔丄恖椶偼傾僀儞僔儏僞僀儞偺岻柇側愢柧偵尒帠偵閤偝傟偰偟傑偭偨丅偦偺偛傑偐偟傪尒敳偗側偐偭偨傢偗偱偡丅
丂摉帪側傜偲傕偐偔丄俀侾悽婭偺崱偵帄偭偰傕傾僀儞僔儏僞僀儞偺敪柧偟偨帪娫傪戝愗偵庣傝偮偯偗偰偄傞偺偱偡偐傜丄
偙偺尰忬偵偼尵梩傕偁傝傑偣傫丅偛偔娙扨偵尵偊偽丄憡懳榑偺帪娫偼丄乽愨懳宯側偳側偄丄慡偰偼憡懳偱偁傞乿傪惓摉
壔偡傞偨傔偵惗傒弌偝傟傑偟偨丅岝帪寁偺帪娫偲変乆偺帪娫偲偼側傫偺娭學傕偁傝傑偣傫丅
妛幰偼丄乽憡懳榑偺帪娫偙偦偑杮暔偺帪娫乿偺傛偆偵尵傢側偄偲懱嵸偑偮偐側偄偐傜丄偄傑偱傕偦偺傛偆偵尵偄偮偯
偗偰偄傞偩偗偱偡丅傕偪傠傫丄儘乕儗儞僣廂弅傕婾傝偱偡丅
丂憡懳榑偱偺帪娫偑変乆偺尰幚偺帪娫偲傑偭偨偔寢傃偮偐側偄偲偄偆偙偲偵婥偯偐偢偵尰戙傑偱偒偰偟傑偭偨
偙偲偼丄暔棟妛偺楌巎偵偍偗傞寛掕揑側儈僗偩偭偨偲偄傢偞傞傪偊傑偣傫丅
丂丂俀侾悽婭弶摢偵帄偭偰傕丄妛幰偼傑偩婥偯偐側偄丒丒丒丒丅
丂丂俀侾悽婭弶摢偵帄偭偰傕丄妛幰偼傑偩婥偯偐側偄丒丒丒丒丅

丂丂丂丂丂丂亙侾亅俁丏憡懳榑偺尨棟偵傂偦傓棟夝晄壜擻側榑棟揥奐傪柧傜偐偵偡傞亜
丂偙偙偱偼丄岝帪寁偵娭偡傞廬棃愢柧偺岆傝偲丄憡懳榑偺攋抅椺傪帵偟傑偡丅
乵愢柧乶
丂傑偢偼偠傔偵丄摿庩憡懳惈棟榑偺尨棟偲側偭偰偄傞乽摿庩憡懳惈尨棟乿偲乽岝懍搙晄曄偺尨棟乿傪婰偟傑偡丅
岝懍搙晄曄偺尨棟
嘆乽恀嬻拞偺岝偺懍偝偼岝尮偺塣摦忬懺偵傛傜偢堦掕偱偁傞丅乿
摿庩憡懳惈尨棟
嘇乽暔棟朄懃偼丄偡傋偰偺姷惈宯偵懳偟偰摨偠宍偱偁傜傢偝傟傞丅乿
丂傾僀儞僔儏僞僀儞偼丄偙偺嘆偲嘇傪巜摫尨棟偲偟偰嵦梡偟摿庩憡懳榑傪嶌傝忋偘傑偟偨丅
偲偙傠偱丄嘆偼嘇傪峫椂偵擖傟傞偲丄偮偓偺傛偆偵傕昞尰偝傟傑偡丅
岝懍搙晄曄偺尨棟偺暿昞尰
嘊乽偄偐側傞姷惈宯乮娤應幰乯偐傜尒偰傕丄岝偺懍偝偼堦掕抣們偱偁傞丅乿
丂偝偰丄乽岝懍搙晄曄偺尨棟乿偺幚尡揑徹嫆偲偟偰傛偔偁偘傜傟傞傕偺偵丄楢惎偐傜偺岝偺懍偝偺應掕偑偁傝傑偡丅
乽憡懳惈棟榑乿乮拞栰摕晇挊丂娾攇彂揦乯偵偼偮偓偺傛偆偵婰偝傟偰偄傑偡丅
丂偙偙偱偼丄岝帪寁偵娭偡傞廬棃愢柧偺岆傝偲丄憡懳榑偺攋抅椺傪帵偟傑偡丅
乵愢柧乶
丂傑偢偼偠傔偵丄摿庩憡懳惈棟榑偺尨棟偲側偭偰偄傞乽摿庩憡懳惈尨棟乿偲乽岝懍搙晄曄偺尨棟乿傪婰偟傑偡丅
岝懍搙晄曄偺尨棟
嘆乽恀嬻拞偺岝偺懍偝偼岝尮偺塣摦忬懺偵傛傜偢堦掕偱偁傞丅乿
摿庩憡懳惈尨棟
嘇乽暔棟朄懃偼丄偡傋偰偺姷惈宯偵懳偟偰摨偠宍偱偁傜傢偝傟傞丅乿
丂傾僀儞僔儏僞僀儞偼丄偙偺嘆偲嘇傪巜摫尨棟偲偟偰嵦梡偟摿庩憡懳榑傪嶌傝忋偘傑偟偨丅
偲偙傠偱丄嘆偼嘇傪峫椂偵擖傟傞偲丄偮偓偺傛偆偵傕昞尰偝傟傑偡丅
岝懍搙晄曄偺尨棟偺暿昞尰
嘊乽偄偐側傞姷惈宯乮娤應幰乯偐傜尒偰傕丄岝偺懍偝偼堦掕抣們偱偁傞丅乿
丂偝偰丄乽岝懍搙晄曄偺尨棟乿偺幚尡揑徹嫆偲偟偰傛偔偁偘傜傟傞傕偺偵丄楢惎偐傜偺岝偺懍偝偺應掕偑偁傝傑偡丅
乽憡懳惈棟榑乿乮拞栰摕晇挊丂娾攇彂揦乯偵偼偮偓偺傛偆偵婰偝傟偰偄傑偡丅
塣摦偟偰偄傞岝尮
乽岝懍晄曄偺尨棟偵傛傞偲丄岝偺懍偝偼岝尮偺塣摦偵柍娭學偱偁傞丅偙偺尨棟偺専徹偼丄傑偢揤懱偺娤應偵傛偭偰峴
傢傟偨丅恀嬻拞偺惷巭岝尮偵傛傞岝懍傪們丄娤應幰偺曽傊懍偝倴偱塣摦偟偰偄傞岝尮偐傜偺岝偺懍偝傪們亴偲彂偒們亴亖們 亄倠倴偲偍偔丅俀偮偺惎偑屳偄偺傑傢傝傪夞揮偟偰偄傞擇廳惎偱偼丄堦曽偑抧媴偵嬤偯偄偰偄傞偲偒偼丄懠曽偺惎偼墦偞偐 偭偰偄傞丅偙傟傜偺惎偐傜偔傞岝傪娤應偟偨偲偙傠丄倠亙侾侽^-6偱偁傞偙偲偑抦傜傟偰偄傞丅乮搑拞棯乯 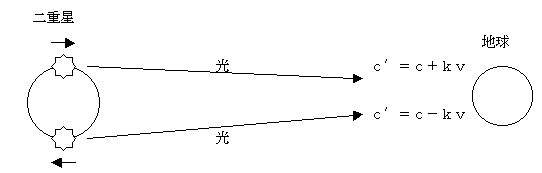 丂偙偺傛偆側偙偲偐傜丄倠亖侽偱偁傝丄岝懍搙晄曄偺尨棟偼惓偟偄偲峫偊傜傟傞丅乿 |
丂偙偺傛偆偵岝懍搙晄曄偺尨棟偺徹嫆偑偁偘傜傟偰偄傞傢偗偱偡偑丄偟偐偟彮偟峫偊傞偲傢偐傞捠傝丄偙傟偼乽岝偼愨懳
嬻娫傪捈恑偡傞乿偲偄偆儅僋僗僂僃儖偺峫偊偺惓偟偝傪妋擣偟偨傕偺偵側偭偰偄傞偵偡偓側偄偲偄偆偙偲偱偡丅岝偑愨懳宯
傪婎弨偵恑峴偡傞偙偲傪柧椖偵帵偟偰偄偰乮岝尮偺塣摦偵塭嬁傪庴偗側偄偙偲傪帵偟偰偄傞乯丄憡懳惈棟榑偺攋抅偺椺
偲偄偊傞偺偱偡丅
丂憡懳榑偼丄壓婰偺岝帪寁偺岝恑峴傪尒偰傕傢偐傞捠傝丄堦曽偱偼岝偼傑傞偱姷惈偺朄懃偵廬偆偐偺傛偆偵恑峴偡傞
偲庡挘偡傞棟榑乮岝尮偺塣摦偵塭嬁傪庴偗偰恑峴偡傞偺偩偲庡挘乯偱偡偺偱丄忋偺帠幚偑帺恎偺庡挘傪恀偭岦偐傜斲掕
偟偰偄傞偙偲傪峫偊傟偽丄憡懳榑偺撪晹柕弬偵婥偯偔偺偼梕堈偱偡丅
丂恾偺愢柧偼丄愨懳宯偺懚嵼傪巟帩偟偰偄傞偩偗偱偁傝丄偙偺楢惎偺寢壥偼嘊偺堄枴偺乽岝懍搙晄曄偺尨棟乿偺徹嫆
偵偼側偭偰偄側偄丅恾偱偼丄楢惎偑摦偒抧媴偑巭傑偭偰偄傞偲偄偆宍偲側偭偰偄偰丄偙傟偱偼嘊傪徹柧偡傞偙偲偼偱偒傑
偣傫丅
嘊傪徹柧偡傞偵偼丄抧媴偑嬤偯偄偰偄偔応崌偲墦偞偐傞応崌偺擇廳惎偐傜偺岝偺懍偝傪斾傋側偗傟偽側傜側偄偐傜偱偡丅
丂偙偺擇廳惎偐傜偺岝偺嫇摦偼丄憡懳榑抋惗埲慜偵奆偑儅僋僗僂僃儖曽掱幃偵娭偟偰擣幆偟偰偄偨乽揹帴攇偼愨懳宯
傪婎弨偵懍偝們偱憱傞乿偲偄偆揹帴攇偺嫇摦偦偺傕偺偲側偭偰偄傞偙偲偵拲栚偟偰偔偩偝偄丅
丂嘆偼尰戙暔棟妛偵偍偄偰傕惓偟偄傕偺偱偡丅偙傟偼儅僋僗僂僃儖偑揹帴婥妛傪姰惉偟偨偲偒偐傜奆偑擣幆偟偰偄偨偙偲
偱丄偙偺嘆偺昞尰偵偼丄側傫傜憡懳榑揑側梫慺偼偁傝傑偣傫丅岝懍搙晄曄偺尨棟偺惓偟偝傪徹柧偡傞偵偼丄嘆偱偼側偔丄
嘊偺曽傪偙偦幚徹偟側偗傟偽側傜側偄丅
丂偙偙傜偁偨傝偺嘆丄嘇丄嘊偺偐傜傑傝嬶崌傪傛偔棟夝偟偰偄側偄偲妛幰偺愢柧偵偛傑偐偝傟偰偟傑偄傑偡偺偱廫暘拲堄偟
偰偔偩偝偄丅
丂忋偺擇廳惎偺帠幚偼丄乽岝偼愨懳宯傪婎弨偵岝懍們偱憱傞乿偲偄偆偙偲傪巟帩偟丄愨懳宯偺懚嵼傪嫮椡偵庡挘偡傞撪梕
偺傕偺偱偁偭偰丄偠偮偼摿庩憡懳榑傪斲掕偡傞幚椺偱偁偭偨偺偱偡丅
丂暔棟妛幰偼丄摿庩憡懳榑偺攋抅椺傪乽憡懳榑偺惓偟偝偺徹嫆乿偲偟偰嫵壢彂摍偱偁偘偮偯偗
偰偄傞傢偗偱偡丅
寢嬊丄暔棟妛幰偼丄憡懳榑偵偍偄偰嵟傕杮幙揑側嘊偺応崌偺徹嫆傪偁偘傛偆偵傕偁偘傜傟偢丄嘆偺惓偟偝傪庡挘偟偰丄
偛傑偐偡偟偐庤偑側偄忬懺側偺偱偡丅
丂偪側傒偵丄岝偑丄岝帪寁偺傛偆偵丄姷惈偺朄懃偵廬偭偨傛偆側恑峴傪偡傞傕偺偱偼側偔丄愨懳宯傪婎弨偵憱傞傕偺偱
偁傞偙偲偼丄偮偓偺椺偱傕幚徹偝傟偰偄傑偡丅
乵岝偑丄姷惈偺朄懃偵廬傢偢丄愨懳宯傪婎弨偵憱傞偙偲傪幚徹偟偨椺乶
丂摿庩憡懳榑偺尨棟偵偍偗傞婏柇側揰傪偝偖偭偰傒傑偡丅偙偙偱岝帪寁傪帩偪弌偟偰傒傑偟傚偆丅

丂恾俙偵偍偄偰丄姷惈宯S亴偵屌掕偝傟偨岝尮偐傜岝偑忋曽岦偵敪偣傜傟墲暅塣摦偟偰偄傞偲偟傑偡丅傕偆傂偲偮偺姷惈
宯S傕峫偊丄偄傑宯S亴偼宯S偵懳偟偰塃曽岦偵懍搙倴偱摦偄偰偄傞偲偟傑偡丅宯S偐傜挱傔傟偽丄岝偼恾俛偺傛偆偵幬傔
忋曽偺嬀傪捛偄偐偗傞傛偆偵塣摦偡傞偲憡懳榑偱偼庡挘偟傑偡丅
丂偙偙偱傕偟丄姷惈宯S傪愨懳宯偵偍偒偐偊傟偽偳偆偱偟傚偆偐丅儅僋僗僂僃儖曽掱幃偵傛傟偽岝偼愨懳宯傪捈恑偡傞偲
丂偙偙偱傕偟丄姷惈宯S傪愨懳宯偵偍偒偐偊傟偽偳偆偱偟傚偆偐丅儅僋僗僂僃儖曽掱幃偵傛傟偽岝偼愨懳宯傪捈恑偡傞偲
嫵偊傑偡偐傜恾B偺傛偆偵幬傔偵偼恑傑偢丄恀忋偵偄偔偙偲偵側傝嬀偵偼摉偨傜側偄帠懺偵側偭偰丄忋偺岝帪寁偺愢柧偼
偍偐偟偄偲偄偆偙偲偵側傝傑偡丅偟偐偟丄尰戙暔棟妛偱偼丄乽愨懳宯偲偄偆偺偼偁傝偊側偄乿偲側偭偰偄傑偡偐傜丄偦傫側夝庍
偼嫋偝傟偰偄傑偣傫丅
丂偲偙傠偑丄岝偼愨懳宯傪婎弨偵恑峴偡傞偙偲偼丄峲嬻婡偵搵嵹偝傟偰偄傞儗乕僓乕僕儍僀儘偵傛偭偰幚徹偝傟偰偄傑偡
偟丄傑偨忋偺擇廳惎傪傒偰傕柧傜偐偱偡丅愨懳宯偼幚嵼偟傑偡丅
丂偝偰岝帪寁偱偼丄寢嬊丄岝尮偐傜偺岝偼師偺恾侾乮乽憡懳惈棟榑乿乮拞栰摕晇挊丂娾攇彂揦乯偺恾乯偺傛偆偵恑峴偡傞偲
偄偆嬃偔傋偒偙偲傪尵偭偰偄傞偺偲摨偠偱偡丅

丂偙傟偼丄岝偼儃乕儖偲摨偠傛偆側恑峴傪偡傞偲庡挘偡傞傕偺偱偡偑丄偼偨偟偰岝乮揹帴攇乯偑尰幚偵偙傫側恑峴傪偡傞
傕偺側偺偐偳偆偐丅
丂岝偼杮摉偵偙傫側恑傒曽傪偡傞偺偱偟傚偆偐丠
丂憡懳惈棟榑傪昁巰偱庣傠偆偲偡傞暔棟妛幰偼丄岝偼愨懳偵偙偺傛偆偵恑峴偡傞偲庡挘偟傑偡丅
側偤側傜丄尰戙暔棟妛幰偼摿庩憡懳惈尨棟偲偄偆尨棟傪婃側偵庣傞昁梫偑偁傞偐傜偱偡丅傕偟丄枩偑堦丄岝偑忋偺傛
偆側恑峴傪偟側偄偲敾柧偟偨側傜偽丄傕偟忋偺曽岦偐傜偪傚偭偲偱傕僘儗偰恑傓偙偲偑敾柧偟偨側傜偽丄揹帴婥妛偩偗偼宯
偵傛偭偰婰弎偑嵎暿壔偝傟傞偙偲偵側偭偰丄乽慡偰偺暔棟棟榑偼偳傫側姷惈宯偱傕摨摍乿偲偄偆戝尨棟偑攋傟傞偙偲偵側
傝丄憡懳榑偺傒側傜偢丄尰戙暔棟偼憤曵傟偟偰偟傑偆偐傜偱偡丅
岝偼丄偠偮偼丄岝帪寁偺傛偆側恑峴偺巇曽傪偟側偄偺偱偡丅
偦偺棟桼傪弎傋傑偡丅
忋偺擇廳惎偱偺岝偺嫇摦傪尒偰偔偩偝偄丅岝偼丄岝尮偺塣摦偺塭嬁傪庴偗側偄偙偲偑幚徹偝傟偰偄傑偡丅
偟偐傞偵丄忋偺岝帪寁乮巚峫忋偺嶻暔両乯偱偼丄岝尮偺塣摦偺塭嬁傪庴偗偰乮傑傞偱姷惈偺朄懃偵廬偆傛偆偵乯恑峴偡傞
偲偟偰偄傞丅惓斀懳偱偡丅
丂埲忋傛傝丄岝帪寁偺岝偺嫇摦偼塕偱偁傞偲抐尵偱偒傞偐傜偱偡丅
憡懳惈棟榑偑戝塕偺嬻榑偱偁傞偙偲偑傢偐傞偱偟傚偆丅
丂岝帪寁偙偦丄岝懍搙晄曄偺尨棟偲摿庩憡懳惈尨棟傪嬶尰壔偟偨傕偺偱偁傝丄摿庩憡懳榑偺搚戜偱偁傞偙偲傪偟偭偐傝
偲擣幆偟偰偔偩偝偄丅
丂偦偟偰丄偦傟偑傾僀儞僔儏僞僀儞偺偲傫偱傕側偄媆嵩偐傜敪柧偝傟偨傕偺偱偁傞偙偲傪両

丂巹偑埲慜偐傜怱偺掙偱丄偽偔偤傫偲媈栤偵巚偭偰偄偨栤戣偑偁傝傑偡丅偳偺嫵壢彂偱傕媍榑偝傟偰偍傜偢丄傑偨崱夞
柧夣側尵梩偲偟偰偲傝弌偡偙偲偑偱偒傑偟偨偺偱丄偙偙偵怴偟偄僷儔僪僢僋僗偲偟偰採帵偟丄奆條偺堄尒傪栤偄偨偄偲巚偄
傑偡丅埲壓偱扨偵乭宯乭偲尵偭偨応崌偼丄偡傋偰乭姷惈宯乭傪堄枴偟傑偡丅
乵僷儔僪僢僋僗偺採帵乶

丂偄傑丄偁傞堦偮偺姷惈宯俵撪偱岝偑塃岦偒偵懍偝們偱恑傫偱偄傞偲偟傑偡丅
暔懱俙偼塃岦偒偵懍偝倴偱恑傫偱偍傝丄傑偨暔懱俛偼嵍岦偒偵懍偝倴偱恑傫偱偄傞偲偟傑偡丅
丂偄傑俙偲俛偼姷惈宯俵偺拞偺暔懱偱偡偐傜丄暔懱俙偵懳偡傞岝偺懍偝偼們亅v偱偁傝丄傑偨暔懱俛偵懳偡傞岝偺懍偝
偼們亄v偲側傝傑偡丅俵偲偄偆堦偮偺姷惈宯偺拞偱媍榑偟偰偄傞偙偲偱偡偐傜丄摉慠偙偆偄偆寁嶼偲側傝傑偡丅
丂偙傟偼丄暔懱俙偵懳偡傞岝偺憡懳懍搙偑們亅倴偵側傝丄暔懱俛偵懳偡傞岝偺憡懳懍搙偑們亄倴偲側傞偲偄偆偙偲偱偡丅
丂偙傟偼丄暔懱俙偵懳偡傞岝偺憡懳懍搙偑們亅倴偵側傝丄暔懱俛偵懳偡傞岝偺憡懳懍搙偑們亄倴偲側傞偲偄偆偙偲偱偡丅
偙偺応崌傪忬嫷嘆偲偟傑偟傚偆丅
丂偄傑丄暔懱俙偲暔懱俛傪偦傟偧傟娤應幰俙丄娤應幰俛偵抲偒姺偊傞偲偟傑偡丅偡傞偲丄搑抂偵忬嫷偑曄傢偭偰偒傑偡丅
丂娤應幰傪偁傞暿宯偺戙昞幰偲峫偊傞偲丄岝懍搙晄曄偺尨棟偺揔梡偱偒傞強偲側傝丄娤應幰俙偵偲偭偰岝偺懍偝偼們偵
丂偄傑丄暔懱俙偲暔懱俛傪偦傟偧傟娤應幰俙丄娤應幰俛偵抲偒姺偊傞偲偟傑偡丅偡傞偲丄搑抂偵忬嫷偑曄傢偭偰偒傑偡丅
丂娤應幰傪偁傞暿宯偺戙昞幰偲峫偊傞偲丄岝懍搙晄曄偺尨棟偺揔梡偱偒傞強偲側傝丄娤應幰俙偵偲偭偰岝偺懍偝偼們偵
尒偊丄傑偨娤應幰俛偵偲偭偰傕們偲側傝傑偡丅偙偺応崌傪忬嫷嘇偲偟傑偟傚偆丅
丂偝偰忬嫷嘆偲忬嫷嘇傪斾傋偨応崌丄旕忢偵婏柇側偙偲偵婥偯偒傑偡丅
丂忬嫷嘆偱偼丄俙偲俛傪偁傞堦偮偺姷惈宯偺拞偵偁傞暔懱偲偟偰峫嶡偟傑偟偨丅堦曽丄忬嫷嘇偱偼俙偲俛傪娤應幰偲偄偆
丂偝偰忬嫷嘆偲忬嫷嘇傪斾傋偨応崌丄旕忢偵婏柇側偙偲偵婥偯偒傑偡丅
丂忬嫷嘆偱偼丄俙偲俛傪偁傞堦偮偺姷惈宯偺拞偵偁傞暔懱偲偟偰峫嶡偟傑偟偨丅堦曽丄忬嫷嘇偱偼俙偲俛傪娤應幰偲偄偆
棫応偱峫偊傑偟偨丅偳偪傜傕丄暔懱偱偁傞偵偼堘偄側偔堄幆傪傕偭偰偄傞偐傕偭偰偄側偄偐偺嵎偵偡偓傑偣傫丅
丂忬嫷嘆偱偼暔懱俙偐傜尒偨傜岝偼們亅倴偱憱偭偰偔傞傛偆偵尒偊丄暔懱俛偱偼們亄倴偱偔傞傛偆偵尒偊傞丅偲偙傠偑丄忬嫷嘇
丂忬嫷嘆偱偼暔懱俙偐傜尒偨傜岝偼們亅倴偱憱偭偰偔傞傛偆偵尒偊丄暔懱俛偱偼們亄倴偱偔傞傛偆偵尒偊傞丅偲偙傠偑丄忬嫷嘇
偺傛偆偵暔懱傪娤應幰偲偟偰偲傜偊偨搑抂丄偳偪傜偺娤應幰偵傕岝偼們偱傗偭偰偔傞傛偆偵尒偊傞丅
丂傑偭偨偔晄壜夝側榖偱偡丅
丂傑偭偨偔晄壜夝側榖偱偡丅
丂摓掙擺摼偱偒傞榖偱偼偁傝傑偣傫丅乽暔懱偐傜尒偨丒丒乿傕乽娤應幰偐傜尒偨丒丒乿傕杮幙揑偵摨偠偱偁傞偙偲偼柧傜偐
偩偐傜偱偡丅
偙偙偱丄憡懳榑幰偼偮偓偺傛偆偵斀榑偡傞偐傕偟傟傑偣傫丅
乽偄傗丄忋偺媍榑偼娫堘偭偰偄傞丅憡懳惈棟榑偵傛傟偽丄偳傫側暔懱偐傜傒偰傕岝偺懍偝偼們偵尒偊傞偺偩両乿偲丅
丂偟偐偟丄偦偆偱偟傚偆偐丅
丂忬嫷嘆偼堦偮偺宯撪偵偍偗傞暔懱偲岝偺塣摦偺娭學偲峫偊偰偄傑偡偺偱丄岝偵懳偡傞暔懱偺憡懳懍搙偼丄暔懱俙
偙偙偱丄憡懳榑幰偼偮偓偺傛偆偵斀榑偡傞偐傕偟傟傑偣傫丅
乽偄傗丄忋偺媍榑偼娫堘偭偰偄傞丅憡懳惈棟榑偵傛傟偽丄偳傫側暔懱偐傜傒偰傕岝偺懍偝偼們偵尒偊傞偺偩両乿偲丅
丂偟偐偟丄偦偆偱偟傚偆偐丅
丂忬嫷嘆偼堦偮偺宯撪偵偍偗傞暔懱偲岝偺塣摦偺娭學偲峫偊偰偄傑偡偺偱丄岝偵懳偡傞暔懱偺憡懳懍搙偼丄暔懱俙
偺応崌丄摉慠們亅倴偲側傝傑偡丅乽偦偺暔懱偺棫応偐傜尒偨偲偒偺懍搙乮暔懱偐傜尒偨懍搙乯乿偲偄偆偺偑丄暔棟妛偵偍偗
傞憡懳懍搙偺掕媊偩偐傜偱偡丅傛偭偰丄忬嫷嘆偱憡懳懍搙偑們亅倴傗們亄倴偵側傞偺偼丄傑偭偨偔帺慠側媍榑側偺偱偡丅
丂偟偐偟忬嫷嘇偺傛偆偵丄岝偲姷惈宯乮娤應幰乯偺娫偺娭學偲偟偰偲傜偊偨偲偒丄憡懳榑偺岝懍搙晄曄偺尨棟偵傛傟偽丄
丂偟偐偟忬嫷嘇偺傛偆偵丄岝偲姷惈宯乮娤應幰乯偺娫偺娭學偲偟偰偲傜偊偨偲偒丄憡懳榑偺岝懍搙晄曄偺尨棟偵傛傟偽丄
忬嫷嘇偼乮娤應幰傪暿偺偁傞宯偺戙昞幰偲峫偊傞偲乯娤應幰俙偵傕俛偵傕岝偼們偱恑傫偱偔傞傛偆偵尒偊傞偙偲偵側傞丅
拲堄丗憡懳榑偱乭娤應幰乭偲尵偭偨応崌偼丄乭偁傞姷惈宯偺戙昞幰乭乮偁傞偄偼乽偁傞姷惈宯偵惷巭偡傞嵗昗偺尨揰乿偲尵偭偰傕傛偄乯偲偄偆
拲堄丗憡懳榑偱乭娤應幰乭偲尵偭偨応崌偼丄乭偁傞姷惈宯偺戙昞幰乭乮偁傞偄偼乽偁傞姷惈宯偵惷巭偡傞嵗昗偺尨揰乿偲尵偭偰傕傛偄乯偲偄偆
丂丂丂丂堄枴傪傕偪傑偡丅
丂乽堦偮偺宯撪偺暔懱偲偟偰傒傟偽們亅倴偲側傝丄偦偺暔懱傪娤應幰乮暿宯偺戙昞幰乯偲尒曽傪曄偊偨偩偗偱們偵側傞乿側偳
偲偄偆偺偼丄傑偭偨偔柕弬偟偨榖偱偼偁傝傑偣傫偐丅乽恀幚偼偳偆偩偭偨丠乿偲屻偱暔懱孨偵暦偄偨傜偳偆摎偊傞偺偱偟傚偆丠
傑偝偵僷儔僪僢僋僗偑敪惗偟偰偄傞偺偱偡丅
乮尵傢偢傕偑側偺拲堄偱偡偑丄忬嫷嘆傕摉慠憡懳榑傪巊偭偰偺媍榑偱偡偺偱丄偙偺揰偼岆夝偟側偄偱偔偩偝偄乯
乮尵傢偢傕偑側偺拲堄偱偡偑丄忬嫷嘆傕摉慠憡懳榑傪巊偭偰偺媍榑偱偡偺偱丄偙偺揰偼岆夝偟側偄偱偔偩偝偄乯
丂摨偠堦恖偺恖偑丄堦偮偺暔棟尰徾傪們亅倴偲尒偨傝丄傑偨摨帪偵乮両乯們偲尒偨傝偡傞丅偙偺婏柇偝偼側傫側偺偐丄憡懳榑
偼尪妎徢忬偺棟榑側偺偱偟傚偆偐丠偙傫側偙偲偵側傞偺偼丄棟榑偑崻杮揑偵偍偐偟偄偙偲偺徹嫆偱偟傚偆丅
丂憡懳榑偵偍偄偰偼丄暔懱丄宯丄娤應幰偺嶰偮偑偠偮偵偁偄傑偄偵巊梡偝傟偰偒偨傛偆偵巚傢傟偰側傝傑偣傫丅
丂偙傫側偍偐偟側榖偵側傞偺傕丄乽偳傫側娤應幰偵傕岝偺懍偝偼們偱偁傞乿偲偄偆岝懍搙晄曄偺尨棟偑娫堘偭偰偄傞偐傜
偱偡丅傒側偝傑偼偳偆巚傢傟傑偡偐丠
丂偝傜偵丄崌惉懍搙偺娤揰偐傜傕怴偟偄僷儔僪僢僋僗傕尒弌偟傑偟偨丅崱夞偺僷儔僪僢僋僗偲崌傢偣偰峫偊偰傒偰偔偩偝偄丅
乵捛婰乶2002/11/9
丂忋偺僷儔僪僢僋僗偺暔懱A丄暔懱B傪丄恖A丄恖B偲偡傞曽偑傛傝暘偐傝傗偡偄僷儔僪僢僋僗偵側傞偙偲偵婥晅偒傑偟偨丅
傕偪傠傫丄忋婰偺傑傑偱傕偐傑偄傑偣傫偑丄暔懱A丄暔懱B傪丄恖A丄恖B偵抲偒姺偊偰峫偊偰傒偰偔偩偝偄丅
憡懳榑偺柕弬偑傛傝慛柧偵偁傇傝弌偝傟傞偙偲偱偟傚偆丅

俀侽侽侾乛俋乛侾係
丂丂丂丂丂丂亙侾亅俆丏岝懍搙晄曄偺尨棟偼丄愨懳嬻娫傪慜採偵偟偨傕偺偱偁傞亜
丂崱夞偼丄岝懍搙晄曄偺尨棟偼丄愨懳嬻娫傪慜採偲偟側偗傟偽夝庍偱偒側偄傕偺偱偁傞偙偲傪傑偢帵偟傑偡丅
丂偝傜偵丄乽摿庩憡懳惈尨棟乿偲乽岝懍搙晄曄偺尨棟乿偼屳偄偵柕弬偡傞傕偺偱偁傝丄偦偺擇偮傪梈崌偝偣傞偙偲偼偱偒側偄
丂丂丂丂丂丂亙侾亅俆丏岝懍搙晄曄偺尨棟偼丄愨懳嬻娫傪慜採偵偟偨傕偺偱偁傞亜
丂崱夞偼丄岝懍搙晄曄偺尨棟偼丄愨懳嬻娫傪慜採偲偟側偗傟偽夝庍偱偒側偄傕偺偱偁傞偙偲傪傑偢帵偟傑偡丅
丂偝傜偵丄乽摿庩憡懳惈尨棟乿偲乽岝懍搙晄曄偺尨棟乿偼屳偄偵柕弬偡傞傕偺偱偁傝丄偦偺擇偮傪梈崌偝偣傞偙偲偼偱偒側偄
偙偲傪柧傜偐偵偟傑偡丅(擇偮偺尨棟偑柕弬偡傞偙偲偼孍揷巵偑挊彂偺拞偱尵媦偝傟偰偄傑偡偑徹柧傑偱偼婰偝傟偰偄側偐偭偨偲巚偄傑偡
偺偱丄偙偙偱偼巹偑尒弌偟偨徹柧傪婰偟傑偟偨)
乵愢柧乶
傑偢乽岝懍搙晄曄偺尨棟乿偲乽摿庩憡懳惈尨棟乿傪偼偠傔偵彂偒傑偡偲偮偓偺傛偆偵側傝傑偡丅
岝懍搙晄曄偺尨棟嘥
嘆乽恀嬻拞偺岝偺懍偝偼丄岝尮偺塣摦忬懺偵柍娭學側堦掕抣們偱偁傞丅乿
摿庩憡懳惈尨棟
嘇乽偨偑偄偵摍懍搙塣摦傪偟偰偄傞偡傋偰偺姷惈宯偵偍偄偰丄偡傋偰偺婎杮揑暔棟朄懃偼丄傑偭偨偔摨偠宍偱
嘆乽恀嬻拞偺岝偺懍偝偼丄岝尮偺塣摦忬懺偵柍娭學側堦掕抣們偱偁傞丅乿
摿庩憡懳惈尨棟
嘇乽偨偑偄偵摍懍搙塣摦傪偟偰偄傞偡傋偰偺姷惈宯偵偍偄偰丄偡傋偰偺婎杮揑暔棟朄懃偼丄傑偭偨偔摨偠宍偱
昞偝傟丄偦傟傜偺姷惈宯偺側偐偐傜摿暿側傕偺傪慖傃弌偡偙偲偼偱偒側偄丅乿
丂傾僀儞僔儏僞僀儞偼丄偙偺嘆偲嘇傪婎杮揑側尨棟偲偟偰嵦梡偟摿庩憡懳惈棟榑傪嶌傝忋偘傑偟偨丅
偲偙傠偱丄嘇傪峫椂偵擖傟傞偲丄嘆偺岝懍搙晄曄偺尨棟偼偮偓偺傛偆偵傕昞尰偝傟傑偡丅
岝懍搙晄曄偺尨棟丂嘦
嘊乽偄偐側傞姷惈宯乮娤應幰乯偐傜尒偰傕丄岝偺懍偝偼堦掕抣們偱偁傞丅乿
乮仏乯忋偺嘆乣嘊偼乽憡懳惈棟榑偺峫偊曽乿乮嵒愳廳怣挊丂娾攇彂揦乯傪嶲峫偵偟傑偟偨丅
埲壓丄偙傟傜偺尨棟傪偔傢偟偔尒偰偄偒傑偡丅
変乆偼偄傑憡懳榑偺抋惗偡傞捈慜侾俋侽係擭偵棫偭偰偄傞偲偟傑偟傚偆丅偦偟偰傾僀儞僔儏僞僀儞偺峫嶡傪椻惷偵捛偭偰
丂傾僀儞僔儏僞僀儞偼丄偙偺嘆偲嘇傪婎杮揑側尨棟偲偟偰嵦梡偟摿庩憡懳惈棟榑傪嶌傝忋偘傑偟偨丅
偲偙傠偱丄嘇傪峫椂偵擖傟傞偲丄嘆偺岝懍搙晄曄偺尨棟偼偮偓偺傛偆偵傕昞尰偝傟傑偡丅
岝懍搙晄曄偺尨棟丂嘦
嘊乽偄偐側傞姷惈宯乮娤應幰乯偐傜尒偰傕丄岝偺懍偝偼堦掕抣們偱偁傞丅乿
乮仏乯忋偺嘆乣嘊偼乽憡懳惈棟榑偺峫偊曽乿乮嵒愳廳怣挊丂娾攇彂揦乯傪嶲峫偵偟傑偟偨丅
埲壓丄偙傟傜偺尨棟傪偔傢偟偔尒偰偄偒傑偡丅
変乆偼偄傑憡懳榑偺抋惗偡傞捈慜侾俋侽係擭偵棫偭偰偄傞偲偟傑偟傚偆丅偦偟偰傾僀儞僔儏僞僀儞偺峫嶡傪椻惷偵捛偭偰
偄偒丄憡懳榑偵偍偗傞峫嶡偺岆傝傪傒偨偄偲巚偄傑偡丅
丂乬懍偝乭偲偄偆偲偒偼丄偄偮傕乽壗偵懳偡傞懍偝偐丠乿偲偄偆偙偲偑栤戣偵側傝傑偡丅摴傪帪懍5倠倣乛倛偱曕偔丄偲偄偆偲偒偼丄
丂乬懍偝乭偲偄偆偲偒偼丄偄偮傕乽壗偵懳偡傞懍偝偐丠乿偲偄偆偙偲偑栤戣偵側傝傑偡丅摴傪帪懍5倠倣乛倛偱曕偔丄偲偄偆偲偒偼丄
抧柺偵懳偟偰偺懍偝傪偄偭偰偄傞傢偗偱偡丅偱偡偐傜丄嘆偼丄乽岝尮偺塣摦忬懺偵柍娭學偵丄懍偝偑堦掕抣們偲側傞傛偆
側摿暿側宯偑懚嵼偡傞偺偩乿偲偄偆偙偲傪嫮椡偵庡挘偟偰偄傞偲尵偄偐偊傞偙偲偑偱偒傑偡乮偙傟偼丄憡懳榑抋惗埲慜偺
儅僋僗僂僃儖曽掱幃偺夝庍偦偺傕偺偱偡両乯丅
丂傕偟偦偺傛偆側宯偑堦偮傕側偄側傜偽丄嘆偺庡挘傪偡傞偙偲帺懱柍堄枴偱偡偐傜丄嘆偼偦偆偄偆堄枴側偺偱偡丅偦偺
丂傕偟偦偺傛偆側宯偑堦偮傕側偄側傜偽丄嘆偺庡挘傪偡傞偙偲帺懱柍堄枴偱偡偐傜丄嘆偼偦偆偄偆堄枴側偺偱偡丅偦偺
宯偺悢偼丄堦偮偐擇偮偐丒丒偁傞偄偼傕偭偲偨偔偝傫偁傞偺偐抦傟側偄偑丄偲偵偐偔偦偺傛偆摿暿側宯偺懚嵼傪嘆偼庡
挘偟偰偄傞丅
丂偟偐偟丄傕偟懚嵼偡傞偲偡傟偽丄偦偺摿暿側宯偼偠偮偼堦偮偩偗側偺偩丄偲偄偆偙偲傪埲壓偵徹柧偟傑偡丅
乵徹柧乶
丂偄傑壖偵丄岝偺懍偝偑堦掕抣們偲側傞傛偆側摿暿側宯偲偟偰宯俙偑懚嵼偟偨偲壖掕偟傑偟傚偆丅
偄傑宯俛偼宯俙偵懳偟丄偁傞堦掕懍搙倴偱摦偄偰偄傞偲偟傑偡丅
壖掕偵傛傝丄宯俙偺嵗昗偵惷巭偟偨恖偐傜尒傞偲岝偼堦掕抣們偱恑傫偱尒偊傞偺偼柧傜偐偱偡丅偝偰丄宯俛偼宯俙偵懳
丂偟偐偟丄傕偟懚嵼偡傞偲偡傟偽丄偦偺摿暿側宯偼偠偮偼堦偮偩偗側偺偩丄偲偄偆偙偲傪埲壓偵徹柧偟傑偡丅
乵徹柧乶
丂偄傑壖偵丄岝偺懍偝偑堦掕抣們偲側傞傛偆側摿暿側宯偲偟偰宯俙偑懚嵼偟偨偲壖掕偟傑偟傚偆丅
偄傑宯俛偼宯俙偵懳偟丄偁傞堦掕懍搙倴偱摦偄偰偄傞偲偟傑偡丅
壖掕偵傛傝丄宯俙偺嵗昗偵惷巭偟偨恖偐傜尒傞偲岝偼堦掕抣們偱恑傫偱尒偊傞偺偼柧傜偐偱偡丅偝偰丄宯俛偼宯俙偵懳
偟偰堦掕懍搙偱摦偄偰偄傞偺偱偡偐傜丄宯俛撪偵惷巭偟偨恖偐傜岝傪傒傞偲丄偦偺懍偝偼摉慠們偲偼側傝傑偣傫丅傛偭偰
宯俛偼摿暿側宯偲偼側傝偊側偄偙偲偑傢偐傝傑偡丅
宯俙偵懳偡傞懍搙偑侽埲奜偺條乆側抣傪偲傞懠偺宯傪峫偊偰傕丄偦傟傜偺偄偐側傞宯傕乽摿暿側宯乿偲側傞偙偲偼側偄
偙偲偼偡偖偵傢偐傝傑偡丅
傛偭偰丄摿暿側宯偑擇偮埲忋懚嵼偡傞偙偲偼偁傝偊側偄丄傕偟偁傞偲偡傟偽丄偦傟偼偨偩堦偮偱偁傞丄偲偄偆偙偲偑徹柧
偝傟傑偟偨乮尵偆傑偱傕側偄偙偲偱偡偑丄偦偺愨懳宯偵惷巭偟偨悢妛揑側嵗昗宯偼柍悢偵愝掕偱偒傑偡乯丅
廔傢傝丅
丂嘆偼丄乽偩偨堦偮偺摿暿側宯偑偙偺悽偵偁傞偺偩乿偲丄偦偺懚嵼傪愊嬌揑偵庡挘偟偰偄傞丅
摉帪丄偦偺摿暿側宯偼丄愨懳嬻娫傑偨偼愨懳宯偲屇偽傟偰偄傑偟偨偐傜丄偙偙偱傕偦偺屇傃曽偵側傜偄傑偡偲丄嘆偼
丂嘆偼丄乽偩偨堦偮偺摿暿側宯偑偙偺悽偵偁傞偺偩乿偲丄偦偺懚嵼傪愊嬌揑偵庡挘偟偰偄傞丅
摉帪丄偦偺摿暿側宯偼丄愨懳嬻娫傑偨偼愨懳宯偲屇偽傟偰偄傑偟偨偐傜丄偙偙偱傕偦偺屇傃曽偵側傜偄傑偡偲丄嘆偼
愨懳嬻娫偺懚嵼傪嫮椡偵庡挘偟偰偄傞丅
嘆偼丄愨懳嬻娫偺懚嵼傪庡挘偟偰偄傞丅
嘇偼丄愨懳嬻娫偺懚嵼傪斲掕偟偰偄傞丅
丂偙偺傛偆偵尵偊傞偙偲偼丄偩傟偺栚偵傕柧傜偐偵側傝傑偟偨丅嘆偲嘇偼慡偔惓斀懳偺偙偲傪庡挘偟偰偄傞丅
丂偝偰丄摉帪偺棫応偱峫偊傞偲丄偙偺傛偆偵傑偭偨偔愜傝崌傢側偄擇偮偺尨棟傪嵦梡偟偰棟榑傪峔抸偟傛偆側偳偩傟傕
巚傢側偄偙偲側偳偡偖偵傢偐傝傑偡丅嘆偲嘇偼柕弬偟偰偄傞偺偱偡偐傜丅
丂偲偙傠偑丄堦恖傾僀儞僔儏僞僀儞偩偗偑堘偄傑偟偨丅
丂斵偼丄娙寜偐偮摑堦揑側宍幃偲偄偆傕偺偑堎忢側傎偳岲偒偩偭偨偺偱偟傚偆丅嘆偲嘇傪側傫偲偐梈崌偝偣偨偐偭偨丅
丂嘆偼儅僋僗僂僃儖曽掱幃偺惈幙傪昞尰偟偨傕偺丄嘇偼僯儏乕僩儞椡妛傪堄幆偟偨傕偺偲偄偊傑偡偑丄扨弮側尨棟
丂偲偙傠偑丄堦恖傾僀儞僔儏僞僀儞偩偗偑堘偄傑偟偨丅
丂斵偼丄娙寜偐偮摑堦揑側宍幃偲偄偆傕偺偑堎忢側傎偳岲偒偩偭偨偺偱偟傚偆丅嘆偲嘇傪側傫偲偐梈崌偝偣偨偐偭偨丅
丂嘆偼儅僋僗僂僃儖曽掱幃偺惈幙傪昞尰偟偨傕偺丄嘇偼僯儏乕僩儞椡妛傪堄幆偟偨傕偺偲偄偊傑偡偑丄扨弮側尨棟
偺偲偙傠偱丄偙偺俀偮傪宍幃偺忋偱摑堦揑偵昞尰偟偨偐偭偨偺偱偡丅宍幃偲偄偆傕偺偵堎忢偵偙偩傢偭偨偺偑傾僀儞僔儏
僞僀儞偱偟偨丅
丂嘆偲嘇偺梈崌偐傜惗傑傟偨嘊側偳丄偩傟偑尒偰傕岆傝側偺偼偁偒傜偐偱偡丅偟偐偟丄傾僀儞僔儏僞僀儞偼乽椡妛偺朄懃偼
丂嘆偲嘇偺梈崌偐傜惗傑傟偨嘊側偳丄偩傟偑尒偰傕岆傝側偺偼偁偒傜偐偱偡丅偟偐偟丄傾僀儞僔儏僞僀儞偼乽椡妛偺朄懃偼
偡傋偰偺姷惈宯偵丒丒乿偱偼側偔丄乽偡傋偰偺暔棟朄懃偼偡傋偰偺姷惈宯偵丒丒丒乿偲偳偆偟偰傕偟偨偐偭偨丅
嘆偲嘇側偳偩傟偑尒偰傕柕弬偟偰偄傞偟丄嘊側偳彫妛惗偑傒偰傕塕偲傢偐傝傑偡丅
偟偐偟丄嘊傪側傫偲偐惉棫偝偣偨偄丅偳偆偡傟偽偄偄偐丒丒丒丅
乽崲偭偨丅偄傗丄懸偰傛丅偦偆偩丅帪娫偲偼偦傕偦傕岝偲偄偆庤抜偱偟偐昞尰偱偒側偄偺偱偼側偄偐丠帪娫傪丄乽摿庩憡
嘆偲嘇側偳偩傟偑尒偰傕柕弬偟偰偄傞偟丄嘊側偳彫妛惗偑傒偰傕塕偲傢偐傝傑偡丅
偟偐偟丄嘊傪側傫偲偐惉棫偝偣偨偄丅偳偆偡傟偽偄偄偐丒丒丒丅
乽崲偭偨丅偄傗丄懸偰傛丅偦偆偩丅帪娫偲偼偦傕偦傕岝偲偄偆庤抜偱偟偐昞尰偱偒側偄偺偱偼側偄偐丠帪娫傪丄乽摿庩憡
懳惈尨棟乿偲乽岝懍搙晄曄偺尨棟乿傪婎慴偲偟丄岝傪巊偭偰掕媊偟捈偟偰傒傞偲丒丒丒
偍偍丄偁偺儘乕儗儞僣曄姺幃偑弌偰偔傞偱偼側偄偐両儘乕儗儞僣傜偺傛偆偵恖岺揑側壖愢傪愝偗偰摫偔曽朄傛傝丄偙偪傜
偍偍丄偁偺儘乕儗儞僣曄姺幃偑弌偰偔傞偱偼側偄偐両儘乕儗儞僣傜偺傛偆偵恖岺揑側壖愢傪愝偗偰摫偔曽朄傛傝丄偙偪傜
偺曽偑傛傎偳偡偭偒傝偟偰偄傞両愢摼椡傕偁傝偦偆偩丅乿
偲丄偙偺傛偆側宱堒傪傊偰丄桳柤側乽摦偄偰偄傞暔懱偺揹婥椡妛乿傪侾俋侽俆擭偵彂偄偨偲憐憸偝傟傑偡丅
帪娫偲偼傢偐傝偵偔偄傕偺偱偡丅
偦偺傢偐傝偵偔偄傕偺傪丄岝偱傕偭偰偁偺傛偆偵昞尰偝傟傞偲丄偩傟傕乽帪娫偭偰丒丒偦傫側傕偺側偺偐丒丒丒乿偲側偭偰偟傑偭偰
偲丄偙偺傛偆側宱堒傪傊偰丄桳柤側乽摦偄偰偄傞暔懱偺揹婥椡妛乿傪侾俋侽俆擭偵彂偄偨偲憐憸偝傟傑偡丅
帪娫偲偼傢偐傝偵偔偄傕偺偱偡丅
偦偺傢偐傝偵偔偄傕偺傪丄岝偱傕偭偰偁偺傛偆偵昞尰偝傟傞偲丄偩傟傕乽帪娫偭偰丒丒偦傫側傕偺側偺偐丒丒丒乿偲側偭偰偟傑偭偰
傕偍偐偟偔偁傝傑偣傫丅
丂憡柕弬偟偨嘆偲嘇傪偳偆偟偰傕棟榑偺婎慴偵偍偒偨偄偨傔偵丄傾僀儞僔儏僞僀儞偼柕弬偟偨尨棟摨巑偺忋偱丄偦偺柕弬
丂憡柕弬偟偨嘆偲嘇傪偳偆偟偰傕棟榑偺婎慴偵偍偒偨偄偨傔偵丄傾僀儞僔儏僞僀儞偼柕弬偟偨尨棟摨巑偺忋偱丄偦偺柕弬
偺榑棟傪梡偄偰帪娫偲偄偆傕偺傪嵞掕媊偟偨偺偱偡丅
帪娫傪揙掙揑偵偹偠嬋偘傞傞偙偲偱丄側傫偲偐偮偠偮傑傪崌傢偣丄偱偒偁偑偭偨偺偑憡懳榑偱偡丅尨棟偲偄偆搚戜偱柍棟
傪偟偰偄傞偺偱偡偐傜丄偳偙偐偵偦偺偟傢婑偣偑偔傞偙偲偼摉慠偺偙偲偩偭偨偺偱偡丅
丂偳偺傛偆偵捯咫傪崌傢偣偨偐偵偮偄偰偼丄壓婰傪嶲徠偔偩偝偄丅
丂偳偺傛偆偵捯咫傪崌傢偣偨偐偵偮偄偰偼丄壓婰傪嶲徠偔偩偝偄丅
丂儃乕傾傗儅僀働儖僜儞側偳偼憡懳惈棟榑偵戝斀懳偩偭偨傛偆偱偡偑丄乽戝揤嵥尰傞両僯儏乕僩儞埲棃偺戝妚柦両乿偲
偄偆丄儅僗僐儈傪娷傔偰偺悽娫偺戝崌彞偑偦傟傜傪墴偟愗偭偰偟傑偭偨偺偱偟傚偆丅巹偑憡懳榑傪傛偔乽偮偠偮傑崌傢偣
偺棟榑乿偲屇傇偺偼埲忋偺傛偆側棟桼偐傜偱偡丅
丂傾僀儞僔儏僞僀儞偼楌巎揑榑暥乽摦偄偰偄傞暔懱偺揹婥椡妛乿偺拞偱丄乽岝懍搙晄曄偺尨棟乿偲乽摿庩憡懳惈尨棟乿
偑柕弬偟偰偄側偄偙偲偺徹柧傪梌偊偰偄傞偺偱偡偑丄偦偺徹柧偑慡偔偺婾傝偱偁傞偙偲傪丄
偱帵偟傑偟偨丅
丂丂偦傟偼嬃偔傋偒媆嵩偺徹柧偲側偭偰偄傑偡丅
丂埲忋偺媍榑偐傜丄摿庩憡懳惈尨棟偲岝懍搙晄曄偺尨棟偼柕弬偟偨傕偺偱偁傞偙偲偑敾柧偟傑偟偨丅
丂暔棟偺嫵壢彂偱偼傛偔乽憡懳榑偺棟榑宍幃偺娙寜偝丄旤偟偝乿偲偄偆偙偲偑嫮挷偝傟傑偡丅
偨偟偐偵丄暔棟妛偵偍偄偰偦傟傕堦偮偺廳梫側梫慺偱偼偁傝傑偡偑丄偟偐偟偄偔傜娙寜偱偁傠偆偲婎慴偵偍偄偨擇偮
偺尨棟偑柕弬偟偰偄傞偺偱偡偐傜丄偦偺忋偵峔抸偝傟偨棟榑偑惓偟偄傕偺偲側傞偙偲偼愨懳偵側偄丄偲偄偆偙偲傪擣幆
偡傞偙偲偑戝愗偱偡丅
丂憡懳榑偺抋惗偑僯儏乕僩儞埲棃偺戝妚柦側偳偲偄傢傟傞偺偼丄乽帪娫丒嬻娫乿偺奣擮傪崻掙偐傜曄偊偰偟傑偭偨偐傜
偱偡偑丄傾僀儞僔儏僞僀儞偺帪娫偵懳偡傞峫嶡偑娫堘偭偰偄偨偺偼丄懠偺條乆側売強偱帵偟偨偲偍傝偱偡丅偠偮偼丄帪娫
偼丄塅拡慡懱偵嫟捠偵棳傟偰偄傞偲栺懇偡傞丄偲偄偆惈幙偺傕偺偩偭偨偺偱偡丅
丂暔棟妛幰偼偄偮婥偯偔偺偱偟傚偆偐丒丒丒
丂暔棟妛幰偼偄偮婥偯偔偺偱偟傚偆偐丒丒丒
丂憡懳榑偱丄巹偑偄偮傕巚偭偰偄傞偙偲偑偁傝傑偡丅偦傟偼乭岝懍搙晄曄偺尨棟乭偵娭偟偰偺偙偲偱偡丅
摿庩憡懳榑偺偙偲偵側傞偲丄乽岝懍搙晄曄偺尨棟偑偙偆偩丄岝懍搙晄曄偺尨棟偼偁偁偩乿偲偄傠偄傠側恖偑庡挘偡傞
偺偱偡偑丄偦傫側偙偲傪尵偭偰傞偐傜丄妀怱晹暘偑偄偮傕晄妋偐側忬懺偵側偭偰偄傞婥偑偟傑偡丅
丂傒側岝懍搙晄曄偺尨棟偲偄偆尨棟傪偄傑傂偲偮偁偄傑偄偵偟偐偮偐傔偰偄側偄偺偱側偄偱偟傚偆偐丅
丂摿庩憡懳惈棟榑偼岝懍搙晄曄偺尨棟偩偗偐傜峔惉偝傟偰偄傞偺偱偼偁傝傑偣傫丅
乽岝懍搙晄曄偺尨棟乿偲偲傕偵丄傕偆堦偮偺拰偱偁傞乽摿庩憡懳惈尨棟乿傪崌傢偣偰峔惉偝傟偰偄傑偡丅
偡側傢偪丄摿庩憡懳榑偼丄
丂嘆岝懍搙晄曄偺尨棟
丂嘇摿庩憡懳惈尨棟
偲偄偆擇偮傪巜摫尨棟偲偟偰嶌傜傟偰偄傞偺偱偡丅
丂傾僀儞僔儏僞僀儞偺岆傝傪偼偭偒傝偲擣幆偡傞偵偼丄僘僶儕嘇摿庩憡懳惈尨棟偵偙偦拲栚偟側偗傟偽側傜偄丅
丂岝懍搙晄曄偺尨棟偽偐傝尒偰偄偰偼僟儊偱偡乮杮幙偑傏傗偗偰偟傑偆乯丅
丂忋偺亙憡懳榑偺尨棟偵傂偦傓棟夝晄壜擻側榑棟揥奐傪柧傜偐偵偡傞亜偱傕愢柧偟傑偟偨偑戝帠側揰偱偡偺偱丄偙
傟傑偱偺婰弎傪傑偲傔傞宍偱嵞搙愢柧偟傑偡丅
丂憡懳榑偺嫵壢彂偵傛偔弌偰偔傞嘆丄嘇丄嘊傪傕偆堦搙彂偒傑偡丅
岝懍搙晄曄偺尨棟嘆乽恀嬻拞偺岝偺懍偝偼岝尮偺塣摦忬懺偵傛傜偢堦掕偱偁傞乿
摿庩憡懳惈尨棟嘇乽暔棟朄懃偼丄偡傋偰偺姷惈宯偵懳偟偰摨偠宍偱偁傜傢偝傟傞乿
丂嘆偼嘇傪峫椂偵擖傟傞偲丄偮偓偺傛偆偵傕昞尰偝傟傑偡丅
摿庩憡懳惈尨棟嘇乽暔棟朄懃偼丄偡傋偰偺姷惈宯偵懳偟偰摨偠宍偱偁傜傢偝傟傞乿
丂嘆偼嘇傪峫椂偵擖傟傞偲丄偮偓偺傛偆偵傕昞尰偝傟傑偡丅
岝懍搙晄曄偺尨棟偺暿昞尰嘊乽偄偐側傞姷惈宯乮娤應幰乯偐傜尒偰傕岝偺懍偝偼堦掕抣們偱偁傞乿
丂偼偭偒傝尵偄傑偡丅
丂嘆偼惓偟偄偑丄嘇偲嘊偑娫堘偭偰偄傞偺偱偡丅
丂忋偺嘆偼丄愄偐傜崱擔傑偱姰帏偵惓偟偄丅偟偐偟丄嘇偑娫堘偭偰偄傞偺偼丄師偱傕巜揈偟偨捠傝懡偔偺幚椺偱柧傜偐
偱偡丅
丂嘇偼姰慡偵岆偭偨尨棟偱偡丅傛偭偰丄嘆偵嘇傪梈崌偝偣偨嘊偑岆傝偲側傞偺偼摉慠偱偁傝傑偡丅
嘇偺傛偆側尨棟傪偄偮傑偱傕愨懳揑尨棟偲偟偰怣曭偟偰偄傞偐傜丄尰戙暔棟偼偳偙傑偱傕偍偐偟側偙偲偵側偭偰偄偔偺
偱偡丅
丂摿庩憡懳惈尨棟偺傛偆側娫堘偭偨尨棟側偳丄憗媫偵幪偰嫀傜側偗傟偽側傝傑偣傫丅妛幰偼偼傗偔婥晅偐側偗傟偽
側傜側偄丅
丂偦偟偰丄偦偺偙偲偵婥晅偄偨偲偒丄幪偰嫀傞桬婥傪傕偭偨偲偒丄備偑傫偩尰戙暔棟偼傑偲傕側忬懺傊偲婣傞偙偲偑偱偒
傑偡丅
