時空と運動と虚数

・運動とは時空の伸び縮みである。

・伸び縮みした時空は虚数方向に曲がる。

・電磁気の関係の式では虚数を用いる。
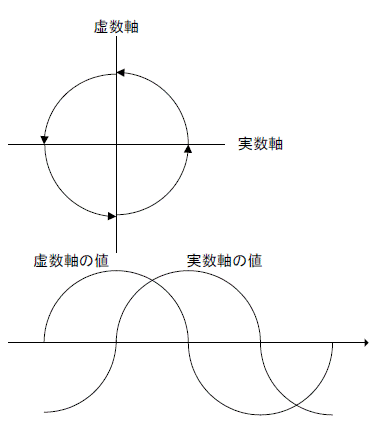
　　　交流においては、電流と電圧の波の位相が９０°ずれる。
　　　これを電流を実数軸と電圧を虚数軸に配置し、
　　　複素数平面を回転する波で表現することがある。
　　　cos(ωt) + i sin(ωt)

　　　

　　　電気と磁気の関係においても同様で、位相が９０°ずれる。
　　　磁力があることによって電力が発生するのではなく、
　　　磁力の変化によって電力が発生する。
　　　（下記の「マクスウェル方程式」を参照）
　　　数学的には、磁力の微分が電力に比例する。
　　　cos の微分はsinなので、結果、位相が９０°ずれることになる。

　　　なぜ、２つの位相がずれた波の片方を虚数にするかというと、
　　　cos(ωt) + i sin(ωt)の式はeiωtと書き換えることができ、
　　　式の表記を簡素化できるからである。

・量子力学の関係の式でも虚数を用いる。
　　　量子の波の式　ψ = cos(kx-ωt) + i sin(kx-ωt)
　　　　　複素数平面を回転する波である
　　　シュレディンガー方程式　ｉħ(∂ψ/∂ｔ) = -(ħ2/2m)(∂2ψ/∂x2) + V(x)ψ

・磁気は電子の運動による時空の縮みで生じる。
　　　「磁力の正体」のページを参照

・重力は電子とクオークの運動による時空の縮みで生じる。
　　　「なぜ質量があると時空が曲がるのか」のページを参照

【参考】

マクスウェル方程式

    次の４つの方程式からなる

    1) rot E = -∂B/∂t
           E:電場 B:磁束密度
           電磁誘導の法則
           磁力の変化によって電流が発生する。

    2) rot H = i + ∂D/∂t
           H:磁場 D:電束密度 i:電流
           電流のつくる磁場に関するアンペールの法則を
           変位電流∂D/∂tを加えて一般化したもの。
           電流によって磁力が発生する。
           電流の流れる方向に対してネジの回転のように磁力が発生する。

    3) div D = ρ
           ρ:電荷密度
           電荷のある物から、外側に電気力線が出ていくことを示す。

    4) div B = 0
           磁力線が閉曲線であることを示す。
           N極から出てS極に入るので、結果、外に出ていかない。

    rot （▽×）
        ベクトル場の回転
        回転軸方向に右回りであることを示す
        負の値の時は左回り

    div （▽・）
        ベクトル場の発散
        ある点から外側に流出ていくことを示す
        負の値の時は流入