円筒形コイル周辺の磁場の絵(その2) 3 薄い円板コイル、4厚みのある円筒コイル
3 薄い円板コイルによる磁場
半径方向の単位幅あたりid (A/m)の電流密度で電流が流れている薄い円板コイルにより作られる磁場について考えてみよう。(^^
円板コイルの外径をao内径を0とする
計算法
3a 半径方向に積分し周方向に数値積分する方法
r、zの位置に作られる磁場のベクトルポテンシャルA_のθ方向成分A_θは角度θ、半径eの位置にある電流素片によって作られる
微少なθ方向成分を加算したものであるから
A_θ=(μid /(2π))∫π_0 dθcosθ (∫ao_0 de e/√(z^2+e^2+r^2-2e r cosθ))
=(μid /(2π))∫π_0 dθcosθ(∫ao_0 de e /√(R^2+e^2-2e r cosθ)) (1)
(√(z^2+r^2) = Rと 略記) eに関する積分部分Ieは
Ie=∫ao_0 de e/√(R^2+e^2-2e r cosθ)
公式∫de e/√(e^2+βe+γ)= √(e^2+βe+γ)-(β/2) ln|2e+β+2√(e^2+βe+γ)|を使って(ここではβ=-2r cosθ; γ= R^2 )
Ie = [√(R^2+e^2-2e r cosθ)+r cosθln|2e-2r cosθ+2√(R^2+e^2-2e r cosθ)|] ao_0
=√(R^2+ao^2-2ao r cosθ)+ r cosθln|2ao-2r cosθ+2√(R^2+ao^2-2ao r cosθ)|-(R+ (r cosθl n|-2r cosθ+2R|))
θに関する積分の部分Iθは
Iθ=∫π_0 dθ (cosθ√(R^2+ao^2-2ao r cosθ)+ r cos^2θln|2ao-2r cosθ+2√(R^2+ao^2-2ao r cosθ)|
- R cosθ-(r cos^2θln|-2r cosθ+2R|))
残念ながらcos^2θの項があるためこの積分は標準的な楕円積分では表わせないので
この式のままシンプソンの1/3公式を使って数値積分を行うのがベスト。
(θ方向に32等分程度分割すれば十分な精度が出る)
ここで若干コメントしますと太さ一定の電線を円板状にすきまなく巻いてコイルを作ると巾あたりの電流密度が半径にかかわらず一定な
等電流密度分布のコイルが出来るが芯のところでは巻くことが物理的に不可能である。すなわち等電流密度分布の円板コイルというものは
中心部で物理的に破綻している物で本当は考えてはいけない物なのですが破綻している領域の体積が0なので答えは出てくる。
なお電線を巻くのを途中でやめて中空のドーナツ板の様なコイルを作れば破綻はない。
それに対して外周で目一杯密に巻き内部の半径eの所では電線の密度がe/aoに比例するようにすきまをとって疎に電線を巻いていけば
電流密度が半径に比例する剛体渦形電流密度分布のコイルが作れる。
剛体渦形電流密度分布だとcos^2θやsin^2θなどの偶数次の項は現れず標準的な楕円積分で表す事が出来る。
シンプソンの1/3公式というのは被積分関数(曲線)を区分的に二次曲線で近似して積分値(面積)を求める方法で具体的には次のようになります。
一般的な場合、独立変数xの領域を偶数個、例えば2m=32ヶに等分割し、下限点をx_0、上限点をx_32、
最初の分割点をx_1、2番目の分割点をx_2というように順番に番号をつけると
まず区間x_0〜x_2の間で区間内の被積分曲線f(x)の区分点での値をf_0= f( x_0),f_1= f(x_1) ,f_2= f(x_2)とし
この区間で被積分曲線を三つの点(x_0,f_0)、(x_1,f_1)、(x_2,f_2 )を通る二次曲線yで近似すると区間巾Δ= (x_32-x_0)/(2m)として
y=((f_0-f_2)/2-f_1)(x-x_1)^2/Δ^2であるからこの区間での積分の近似値I_1は
I_1=∫(x_2)_(x_0) dx ((f_0-f_2)/2-f_1)(x-x_1)^2/Δ^2=((f_0-f_2)/2-f_1)((x_2-x_1)^3-(x_0-x_1)^3)/(3Δ^2)=2((f_0-f_2)/2-f_1)Δ^3/(3Δ^2)
=(1/3)Δ((f_0-f_2)-2f_1) (∫(x_2)_(x_0)はx_0からx_2までの定積分を表しています)
x_2〜x_4, x_4〜x_6,…でも同様な事を繰り返して足し合わせると区間0〜32での近似値Iは
I≒Δ((1/3)(f_0+f_32)+4(f_1+f_3+…)/3+2(f_2+ f_4+…)/3)
実際にIθを数値積分すると独立変数はθで下限でθ_0=0, 上限でθ_32=πであるから領域巾はπ、区間巾Δは Δ=π/32
被積分関数fの分割点での値は
f(θ)= cosθ√(R^2+ao^2-2ao r cosθ)+ r cos^2θln|2ao-2r cosθ+2√(R^2+ao^2-2ao r cosθ)|- R cosθ-(r cos^2θln|-2r cosθ+2R|))
にθ_0=0,θ_1=π/32,…,θ_32=π を代入した値を使用し
Iθ≒Δ((1/3)(f_0+f_32)+4(f_1+f_3+…+f_31)/3+2(f_2+ f_4+…+f_30)/3)
A_θ=(μid /(2π)) Iθ
ψ=(1/μ) r A_θ
となる。
3b 周方向に積分し半径方向に数値積分する方法
(1)式を先にθで積分する形に書き換えると
A_θ=(μid /(2π)) (∫ao_0 de e(∫π_0 dθcosθ/√(z^2+e^2+r^2-2e r cosθ))
その1の 単線輪コイルの磁場の計算より
Iθs= ∫π_0 dθcosθ/√(z^2+e^2+r^2-2e r cosθ)= (2/α)((2/k^2-1) Z1(k)-(2/k^2) Z2(k)))
(√(z^2+(e+r)^2) =α; 4e r/α^2 = k^2 と略記)
であるから
A_θ=(μid /(2π))(∫ao_0 de e Iθs) =(μid /(2π)) Ie
eに関する積分部分Ieを実際に数値積分すると独立変数はeで下限でe_0=0, 上限でe_32=aoであるから領域巾はao、区間巾Δは Δ=ao/32
被積分関数fの分割点での値は
f(e)= e (2/α)((2/k^2-1) Z1(k)-(2/k^2) Z2(k)))
にe_0=0,e_1=ao/32,…,e_32=aoを代入した値を使用し
Ie≒Δ((1/3)(f_0+f_32)+4(f_1+f_3+…+f_31)/3+2(f_2+ f_4+…+f_30)/3)
A_θ=(μid /(2π)) Ie
円柱座標での流れ関数ψは
ψ=(1/μ) r A_θ
となる。
なおaiをコイルの内半径として積分∫ao_0 de e Iθsを積分∫ao_ ai de e Iθs で行えば中空円板コイルの磁場の絵が得られる。
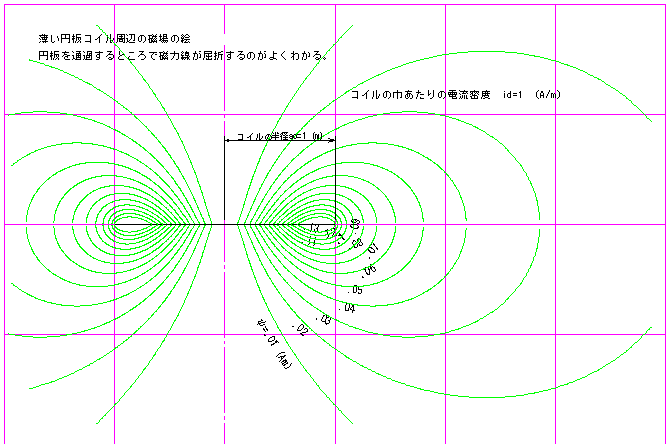
薄い円板コイル周辺の磁場の絵
円板を通過するところで磁力線が屈折するのがよくわかる。(^^
4厚みのある円筒コイル周辺の磁場
単位断面積あたりid (A/m^2)の電流密度で電流が流れている厚い円筒コイルにより作られる磁場について考えてみよう。(^^
円筒コイルの外径をao内径を0長さを2Hとする
r、zの位置に作られる磁場のベクトルポテンシャルA_のθ方向成分A_θは高さh、半径e、角度θの位置にある
電流素片によって作られる微少な成分を加算したものであるから
A_θ=( id /(2π)) ∫ao_0 de e∫π_0 dθcosθ∫H_-H dh /√((h-z)^2+e^2+r^2-2e r cosθ)
計算法
積分 IθS =∫π_0 cosθdθ∫H_-H dh /√((h-z)^2+e^2+r^2-2e r cosθ)はその1の薄い円筒コイルの磁場によれば
IθS =2((H-z)/(αm)((2/km^2+(a-r)^2/(2a r)) Z1(km)-(2/km^2) Z2(km)-((a-r)^2/(2a r)) Z3(kc,km))
+((H+z)/(αp)((2/kp^2+(a-r)^2/(2a r)) Z1(kp)-(2/kp^2) Z2(kp)-((a-r)^2/(2a r)) Z3(kc,kp))
(kc=-4a r/(a+r)^2; αm=√((H-z)^2+(a+r)^2); km^2=4a r/αm^2; αp=√((H+z)^2+(a+r)^2); kp^2=4a r/αp^2 と略記 )
であるから
A_θ=( id /(2π)) ∫ao_0 de e IθS=( id /(2π)) Ie
eに関する積分部分Ieを実際に数値積分すると独立変数はeで下限でe_0=0, 上限でe_32=aoであるから領域巾はao、区間巾Δは Δ=ao/32
被積分関数fの分割点での値は
f(e)=2e ((H-z)/(αm)((2/km^2+(a-r)^2/(2a r)) Z1(km)-(2/km^2) Z2(km)-((a-r)^2/(2a r)) Z3(kc,km))
+((H+z)/(αp)((2/kp^2+(a-r)^2/(2a r)) Z1(kp)-(2/kp^2) Z2(kp)-((a-r)^2/(2a r)) Z3(kc,kp))
にe_0=0,e_1=ao/32,…,e_32=aoを代入した値を使用し
Ie≒Δ((1/3)(f_0+f_32)+4(f_1+f_3+…+f_31)/3+2(f_2+ f_4+…+f_30)/3)
A_θ=(μid /(2π)) Ie
ψ=(1/μ) r A_θ
となる。
なおaiをコイルの内半径として積分∫ao_0 de e Iθsを積分∫ao_ ai de e Iθs で行えば中空円筒コイルの磁場の絵が得られる。
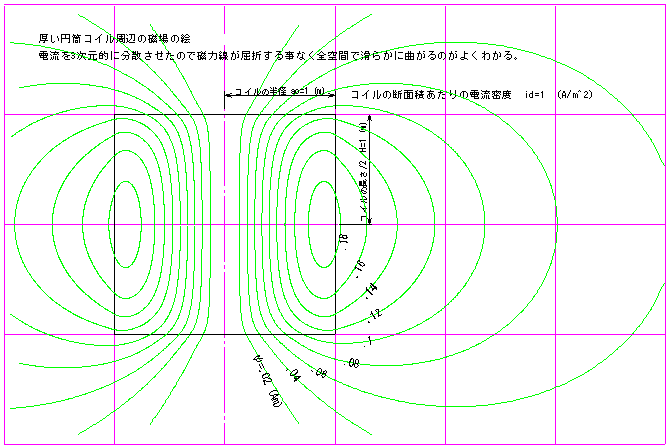
厚い円筒コイル周辺の磁場の絵
電流を三次元的に分散させたので磁力線が屈折する事なく全空間で滑らかに曲がるのがよくわかる。(^^
円筒形コイル周辺の磁場の絵(その1) 1単線輪コイル、2薄い一重円筒コイルへ
円筒形コイル周辺の磁場の絵(その3) (球面形コイル周辺の磁場の絵) 5薄い球面コイル、6回転帯電球面へ