円筒形コイル周辺の磁場の絵(その1) 1単線輪コイル、2薄い一重円筒コイル
何も目新しいものではありませんが本等でなかなか見る事が出来ない円筒形コイル周辺の磁場の絵をここに記載します。
山水画の一種としてお楽しみ下さい。
1単線輪コイル周辺の磁場
単線輪コイルの電流素片と磁場測定点の磁場のベクトルポテンシャルと磁場の成分の関係の図
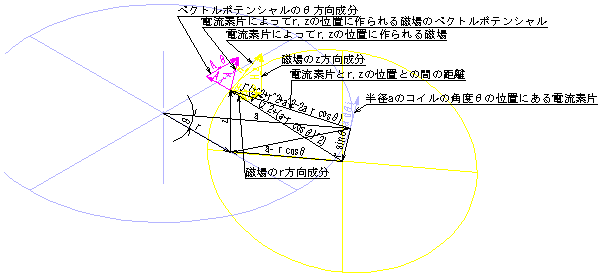
単線輪コイルの磁場のベクトルポテンシャルの計算をしてみよう
円柱座標を採用しコイルはz=0の面内に存在し半径a (m)としi(A)の電流を流すとしよう
r、zの位置に作られる磁場のベクトルポテンシャルA_のθ方向成分A_θはθの位置にある電流素片i dθaによって作られる微少成分を加算したものであるから
A_θ=μ(i/2π)∫π_0 dθ a cosθ/√(z^2+a^2+r^2-2a r cosθ) ( ∫π_0は0からπまでの定積分を表しています)
(μは透磁率です)
θ=π-2φと変数変換すると (dθ=-2 dφ; cosθ=2sin^2φ-1) ( sin^2φは(sinφ)^2の事ですよね)
A_θ=μ(i a /(2π))∫π/2_0 2dφ(2sin^2φ-1)/√(z^2+a^2+r^2-2a r(2sin^2φ-1))=μ(i a /π)∫π/2_0 dφ (2 sin^2φ-1)/√(z^2+(a+r)^2-4a r sin^2φ)
=μ(i a /(πα)∫π/2_0 dφ(2sin^2φ-1)/√(1-k^2 sin^2φ)
=μ(i a /(πα)((2/k^2)(Z1(k)-Z2(k))-Z1(k))= μ(i a /(πα))((2/k^2-1) Z1(k)-(2/k^2) Z2(k))
(Z1(k)は第1種完全楕円積分、Z2(k)は 第2種完全楕円積分です)
(√(z^2+(a+r)^2) =α; 4a r/α^2 = k^2 (1) と略記)
このベクトルポテンシャルA_θにrの値を掛けμで割ったψ=(1/μ) r A_θが磁力線を表す流れ関数となる。
A_θから磁場を計算する
rot(A_)_r =(∂A_z/∂θ)/r-∂A_θ/∂z
rot(A_)_θ =∂A_r/∂z-∂A_z/∂r
rot(A_)_z =∂A_θ/∂r+A_θ/r –(∂A_r/∂θ)/r
より
磁場のz方向成分H_zは
H_z= (1/μ)rot(A_)_z =(1/μ)(∂A_θ/∂r +A_θ/r ) = (i a /2π) (∂/∂r)∫π_0 dθ cosθ/√(z^2+a^2+r^2-2a r cosθ)
-(i a /(πα)((2/k^2-1) Z1(k)-(2/k^2) Z2(k))/r
偏微分の演算(∂/∂z ) は定積分の演算∫π_0 dθと可換なので先に偏微分を行う
Il =(∂/∂r)∫π_0 dθcosθ/√(z^2+a^2+r^2-2a r cosθ)=∫π_0 dθ(∂/∂r)(cosθ/√(z^2+a^2+r^2-2a r cosθ))
=∫π_0 dθcosθ(2r-2a cosθ)/(2 (z^2+a^2+r^2-2a r cosθ)^(3/2))= ∫π_0 dθcosθ(r-a cosθ)/(z^2+a^2+r^2-2a r cosθ)^(3/2)
θ=π-2φと変換; dθ=-2 dφ; cosθ=2sin^2φ-1
Il = -2∫π/2_0 dφ(2sin^2φ-1)(r-a(2sin^2φ-1))/(z^2+a^2+r^2-2a r(2sin^2φ-1))^(3/2)
=-2∫π/2_0 dφ(2sin^2φ-1)(-2a sin^2φ+r+a)/( z^2+(a+r)^2-4a rsin^2φ)^(3/2)
=-2∫π/2_0 dφ (-4a sin^4φ+2(r+2a) sin^2φ-(r+a))/( z^2+(a+r)^2-4a rsin^2φ)^(3/2)
=(-2/α^3)(-4a(-(2/k^4) Z1(k)+((1+1/(1-k^2))/k^4) Z2(k))+2(r+2a)(-(1/k^2) Z1(k)+(1/(k^2 (1-k^2)) Z2(k))-((r+a)/(1-k^2)) Z2(k))
=(-2/α^3)((8a/k^4)-2(r+2a)/k^2) Z1(k)+((1+1/(1-k^2))/k^4)+(1/(k^2 (1-k^2))-(r+a)/(1-k^2)) Z2(k)
H_z= (i a /2π) Il-(i a /(πα)((2/k^2-1) Z1(k)-(2/k^2) Z2(k))/r
=(i a /2π)(-2/(πα^3)))((8a/k^4)-2(r+2a)/k^2) Z1(k)+((1+1/(1-k^2))/k^4)+(1/(k^2 (1-k^2))-(r+a)/(1-k^2)) Z2(k)
-(i a /(πα)((2/k^2-1) Z1(k)-(2/k^2) Z2(k))/r
=(i a /πα^3))(((8a/k^4)-2(r+2a)/k^2) Z1(k)+((1+1/(1-k^2))/k^4)+(1/(k^2 (1-k^2))-(r+a)/(1-k^2)) Z2(k)-(α^2/r)((2/k^2-1) Z1(k)-(2/k^2) Z2(k)))
(1)から α^2/r = 4a/k^2であるので
H_z=(i a /πα^3))(((8a/k^4)-2(r+2a)/k^2-(4a/k^2)(2/k^2-1)) Z1(k)+((1+1/(1-k^2))/k^4)+(1/(k^2 (1-k^2))-(r+a)/(1-k^2)+(4a/k^2)(2/k^2)) Z2(k)
=- (i a /(πα^3)))((2r/k^2) Z1(k)+((a+r)k^2-2r)/(k^2 (1-k^2))) Z2(k))
磁場のr 方向成分H_rは
H_r= (1/μ)rot(A_)_r =-(1/μ)∂A_θ/∂z=- (i /2π)(∂/∂z )∫π_0 dθ a cosθ/√(z^2+a^2+r^2-2a r cosθ)
(∂/∂z ) a cosθ/√(z^2+a^2+r^2-2a r cosθ) = a z cosθ/(z^2+a^2+r^2-2a r cosθ)^(3/2)であるから
H_r= - (i /2π) ∫π_0 dθ a z cosθ/(z^2+a^2+r^2-2a r cosθ)^(3/2)
θ=π-2φと変換; dθ=-2 dφ; cosθ=2sin^2φ-1
H_r =- (i /2π)∫π/2_0 -2dφa z( 2sin^2φ-1))/(z^2+a^2+r^2-2a r(2sin^2φ-1))^(3/2)
=- (i a z/π)∫π/2_0 dφ ( 2sin^2φ-1))/( z^2+(a+r)^2-4a rsin^2φ)^(3/2)
=- (i a z/(πα^3)))∫π/2_0 dφ(-1+2sin^2φ)/(1-k^2 sin^2φ)^(3/2)
=- (i a z/(πα^3)))((-1/(1-k^2)) Z2(k)+(2/(k^2 (1-k^2)))(-(1-k^2) Z1(k)+Z2(k)))
=- (i a z/(πα^3)))((2/k^2) Z1(k)+((-k^2+2)/(k^2 (1-k^2))) Z2(k))
なおこのようにベクトルポテンシャルを微分して積分を行う計算はビオサバールの法則で直接磁場の計算を行うやり方と同じになっています。
単線輪コイル周辺の磁場の絵
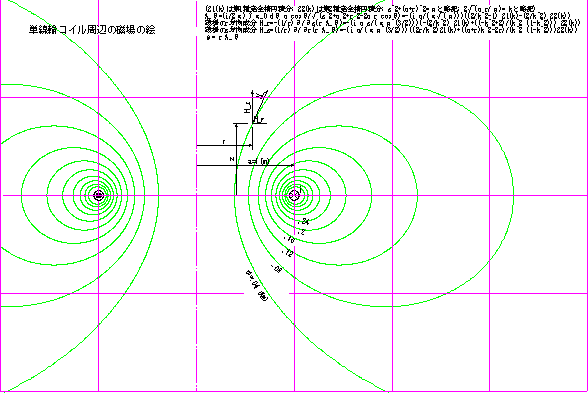
2薄い一重円筒コイル周辺の磁場
単位長さあたりj (A/m)の電流密度で電流が流れている薄い一重円筒コイルにより作られる磁場について考えてみよう。(^^
コイルの半径をa長さを2Hとする。
半径r、高さzの位置に作られる磁場のベクトルポテンシャルA_のθ方向成分A_θは角度θ、高さhの位置にある電流素片によって作られる
微少なθ方向成分を加算したものであるから
A_θ=μ(a j /2π)∫π_0 cosθdθ∫H_-H dh/√((z-h)^2+a^2+r^2-2a r cosθ)
hに関する積分の部分Ihは
Ih=∫H_-H dh/√((h-z)^2+a^2+r^2-2a r cosθ) =∫H_-H dh/√(h^2-2z h+z^2+a^2+r^2-2a r cosθ)
公式∫dx /√(x^2+βx+γ)=ln|2x+β+2√(x^2+βx+γ)|を使って (ここではβ=-2z; γ= z^2+a^2+r^2-2a r cosθ)
(||は括弧の中の数値の絶対値をとる機能つきの括弧という意味でabs()の事で対数関数lnの中を負にしないためのものですが
複素数で考えればlnの中は負でもよいし微分して中を外に出せば消えるものであってあまり深く考える必要はないです。)
Ih=[ln|2h-2z+2√(h^2-2z h+ z^2+a^2+r^2-2a r cosθ)|]H_-H
= ln|(H−z)+√((H−z)^2+a^2+r^2−2a r cosθ)|-ln|-(H+z)+√((H+z)^2+a^2+r^2−2a r cosθ)|
θに関する積分の部分Iθは
Iθ=∫π_0 cosθdθIh
部分積分により
Iθ= [ sinθ(ln|(H−z)+√((H−z)^2+a^2+r^2−2a r cosθ)|-ln|-(H+z)+√((H+z)^2+a^2+r^2−2a r cosθ)|)] π_0
-∫π_0 dθsinθa r sinθ(1/√((H-z)^2+a^2+r^2-2a r cosθ)/((H-z)+√((H-z)^2+a^2+r^2-2a r cosθ))
-1/√((H+z)^2+a^2+r^2-2a r cosθ)/(-(H+z)+√((H+z)^2+a^2+r^2-2a r cosθ)))
Iθの前の部分の独立変数の下限値、上限値を代入するだけの項
IθD=[ sinθ(ln|(H−z)+√((H−z)^2+a^2+r^2−2a r cosθ)|-ln|-(H+z)+√((H+z)^2+a^2+r^2−2a r cosθ)|)] π_0
はsinπ=0 ; sin0=0であることから0
したがってIθの後ろの部分の積分を行う項IθSだけを計算すれば良い。
IθSの前の項の分子、分母に(H-z)-√((H-z)^2+a^2+r^2-2a r cosθ)を掛け、
後ろの項の分子、分母に-(H+z)-√((H+z)^2+a^2+r^2-2a r cosθ)を掛けて分母を有理化すると
IθS=-a r∫π_0 dθsin^2θ(((H-z)/√((H-z)^2+a^2+r^2-2a r cosθ)-1)/((H-z)^2-((H-z)^2+a^2+r^2-2a r cosθ))
-(-(H+z)/√((H+z)^2+a^2+r^2-2a r cosθ)-1)/((H+z)^2-((H+z)^2+a^2+r^2-2a r cosθ)))
=a r∫π_0 dθ((1-cos^2θ)/(a^2+r^2-2a r cosθ))((H-z)/√((H-z)^2+a^2+r^2-2a r cosθ)+(H+z)/√((H+z)^2+a^2+r^2-2a r cosθ))
となり有理関数の部分Y=(1-cos^2θ)/(a^2+r^2-2a r cosθ)は
Y=cosθ/(2a r)+(a^2+r^2)/(2a r)^2-((a+r)^2(a-r)^2/(2a r)^2)/(a^2+r^2-2a r cosθ)
と部分分数に展開出来るから
IθS=∫π_0 dθ(cosθ/2+(a^2+r^2)/(4a r)-((a+r)^2 (a-r)^2/(4a r))/(a^2+r^2-2a r cosθ))
((H-z)/√((H-z)^2+a^2+r^2-2a r cosθ)+(H+z)/√((H+z)^2+a^2+r^2-2a r cosθ))
θ=π-2φと変数変換すると (dθ=-2 dφ; cosθ=2sin^2φ-1)
IθS =2∫π/2_0 dφ(2sin^2φ-1)/2+(a^2+r^2)/(4a r)-((a+r)^2 (a-r)^2/(4a r))/(a^2+r^2-2a r(2sin^2φ-1))
((H-z)/√((H-z)^2+a^2+r^2-2a r(2sin^2φ-1))+(H+z)/√((H+z)^2+a^2+r^2-2a r(2sin^2φ-1))
=-∫π/2_0 dφ(2sin^2φ+(a-r)^2/(2a r)-((a+r)^2 (a-r)^2/(2a r))/((a+r)^2-4a r sin^2φ))
((H-z)/√((H-z)^2+(a+r)^2-4a r sin^2φ)+(H+z)/√((H+z)^2+(a+r)^2-4a r sin^2φ)
=-∫π/2_0 dφ(2sin^2φ+(a-r)^2/(2a r)-((a-r)^2/(2a r))/(1+kc sin^2φ))
((H-z)/(αm √(1-km^2 sin^2φ))+(H+z)/(αp √(1-kp^2 sin^2φ)))
(kc=-4a r/(a+r)^2; αm=√((H-z)^2+(a+r)^2); km^2=4a r/αm^2; αp=√((H+z)^2+(a+r)^2); kp^2=4a r/αp^2 と略記 )
公式 ∫π/2_0 dφ sin^2φ/√(1-k^2 sin^2φ)= (1/k^2)(Z1(k)-Z2(k))を使い
IθS=- ((H-z)/αm)(( 2/km^2)(Z1(km)-Z2(km))+((a-r)^2/(2a r)) Z1(km)-((a-r)^2/(2a r)) Z3(kc,km))
+((H+z)/αp)(( 2/kp^2)(Z1(kp)-Z2(kp))+((a-r)^2/(2a r)) Z1(kp)-((a-r)^2/(2a r)) Z3(kc,kp))
=((H-z)/αm)((2/km^2+(a-r)^2/(2a r)) Z1(km)-(2/km^2) Z2(km)-((a-r)^2/(2a r)) Z3(kc,km))
+((H+z)/αp)((2/kp^2+(a-r)^2/(2a r)) Z1(kp)-(2/kp^2) Z2(kp)-((a-r)^2/(2a r)) Z3(kc,kp))
( Z3(kc,k)は第3種完全楕円積分です)
A_θ=μ( a j /2π) IθS
ベクトルポテンシャルのθ方向成分A_θにrの値を掛けμで割った物が磁力線を表す円柱座標での流れ関数ψとなる。(^^
ψ=(1/μ) r A_θ
薄い一重円筒コイル周辺の磁場の絵
薄い円筒コイルを通過する磁力線はコイルの所で屈折する。
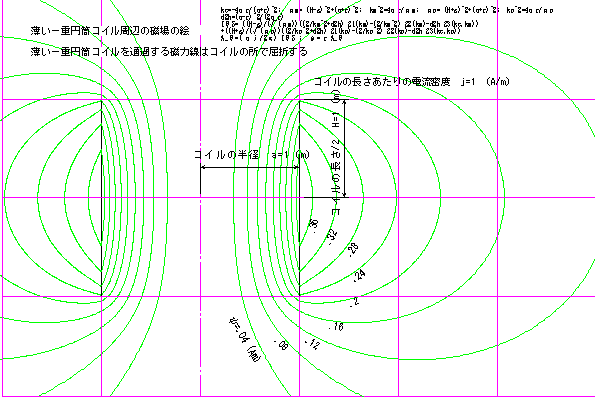
ここでも磁場のz方向成分r方向を計算するとよいのですがさしあたり磁力線の絵を描くには必要ないので時間のある時にやろうと思っています。
円筒形コイル周辺の磁場の絵(その2) 3 薄い円板コイル、4厚みのある円筒コイルへ