墌摏宍僐僀儖廃曈偺帴応偺奊(偦偺3)丂乮媴柺宍僐僀儖廃曈偺帴応偺奊乯
5敄偄媴柺僐僀儖廃曈偺帴応丄丂6夞揮懷揹媴柺廃曈偺帴応
5丂敄偄媴柺僐僀儖廃曈偺帴応
墌廃曽岦偺扨埵暆偁偨傝id (A/m)偺揹棳枾搙偱揹棳偑棳傟偰偄傞敄偄媴柺僐僀儖偵傛傝嶌傜傟傞帴応偵偮偄偰峫偊偰傒傛偆丅(^^
愨墢懱偱抧媴媀偺傛偆側媴柺懱傪嶌傝偦偺忋偵堒搙慄偺曽岦偵懢偝堦掕偺揹慄傪姫偒晅偗偰偄偔偺偱偁傞偑
愒摴偺偁偨傝偱偼墌摏僐僀儖偺傛偆偱偁傞偐傜姫偒傗偡偄偑嬌偵嬤偔側傞偵偮傟偰墌斅僐僀儖偺傛偆偵側傝
姫偄偰傕曵傟傞偺偱愙拝嵻偱揬傝晅偗側偑傜姫偄偰偄偔偟偐側偄丅
偦偟偰墌斅僐僀儖偲摨條偵椉嬌偱暔棟揑偵攋抅偡傞偑攋抅偟偰偄傞椞堟偺懱愊偑0偱偁傞偐傜摎偊偼弌偰偔傞丅
媴柺偺敿宎傪a偲偡傞丅
宱搙偵憡摉偡傞妏搙傪偙偙偱偼墌拰嵗昗傕巊偆偲偄偆帠偱兤偲偟傛偆丅
堒搙偵懳墳偡傞妏搙傪杒嬌懁偐傜應偭偰冊(僇僀)偲偟傛偆丅
r丄z偺埵抲偵嶌傜傟傞帴応偺儀僋僩儖億僥儞僔儍儖A_偺兤曽岦惉暘A_兤偼兤丄冊偺埵抲偵偁傞
揹棳慺曅id a sin冊d冊a d兤偵傛偭偰嶌傜傟傞旝彮側兤曽岦惉暘傪壛嶼偟偨傕偺偱偁傝
應掕揰偲揹棳慺曅偺娫偺嫍棧l偑l=併((z-a cos冊)^2+a^2 sin^2冊+r^2-2a r sin冊cos兤) =併(a^2+z^2+r^2-2a (z cos冊+r sin冊cos兤)偱偁傞偐傜
A_兤=(兪a^2 id /(2兾))佺兾_0 d冊sin冊(佺兾_0 d兤cos兤/併(a^2+z^2+r^2-2a (z cos冊+r sin冊cos兤))丂丂(1)
=(兪a^2 id /(2兾W))佺兾_0 d冊sin冊 (佺兾_0 d兤cos兤/併(1-(kz cos冊+kr sin冊cos兤) (2)
(a^2+z^2+r^2=W^2丟 kz=2a z/W^2丟丂kr=2a r/W^2偲 棯婰)丂
5a媺悢揥奐偵傛傞寁嶼朄
(2)偺暘曣偺崻崋偺拞偺(kz cos冊+kr sin冊cos兤)傪揥奐岞幃偵傛傝堦婥偵暘巕偵忋偘偰媺悢揥奐傪峴偆丅
A_兤=(兪a^2 id /(2兾W))佺兾_0 d兤cos兤(佺兾_0 sin冊d冊(1+(1/2)(kz cos冊+kr sin冊cos兤)+(1/2)(3/4) (kz cos冊+kr sin冊cos兤)^2+乧)
愊暘偼慡晹0偐傜兾傑偱偺掕愊暘側偺偱偦偺揰偼娙扨偱偁傞丅
偟偐偟媴柺偺嬤偔偱偼k偑1偵嬤偄戞1庬懭墌愊暘偺媺悢揥奐偲摨偠尨棟偱廂懇偺懍搙偑嬌傔偰彫偝偔側傝岆嵎偑廤愊偟偰惛搙偑埆偔側傞偐傜
師偺宱搙曽岦(兤曽岦乯偵愊暘偟堒搙曽岦(冊曽岦乯偵悢抣愊暘偡傞曽朄偺専嶼梡偵偟偐側傜側偄丅
5b宱搙曽岦(兤曽岦乯偵愊暘偟堒搙曽岦(冊曽岦乯偵悢抣愊暘偡傞曽朄
(1)幃偱兤偱愊暘偡傞晹暘偼
I兤=佺兾_0 d兤cos兤/併((a^2+z^2+r^2-2a (z cos冊+r sin冊cos兤)) =佺兾_0 d兤cos兤/併((a^2+z^2+r^2-2a (z cos冊+r sin冊cos兤))
兤=兾-2冇偲曄悢曄姺偡傞偲丂(d兤=-2 d冇; cos兤=2sin^2冇-1)
I兤=2佺兾/2_0 d冇(2sin^2冇-1)/併((a^2+z^2+r^2-2a z cos冊+2a r sin冊)-4a r sin冊sin^2冇))
= 2/兛佺兾/2_0 d冇(2sin^2冇-1)/併(1-k^2 sin^2冇)
(併(a^2+r^2+z^2-2a z cos冊+2a r sin冊) =兛; 4 a r sin冊/兛^2 = k^2丂偲棯婰)
=2/兛((2/k^2)(Z1(k)-Z2(k))-Z1(k))=丂 (2/兛)((2/k^2-1) Z1(k)-(2/k^2) Z2(k))
(Z1(k)偼戞1庬姰慡懭墌愊暘丄Z2(k)偼 戞2庬姰慡懭墌愊暘偱偡)
偙傟偐傜
A_兤=(兪id /2兾)佺兾_0 d冊sin冊(2/兛)((2/k^2-1) Z1(k)-(2/k^2) Z2(k))
=(兪id /2兾) I冊
冊偵娭偡傞愊暘晹暘I冊傪幚嵺偵悢抣愊暘偡傞偲撈棫曄悢偼冊偱壓尷偱冊_0=0, 忋尷偱冊_32=兾丂偱偁傞偐傜椞堟嬓偼兾丄嬫娫嬓儮偼丂儮=兾/32
旐愊暘娭悢f偺暘妱揰偱偺抣偼
f(冊)= sin冊(2/兛)((2/k^2-1) Z1(k)-(2/k^2) Z2(k)))
偵冊_0=0丆冊_1=兾/32丆乧丆冊_32=兾傪戙擖偟偨抣傪巊梡偟
I冊佮儮((1/3)(f_0+f_32)+4(f_1+f_3+乧+f_31)/3+2(f_2+ f_4+乧+f_30)/3)
A_兤=(兪id /(2兾)) I冊
墌拰嵗昗偱偺棳傟娭悢冋偼r傪偐偗偰
冋=(1/兪) r A_兤
偲側傞丅(^^
敄偄媴柺僐僀儖廃曈偺帴応偺奊
揹慄偺暻偑嬌偵嬤偯偔偵偮傟偰撪懁偵嬋偑偭偰偄傞偺偱媴柺偺撪晹偱偼帴椡慄傕撪懁傊嬋偑偭偰偄傞(^^
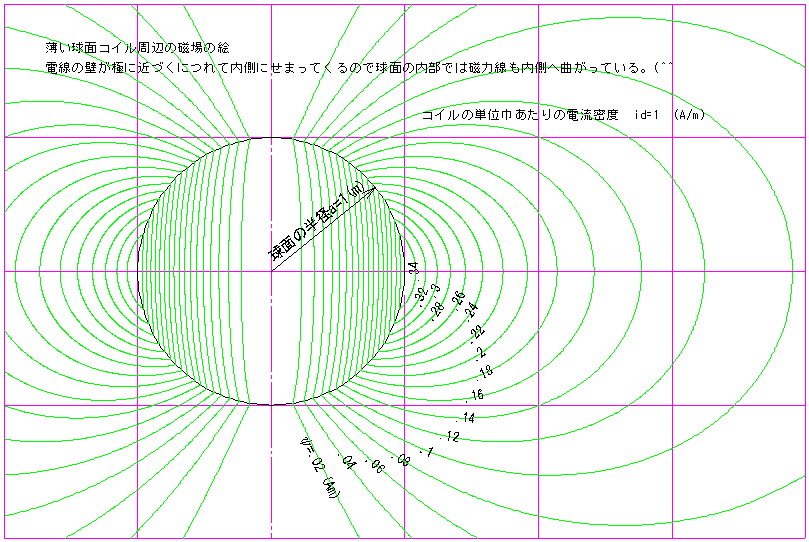
6夞揮懷揹媴柺廃曈偺帴応乮敿宎偵斾椺偡傞揹棳枾搙偺媴柺僐僀儖偵傛傞帴応乯
愒摴晅嬤偱偼揹慄傪栚偄偭傁偄枾偵姫偒幉偵嬤偯偔偵偮傟偰幉偐傜偺嫍棧偵斾椺偡傞枾搙偱傑偽傜偵姫偄偨媴柺僐僀儖偵傛偭偰嶌傜傟傞帴応
偵偮偄偰峫偊偰傒傛偆丅(^^
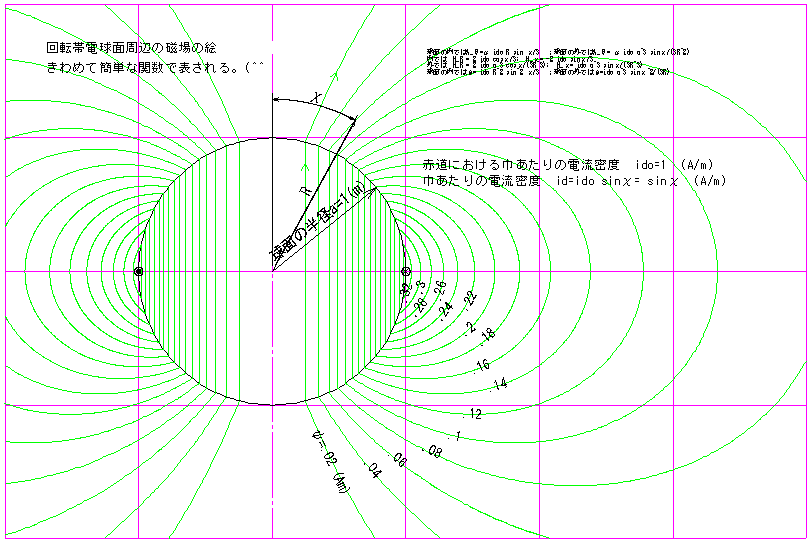
偙傟偼廃曈偐傜愨墢偟偨敄偄嬥懏媴柺偵揹壸傪梌偊偰懷揹偝偣夞揮偝偣偨帪弌棃傞帴応偲摍壙偺帴応偱偁傞丅
媴嵗昗傪巊偄應掕揰偺嵗昗傪應掕揰偐傜媴柺偺拞怱傑偱偺嫍棧傪R丆宱搙偵憡摉偡傞妏搙傪兤丆杒嬌懁偐傜應偭偨堒搙偵憡摉偡傞妏搙傪冊偲偟傛偆丅
媴柺偺敿宎傪a偲偡傞丅愒摴忋偱偺嬓偁偨傝偺揹棳枾搙傪ido偲偟妏搙冊0偺応強偱偺揹棳枾搙i d= ido丂sin冊0偲偟傚偆
r丄z偺埵抲偵嶌傜傟傞帴応偺儀僋僩儖億僥儞僔儍儖A_偺兤曽岦惉暘A_兤偼兤丄冊0偺埵抲偵偁傞
揹棳慺曅ido sin冊0 a sin冊0 d冊0 a d兤偵傛偭偰嶌傜傟傞旝彮側兤曽岦惉暘傪壛嶼偟偨傕偺偱偁傝
應掕揰偲揹棳慺曅偺娫偺嫍棧l偑l=併((z-a cos冊0)^2+a^2 sin^2冊0+r^2-2a r sin冊0 cos兤) =併(a^2+z^2+r^2-2a (z cos冊0+r sin冊0 cos兤)偱偁傞偐傜
A_兤=( ido a^2 /(2兾))佺兾_0 d冊0 sin^2冊(佺兾_0 d兤cos兤/併(a^2+z^2+r^2-2a (z cos冊0+r sin冊0 cos兤))
幚偼偙偺愊暘傪幚峴偟側偔偰傕旝暘曽掱幃揑側峫嶡偐傜摎偊偼傢偐偭偰儀僋僩儖億僥儞僔儍儖A_偺兤曽岦惉暘A_兤偼媴嵗昗偱昞偟偰
媴柺偺撪偱偼A_兤=丂兪 ido R sin 冊/3丂丂丂丂(3)
媴柺偺奜偱偼A_兤=丂兪 ido a^3 sin冊/(3R^2)丂 丂丂(4)
偲側傞丅
側偤偐偲尵偆偲H_=(1/兪) rot(A_)偵傛傝帴応儀僋僩儖H_傪寁嶼偡傞偲
H_R =(1/兪)rot(A_)_R=(1/兪)(佪A_兤/佪冊)/R +cot冊A_兤/R; H_冊=(1/兪)rot(A_)_冊=(1/兪)(–佪A_兤/佪R–A_兤/R)
偱偁傞偐傜
撪偱偼 H_R = 2 ido cos冊/3; H_冊= –2 ido sin冊/3
奜偱偼 H_R = 2 ido a^3 cos冊/(3R^3); H_冊= ido a^3 sin冊/(3R^3)
帴応偵傕偆堦夞rotation傪傎偳偙偟帴応偺塓搙傪媮傔傞偲rot(H _)_兤=(佪H_冊/佪R)+ H_冊/R -(佪H_R/佪冊)/R丂偱偁傞偐傜
撪偱偼丂rot(H_)_R= 0;丂rot(H_)_兤= –2 ido sin冊/3/R+2sin冊/3/R= 0;丂rot(H_)_冊=0
奜偱偼丂rot(H_)_R= 0;丂rot(H_)_兤= –2 ido sin冊/3/R+2sin冊/3/R= 0;丂rot(H_)_冊=0
偲側傝揹棳偑柍偄偲偙傠偱偼帴応偼塓側偟偱偁傞偲偄偆忦審傪枮偨偟偰偄傞丅(佪D_/佪t=rot H_-i_偱佪D_/佪t=0丆i_=0)
師偵嫬奅忦審傪峫偊偰尒傞偲嫬奅柍尷墦揰偱帴応偑0偱偁傞偲偄偆忦審傪傕偪傠傫枮偨偟偰偄傞偟
撪偲奜偺嫬奅偱偁傞僐僀儖偱嶌偭偨媴柺偺強R = a偱峫偊偰尒傞偲
撪偱偼 H_R = 2 ido cos冊/3; H_冊= –2 ido sin冊/3
奜偱偼 H_R = 2 ido cos冊/3; H_冊= ido sin冊/3
偲側傝帴応偺媴柺偵捈岎偡傞惉暘H_R偑撪偲奜偱摍偟偄偲偄偆忦審偑枮偨偝傟
揹棳偺懚嵼偡傞憌偺岤偝(佮揹慄偺懢偝)傪嚈偲偡傞偲帴応偺媴柺偵暯峴側惉暘H_冊偑
憌偺奜偱ido sin冊/3丄憌偺撪偱–2 ido 倱倝値冊/3偱偁傞偐傜憌撪偺帴応偺兤曽岦偺塓搙偼
rot(H_)_兤= ido(sin冊/3–(–2sin冊/3))/嚈= ido sin冊/嚈
兤曽岦偺柺愊偁偨傝偺揹棳枾搙傪i_兤偲偡傟偽
i_兤=rot (H_)_兤偐傜
i_兤=ido sin冊/嚈
偲側傞偐傜揹棳偺懚嵼偡傞憌偺岤偝嚈偵偐偐傢傜偢
id=嚈 i_兤=ido sin冊
偲側偭偰戣堄偺嬓偁偨傝偺揹棳枾搙偲摍偟偔(3)丆(4)偑夝偱偁傞帠偑傢偐傞丅
廬偭偰墌拰嵗昗偱偺棳傟娭悢冋偼(3)丆(4)偵r= R sin 冊傪偐偗偰
冋=(1/兪)R sin 冊 A_兤
撪偱偼冋= ido R丱2 sin丱2 冊/3丂丂丂丂
奜偱偼冋= ido a^3 sin丱2 冊/(3R)丂 丂丂
偲側傞丅(^^
椺戣偱1A/m偺揹棳枾搙傪幚尰偡傞偨傔偵偼偳偺掱搙嬥懏媴柺傪懷揹偝偣傞昁梫偑偁傞偐峫偊偰尒傛偆丅
傾儖儈崌嬥摍偺嬥懏斅偱敿宎1m偺媴柺傪嶌傝媴柺偺愒摴偱偺廃懍傪壇偊傗偡偄傛偆偵0亷偱偺壒懍330 (m/s)偱夞揮偝偣傞偲偡傞丅
媴柺偺愒摴晅嬤偱偼1昩娫偵挿偝330 m 偺嬥懏斅偑捠夁偡傞偑嬓1m偱峫偊傞偲柺愊偼330 m^2偲側傞丅1A偼1乮僋乕儘儞/s乯偱偁傞偐傜
偙偺嬥懏斅偺拞偵懚嵼偡傋偒揹壸偼1僋乕儘儞丄偟偨偑偭偰愒摴晅嬤偱偼1/330丂乮僋乕儘儞/m^2乯偺揹壸枾搙偱偁傞昁梫偑偁傞丅
媴柺偱偼揹壸偼斀敪偟偁偭偰媴柺忋偵堦條偵暘晍偡傞偲偄偆惈幙偲敿宎1m偺媴柺偺柺愊偼4兾乮m^2乯偱偁傞帠偐傜慡懱偺揹壸検Q偼
Q=4兾/330=0.038丂丂乮僋乕儘儞乯
揹壸Q傪敿宎a(m乯偺媴柺偵梌偊傞偲偒揹埵冇偼恀嬻偺桿揹棪傪兠侽偲偟偰
冇=Q /(4兾兠侽 a)偱梌偊傜傟傞偐傜
冇= (4兾/330)/(4兾兠侽 a)= 1/(8.854亊10^-12亊330亊1)= 3.422亊10^8 (V)
3壄.4愮枩儃儖僩偵側傝幚尰偼傓偮偐偟偄帠偑傢偐傞丅
偦傟偵懳偟偰捈宎1噊偺揹慄偵1A偺揹棳傪棳偡帠偼梕堈偱偁傞偐傜媴柺偵揹慄傪姫偄偰揹棳傪棳偡曽朄偱偼1000丂A/m偺揹棳枾搙傕
梕堈偱偁傞丅
夞揮懷揹媴柺廃曈偺帴応偺奊
偒傢傔偰娙扨側娭悢偱昞傢偝傟傞丅(^^
墌摏宍僐僀儖廃曈偺帴応偺奊(偦偺2) 3 敄偄墌斅僐僀儖丄4岤傒偺偁傞墌摏僐僀儖傊