分岐図を選ぶ基準、最節約、あるいはオッカムの剃刀とは何か?。
データが指し示す仮説を発見せよ 有効な証拠の数は最大に 余計な仮定は最小に
ミラ:最節約とかオッカムの剃刀とか、それはいったい何なの?
わらし:前のコンテンツと少し重複するけど、ようするに余計な仮定は最小限にしろ、そういう決まり事のことね。
ミラ:余計な仮定? なんか分からなくなってきたぞ。さっきは証拠の数が多い方だと・・・・
わらし:まあ落ち着け。さてはて、最節約という考えには非常に長い歴史があるし、基本は同じでも学問のジャンルによってそれぞれ少し違う装いで使っているかもしれんな。ともあれ、話を限ればさっきも言ったようにホモプラシーの数が最小限で成立する分岐図をチョイスせよ。これが分岐学における最節約の使い方だ。あるいは
”同じデータを説明できる場合、進化上のイベントの回数がなるべく少ない分岐図の方を選びなさい”
そういう基準のことさ。例えば先のように2つの分岐図がある場合、
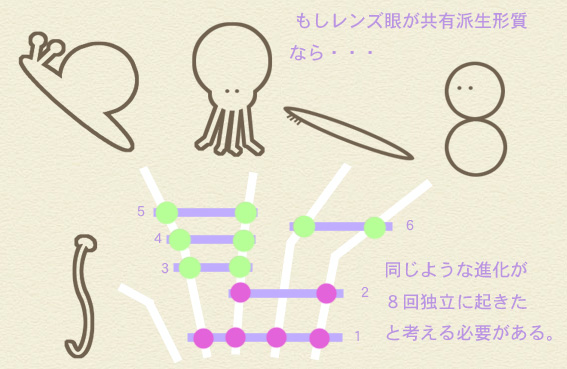
4つのホモプラシー、8回の独立した進化上のイベントが起きなければ成り立たないこの分岐図よりも・・・

1つのホモプラシー、2回の独立したイベントですむ分岐図の方を選ぶ。そういう基準だよ。
ミラ:ふーん・・・・
わらし:なにか疑問がありそうだな?
ミラ:うん。なんていうかな、分岐学では分岐図をそういう基準で選ぶのは分かったわ。それはいいわよ。そういう基準で選んでますってことだからね。知りたいのは”なんでこの基準を使うことにしたのか?”ということよ。それに仮定を少なくという要求が証拠の数とどう関係してくるか。
わらし:それを知りたいと?
ミラ:当然。
わらし:そういうからには最節約の効用も知りたいんだろうな? 最節約が何の役に立つのか? 最節約の基準とはそもそもなんなのか?
ミラ:そうね。それも知りたいわ。
わらし:まあ結論からいうと最節約っていうのは推論における常識的な基準だな。日常的にオラ達がやっていることでもある。
ミラ:はあ? 常識??? なんだよそれ??
わらし:まあな、科学の世界で常識なんて言われたら不安になるよなあ。なにもかも一気に説明できないから順々に話していくだぞ。さっき例え話をしただな。おめーのおやつが食べられていて、現場にはオラの足跡があり、おやつにオラの歯形が残っていたという。
ミラ:したわね。
わらし:なんで犯人がオラだと思った?
ミラ:だってあなたの足跡が残っているのならあなたがそこに来たってことよね? 指紋もあるし、おまけにかじった痕があなたの歯形に一致するのよ。あんたみたいに頑丈な犬歯を持っている子供なんて他にいないと思うし。
わらし:そうかあ? 犬歯の丈夫な小さな女の子がオラの他にいて、その子がおめーがいない隙に忍び込んでかじったかもしれないでねーか。指紋もたまたま似ているだけだろ。
ミラ:そんな子がいるとは思えないし、いてもたまたまあたしの部屋に入るわけねーだろ。というかそもそもそれがお前だ!!
わらし:もしかしたらでっかいネコかもしれねーぞ。
ミラ:そんなのいるか!! だいたい指紋はどうなる?
わらし:そうか? おめーは地球上のすべてのネコを確認したわけじゃあるまいよ。いるかもしれんぞ。4丁目の空き地にでっかいネコが住んでいて、ミラの部屋とおやつを常日頃から虎視眈々と狙っていたのかもしれん。しかも肉球に指紋のような模様が。
ミラ:おいおいおいおいおいおい・・・・
わらし:あるいはチュパカブラかもしれんぞ。あれなら小さいし、牙が生えているし、おおっ、チュパカブラこそすべての証拠にぴったり合うでねーか。化け物だけに指紋の擬態もできるって案配だ。さすが妖怪変化!! 恐ろしや。オラにおやつ泥棒の濡れ衣を着せるとは許せん!!
注:チュパカブラ 近年南米に現れるという怪物のこと。2本脚で歩き、背中に棘のような剛毛をはやし、大きな眼と牙の生えた姿をしている。家畜を襲うともいわれ、話からするとどうも大きさは小さいらしい。いわゆる都市伝説の類いで宇宙人とされるイーバやグレイとも似ている部分があり、たぶん、彼らから派生したミームかなにかだと思われる。以前、雑誌上でチュパカブラの死体だというミイラ写真が掲載されたことがあったが、見た限りではあからさまにネコだった。
ミラ:ふざけるのもいい加減にしろよ。すべての証拠はあんたがあたしの部屋に来たこと、そしてあんたがおやつをかじったことを示しているのよ。
わらし:単純すぎる推論じゃねえ? それ?
ミラ:単純というよりも素直と言って欲しいわね。
わらし:まあな、真面目な話に戻すとこれが日常的な最節約ってわけだな。
ミラ:はっ?
わらし:ミラちゃんは今、犬歯の大きな女の子がいてそれがミラちゃんの部屋にはいってつまみ食いするとか、でっかい未知のネコとかあるいはチュパカブラが存在してそれがやってきた、そういう仮定をことごとく無視したわけだよな?
ミラ:まあね・・・・。えっ、これが余計な仮定をはぶけってことなの?
わらし:そういうこっちゃ。そしてこの場合、証拠から導きだされる余計な仮定の最も少ない仮説とは何か? それは、
オラがミラの部屋に忍び込んでつまみぐいをした
というものだな。犬歯の大きな女の子説とか巨大ネコ説、チュパカブラがつまみぐいした説は、これらが成立するにはあまりにも多くの仮定が必要になってしまうだよ。特殊な特徴を持った女の子がいて、それが忍び込んだ、巨大なネコがいる、都市伝説の化け物が存在している、そういうさまざまな仮定がなければ成り立たない。そういうわけでミラちゃんはこれらの仮説をチョイスしなかったわけだ。
ミラ:いやあ・・・あたしそういう基準で仮説を選んでいたかなあ? なんか実感ないんだけど・・・。
わらし:おめーがデートで待ち合わせをした時、相手が遅れたら何があったんだと思う?
ミラ:寝坊したか身支度で時間がかかったんでしょ? 困った男だなそいつ。
わらし:あるいは電車が遅れるとかな。
ミラ:まあそういうところでしょうね。
わらし:来る途中で事故に巻き込まれたとか、財布を忘れたので一回家まで戻ったとか、そういう仮説はチョイスしないわけだな?
ミラ:まあ、確かに選ばないわねえ・・・・・
わらし:ほら、仮定の少ないシンプルな仮説の方を選んでる。
ミラ:いやあ、事故だの財布をとりに戻るだの、そんなことは普通、経験的に起きにくいと思うからそう考えているだけなんだけど・・・。
わらし:これまで経験的にそうだったからこれからもそうだろう。そういうわけだな?
ミラ:そうね。
わらし:ようするにだ。どういうわけか立て続けにさまざまな事件が起きるとか、それぞれの事件が起きる確率が大幅に変化してこれまで起ったこともない事柄が発生する、そういう日常からはあまり想定できないような余計な仮定を取り込んだ推論はしない。そういうことだな?
ミラ:むむむむ・・・・
わらし:最節約っていうのはな、人間が普段から使っている推論の方法なんだよ。例えばパズルがそうだ。
ミラ:はっ? パズルのどこが最節約なのよ?
わらし:次のようなパズルがあるとするだ。これは別のコンテンツ、詭弁に関する事柄で使ったものなんだが・・・・、ともあれ、

このパズル、ある町の道路の地図を切り刻んだものなんだけど、全部のピースがそろっていないから完全にはくっつかない。ともかく次の2つの組み合わせ方をしてみるだ。
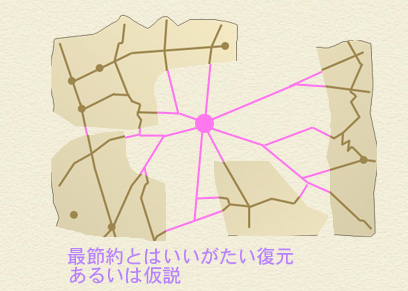

ミラ:ピンク色の部分はなに?
わらし:手に入れられなかった部分の道路を復元したものだ。ここはこうつながっていたのかもしれない、ここにこんな道路があったのかもしれない。それを描いたってわけだな。いわば”もしも道路”ってわけだ。さて、おめーならどっちの組み合わせを選ぶね?
ミラ:右側のこれね。

わらし:なんで?
ミラ:いや、素直にこれだろ?
わらし:ほら、シンプルな方を選んでる。
ミラ:シンプルな方というか、うまく組み合わさっている方を選んでいるだけよ。
わらし:うまく組み合わさっている方を選ぶ、ということは証拠の多い方を選ぶってことだよな?
ミラ:そうかしら?
わらし:地図に描かれた道路を手がかりに組み合わせたんだろう? うまく組み合わさるということは道路がうまくつながっているということ。それは道路という手がかり、つまり証拠がうまく整合する方を選んだってことだ。
ミラ:言われればそうか・・・・・。
わらし:そして証拠が多いってことは言い換えれば、”証拠じゃなくなってしまう手がかりの数は最小限にしろ”ってことなのよね。
ミラ:手がかりが証拠じゃなくなる??
わらし:つながっていない道路は証拠と見なされていないわけだろう? ほら、手がかりが活用されていないだよ。
ミラ:そうねえ。あれ? じゃあようするに最節約とは証拠を素直に有効活用しろってことなわけ?
わらし:そういうこっちゃ。だからこそこちらの組み合わせは最節約な基準では選ばれないわけだよ。

証拠である道路の多くがうまくつながっていないからな。証拠が有効活用されていないだな。
ミラ:証拠が少ないからこの組み合わせは選ばれないというわけね。
わらし:より正確にいえば”せっかくの手がかりの多くを無視しないと成り立たない組み合わせ”だからダメだってことだな。少なくとも最節約な基準ではそう評価されるだな。
ミラ:つまり常識的な判断ということになるわけか。
わらし:そうだ。さらに説明しよう。仮定は最小限にせよ、それが最節約だ。だがそもそも仮定とはなんぞいや?
ミラ:なんでしょうねえ?
わらし:この場合、それは”もしも道路”だな。”もしも道路”が多くて画面上でピンクが多い、それは証拠を無視した結果なんだよ。
ミラ:なんで?
わらし:素直に地図にある道路同士をくっつければいいのにそれをしなかった。だから”もしも道路”が必要になるだな。
ミラ:そうなの?
わらし:無視する道路の数が増えるとどうなる?
ミラ:うーーん、そうねえ。つなげなきゃいけない道路が増えるから必然的に”もしも道路”は増えるわね・・・・・。そうか、無視によって証拠どうしの不整合が生じる、だから・・・・。
わらし:だから不整合を繕わなければならなくなる、そのためにはどうする?
ミラ:そのために”もしも道路”をやたらと導入しなければならなくなる。そういうわけね?
わらし:そういうこっちゃ。そして”もしも道路”こそ”組み合わせを成り立たせるために必要な仮定”なのさ。
ミラ:”もしも道路”が仮定になるわけ?
わらし:こういう組み合わせをしたら道路はこうつながっていただろう、そういうことだろ?
ミラ:それは仮定というよりもむしろ予測じゃないかしら?
わらし:予測でもあるかもな。でも同時にこの組み合わせを成り立たせるには”ここにこういう道路があったとしなければならない”ということなわけだろ? これは仮定でもあるわけさ。
ミラ:むう。
注:”もしも道路”を導入する代わりに道路がそこで切れていると仮定することもできますが、この場合は”もしも道路”の代わりに”ここで切れてますという仮定”を導入することになるので結局は同じ。
わらし:証拠を無視すると”もしも道路”のような仮定を多く導入しなければいけなくなる。なんでそんなことをするのか? もっと少ない数の仮定で十分説明できるのに、もっとたくさんの証拠を有効利用できるのになぜそうする? 証拠をつぶしてしまうような余計な仮定は必要最低限にしろ。仮定は可能な限りそぎ落とせ。”もしも道路”のような仮定が最も少なくてすむ仮説を選びなさい。これが最節約(オッカムの剃刀)という基準の根幹なんだよ。
ミラ:そしてそれは証拠を有効利用することでもあるわけね?
わらし:そういうこっちゃ。仮定の数を最小にするということは有効利用できる証拠の数を最大にすることでもある。ようするに、
仮定の数が最小→無視する証拠の数が最小→なるべく多くの証拠を有効活用できる仮説がベストな仮説
というわけさ。
ミラ:証拠の多い方を選べ→無視する証拠の数はなるべく少なく→仮定の数は最小に、それが最節約であると。
わらし:そうだな。これはなんのこっちゃない。データが最も強く指し示す仮説を選びなさい、ということなのさ。
ミラ:まあ、当たり前ね・・・・。わたしもおやつに残った歯形や部屋の足跡というデータがあったら、それはあなたがつまみ食いをしたという結論を示していると思うわ。
わらし:そうだな。最節約というのは知ってみればどうってことのない基準なんだよ。
ミラ:だから常識?
わらし:そう常識。まあ、あれだな、最節約を否定する人はパズルを組み立てられないだろうな。
ミラ:そうなるのかな。
わらし:たぶんね。演繹や帰納でパズルが組み上げられるとはあまり思えん。最節約とは我々が日常行っている動作なのさ。これ抜きではなにもできないだろうな。
ミラ:そういうことになりそうねえ。じゃあこれを適用したのが分岐学の最節約なのね?
わらし:そういうこっちゃ。まあ、日常やられていることだから多分、自然に適用されただな。でもな、分岐学が出現してさらに研究者達が最節約という基準を使い始めた時、とてもたくさんの疑問や反論が巻き上がったんだ。そういう嵐は研究者の間でこそとっくの昔に過ぎ去ったが、今でも分岐学に始めて触れた人の間にはわき上がるものでもある。何度でもね。
ミラ:へー? なんでそうなるわけ?
わらし:そうだなあ。日常と分岐学における最節約がどんなものかは分かっただな。じゃあ今度はその効用やら疑問やら、あるいは誤解やらもろもろを見ていくか。
参考文献として:
「系統分類学」 E・O・ワイリー 宮正樹・西田周平・沖山宗雄共訳 1991 文一総合出版
「生物系統学」 三中信宏 1997 東京大学出版会
「種の起源」(上下) ダーウィン 原著1859 岩波文庫
分岐学の入門書(のつもり)「恐竜と遊ぼう」はこちら^^;)→