最節約に対する疑問:世界は最節約なのだろうか?
ミラ:でっ、最節約に対する疑問って何ね?
わらし:例えば曰く、進化は最節約に起きているわけではない。だから進化の歴史を推定する基準に最節約を使うべきではない。
ミラ:むう・・・・
わらし:ようするに間違った進化的な仮定を置いているから間違った推論方法であるという疑問だな。
ミラ:どうなのかしら? 納得できるような、よく分からないような・・・・
わらし:これを身近な例に言い換えればこうなるな、曰く、
世界は最節約に振る舞っているわけではない、ゆえに最節約な判断は間違っている。
ミラ:??
わらし:デートに彼氏が遅れた理由はおそらく寝坊であろうとか、あるいは身支度に時間がかかったのであろうという推論は彼氏も含めたこの世界が最節約に振る舞うことを前提にしている。しかし世界が最節約であるとは限らない。そうだな?
ミラ:ええっと・・そうですか? よくわからんのですが。
わらし:この世の中で起きる現象が、いつもいつも最短経路で起きる現象か? 世の中では時々、複雑怪奇なことが起きるだろう?
ミラ:そうねえ。
わらし:ではこのように世界が絶えず最節約に振る舞っているわけでないことは明らかだ。故にデートで彼氏が遅刻した原因を単純な基準を用いて推測することは間違いである。前提がおかしいからな。
ミラ:いやあ・・・・・その、そうかあ?
わらし:まあ、少なくとも最節約に反対する人の意見をまま日常の最節約に適用したらこうなるだろうな。
ミラ:分かるような分からんような。納得できるような納得できないような・・・・
わらし:そうだな。確かに現象が絶えず最短経路で起きるとは言えないよな?
ミラ:まあそうねえ。
わらし:そういう点は正しいだろうな。
ミラ:じゃあこの疑問は正解?
わらし:うんにゃ。例えば彼氏がデートに遅れた時、ミラちゃんは最もシンプルな可能性だけを認めて、他の仮説を一切合切、そのすべてを否定したか?
ミラ:ええっとつまり?
わらし:ミラちゃんは最節約に判断したそれはいいさ。でも最節約に判断したからといって最節約ではない他の可能性、例えばだな、、、、
1:事故によって電車が大幅に遅れている
2:彼氏は財布を忘れたことに気がついて家に取りに帰りました、あいつときやがったら携帯に連絡も入れやがらねー最低な男です
3:彼氏はすっころんで足首をねんざしてひいひい言っておりデートどころではない
4:彼氏は車にはねられたあげくに頭部を強打してただいま記憶喪失中 私は誰? ここはどこ?
そういういろいろもろもろな可能性を絶対ありえないとしたか?
ミラ:いやその、後半は怪しげですが、前半のような事はありうるかなあーとは思いますよ。もしも私が心配性なら事故に巻き込まれちゃった可能性まで考えて大慌てになるかもしれないし・・・・。さすがに記憶喪失とかは無いとは思うけどさ。
わらし:でもそういう事象もありえないわけじゃないよな?
ミラ:そうねえ、ありえないわけじゃないわね。
わらし:まあここから分かるように、最節約という基準は最節約でない推論や仮説を推奨はしていない。だけど、それらをありえないと全否定しているわけでもないのよね。
ミラ:そうね、ないわね。ようするに最節約以外が全部だめ、いっさい認めない、最節約でない現象なんかありえない。そんなことは言っていないわけよね・・・・・・。うーん、だとしたらさっきの批判、つまり最節約でないから最節約は間違っている、これはちょっとおかしくない?
わらし:おかしいだな。ようするに、、、
Q:最短経路で起きるとは限らないじゃないか!!
A:誰も最短経路でしか現象が起きないとは言ってないだろー
こういうわけだな。
ミラ:ようするに批判のピントがずれているのね?
わらし:うんだ。誰もそんな主張はしていないだよ。ようするにあれだな。仮定は最小にしたが、現象が最小であるということを主張しているわけではない。そういうこっちゃ。ちょっと難しい話だがな。
ミラ:じゃあこの批判は間違いなのね?
わらし:半分は間違いだがよ。というか、それはどういう風に疑問を提出したかによるな。それによっては最初の疑問はたわ言とも受け取れるし、あるいは系統学的にも哲学的にも深淵な、そして当然の問いだとも言える。
ミラ:はっ??
わらし:最節約という基準はいわば仮説を選ぶ基準なわけだ。最節約以外の現象や仮説がありえないといっているわけではない。だから
”最節約という基準は日常世界や進化が最節約に進むというありえない前提を敷いている不適切な基準である”
という批判は的外れだ。それはその通り。
ミラ:じゃあ間違いじゃない。
わらし:でもこうも思わないか? なるほど確かに我々は世界が必ず最短経路をとるなどとさらさら思ってはいない。しかしながら系統推定であれ、日常であれ、最節約という基準を用いる時。我々は世界がある程度シンプルに振る舞うという前提までも必要としていないのだろうか?
ミラ:えっ??
わらし:視点を変えて考えてみよう。世界の様相がある日変わった。ありとあらゆることが起る世界。最節約でもなく、シンプルでもなく、これまではあまり起きないと思われていたことが絶えず猛烈な頻度で起きる世界だとしよう、そういう世界でも最節約な基準はなおも有効だろうか?
ミラ:うううーーーんんんん、なんか直感的には有効でないような・・・・・。
わらし:まあ、直感的には有効ではないように思えるな。だとしたらこういうことが言えそうだ、
:最節約な基準を用いる時、それは最節約とまでは言わないまでも、世界がある程度はシンプルに振る舞うことをやはり前提にしているのではないか?
:世界がそこそこシンプルに振る舞うからこそ最節約という基準が有効なのではないか?
:分岐学の正しさも生物の進化の振る舞いがきっちり最節約でございますとは言わないまでも、やはり比較的シンプルに進むことに依存しているのではないか?
どうだ?
ミラ:むむむむむむむ・・・・・????
わらし:じつはミラちゃん自身も暗に自然に対して確率を組み込んだ意見を言っているのよね。
ミラ:へっ? いつ言った?
わらし:前のコンテンツで言っていたでねーか。
「いやあ、事故だの財布をとりに戻るだの、そんなことは普通、”経験的に起きにくい”と思うからそう考えているだけなんだけど・・・。」
ってな。これ明らかにある現象が起きる確率について申し述べたものだろ。しかもあからさまに”確率は少ない”っていうのと同じ内容を言ってるぞ。ようするに世界がある程度シンプルに振る舞うことを前提にしているってわけさ。
ミラ:むむむっ、でもさ、これって普通な考えじゃない? 例えばよ、彼氏が事故に合う可能性は小さい、事故で記憶喪失になる可能性も小さい、じゃあ彼氏が事故に合って記憶喪失という出来事が起きる確率はもっと小さい、だったらそういう仮説はチョイスしなくていいだろう。これって普通よね?
わらし:逆にいうとなんだかんだいって人間は世界がシンプルに振る舞うと仮定しているってことだな。
ミラ:うーーーむ。じゃあ、最初の質問をちょっと言い換えるわよ。分岐学が正しい答えを見つけるには進化がどのくらいシンプルに進めばいいわけ? どこまで進化がシンプルに振る舞うと仮定しているのかしら? 例えば共有派生形質ではないけど見た目は似ている特徴、あれなんていったっけ?、、、、、
わらし:収斂とかホモプラシーのことだな。
ミラ:そうそう。そのホモプラシーがたくさん起きたりしたらどうなるの?
わらし:ホモプラシーは系統を反映していない現象だよな?
ミラ:そうだわね。
わらし:そういう”現実と異なる系統を示す情報”が増えたら系統推定は間違うこともありうる。そう考えることはできるよな。
ミラ:できるわよね。
わらし:こんな事例を考えよう。ここにA、B、Cという生き物がいるとするだ。これらの系統関係は、
______外群
|____A
|__B
|__C
というものであったとする。
ミラ:BとCが姉妹グループなのね?
わらし:そういうこっちゃ。括弧で表せば A(B C) だな。それらが進化する過程で次のような形質の進化があったとする。
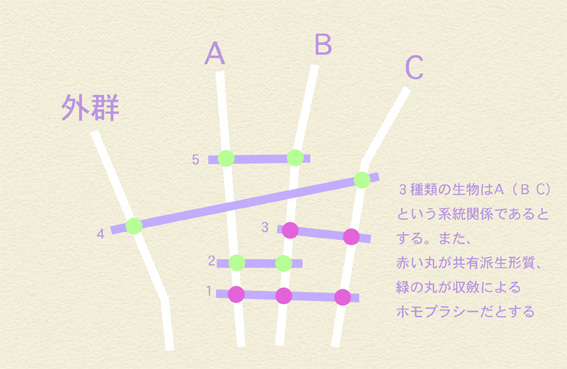
ミラ:赤い丸が共有派生形質、緑が収斂で生じたホモプラシーってわけね?
わらし:そうだ。ホモプラシーが多いよな?
ミラ:そうね。
わらし:でっ、外群比較するとこうなるだな。2と5は収斂なのに一見するとAとBを束ねる共有派生系質に見えるだよ。
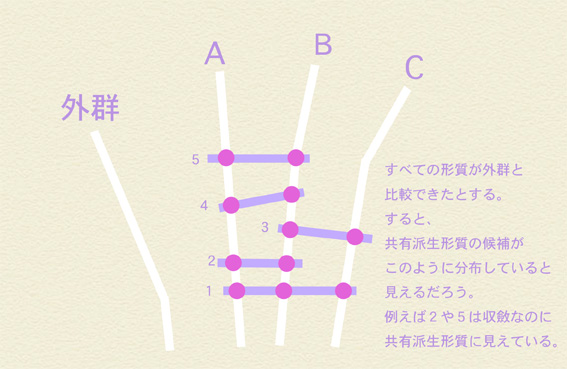
ミラ:タコと人間のレンズ眼のようなものなのね?
わらし:まあな。
ミラ:ところで4の特徴がAとBを束ねる共有派生形質の候補になっているのはなんで? 外群とCで収斂した形質のはずでしょ?
わらし:外群比較では外群が持っている特徴が原始的であると仮定して比較するだろ? この場合は外群で派生形質が産まれちまったから、それと比較すると本当は原始形質なのにAとBが持つ特徴4がAとBを束ねる派生形質に見えちまうだよ。
ミラ:へー、そういう誤認も起るんだ。
わらし:まーな
注:外群比較は外群が原始形質を持っていると仮定して派生形質を見つける方法ですが、外群の持っている特徴のすべてが原始形質とは限りませんので、場合によるとこういうことが起ります。とはいえ、この問題はより多くの外群を見つけて比較することで解決できる問題でもあります。ようするに外群それ自体が妥当なチョイスであったのか検証するってわけですね。ちなみに北村の著作、「恐竜と遊ぼう」ではコエルロサウリアの派生形質をあぶりだすためにアロサウルスを使いましたが、そのなかで”アロサウルスのクアドレートとクアドレートジューガーの間にある穴が小さい”を原始形質と仮定して、コエルロサウリアの”クアドレートとクアドレートジューガーの間にある穴が大きい”を共有派生形質とカウントしています。じつはこれ、この手の誤認なんですよね(ただしこの場合のこれは話を単純化するため意図的にやったこと)。実際には他のさまざまな獣脚類を加えて検討するとだんだんわかってきますが”クアドレートとクアドレートジューガーの間にある穴が小さい”は原始形質ではなく、むしろアロサウルスなどを含むカルノサウリアの共有派生形質です(クアドレートのフランジが大きい、とも表現される)。外群比較で示された派生/原始というものはあくまで仮説的なもので、それで系統を編んだ後でも、なおそれ自体が検証すべき課題であることはお忘れなく。さりとて、仮説的だから間違いだってわけでもありません。もしそうなるのなら私たちがよってたつこの世界の様々な事柄が間違いだということになるでしょう。
わらし:まあ、ともあれだ。この共有派生形質の分布を用いて分岐図をつくるとこうなるだな。見ればわかるがAとBが姉妹群であることになっているだ。ようするに間違いだってわけだ。
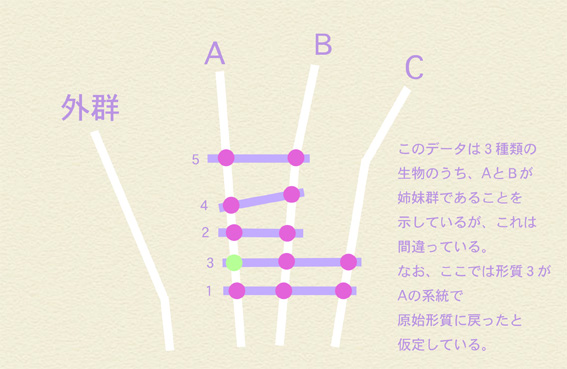
ミラ:ふーん、ホモプラシーが多くなるとやっぱり間違えるんだ。じゃあ、やっぱりさっきの質問は少しは当たっていることになるわけ? 分岐学はホモプラシーがたくさん起ると、つまり進化がシンプルに進まないと間違えてしまう、そういうことなのかしら?
わらし:まあ間違えることはありうるな。
ミラ:じゃあ無効なの?
わらし:それがそうとも限らんのだな。
ミラ:へー? どうして?
わらし:例えば次の事例を考えてみよう。
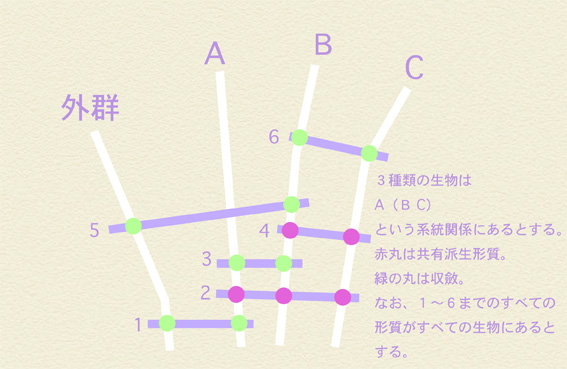
これはホモプラシーをさらに多くしたものだ。さて、この場合に外群比較してみると共有派生形質かな?と思われるものは次のような分布になるだよ。

ミラ:形質3と6は収斂が共有派生形質に見えちゃっている例なのね。この場合、形質3はAとBが姉妹群であることを示していて・・・・、あれ? 形質6は収斂なのにBとCが姉妹群であることを示しているのね。
わらし:うんだ。そして形質1と5はこれまた原始形質が派生形質に見えちまっている例だな。
ミラ:形質1はBとCが姉妹群であることを支持しているわけね。
わらし:そうだな。そして形質5はAとCが姉妹群であることを支持している。これらお互いに矛盾するデータ。それを全部考慮すると・・・・

こうなるだ。これ、正しい系統が導きだされるんだよな。
ミラ:はへーー?? なんか不思議ねえ? ちょっとご都合主義な気もするけど。
わらし:ご都合主義っていったら先に例として出した正しい系統が編めなかったものもそうだぞ。BとCが姉妹群であるという正しい解答を示す共有派生形質を無効化するために、AとBが姉妹群であることを支持するホモプラシーを2組みと、さらにAとBが共有する派生形質に見えるような原始形質をわざわざ1組導入しているからな。あれはあれで正しい系統を編めないようにする状況をご都合主義的に考えたもんでしかないだよ。
ミラ:うーーーん、そうかあ。じゃあ、あれね? ホモプラシーが多いからといって正しい系統が推論できないわけじゃないのね?
わらし:そういうこっちゃ。ホモプラシーや進化のイベントが多ければ正しい推論ができないに違いないという人もいるが、それは単純すぎる考えだな。本当の共有派生形質が示す系統を破壊するような分布をホモプラシーが示す場合もあるし、逆の場合もありうる。例えばホモプラシーの分布によっては系統解析をまどわせるホモプラシーが見かけ上、原始形質に見えてしまってデータからはじかれる場合もありうるだろうな。
ミラ:へー? それはどんな?
わらし:例えばBとCが近いということを支持しないホモプラシーがAとBで発生したとする。ところがこれが外群でも起きた。もしそうなったら外群比較をするとAとBが近いことを示す見せかけの形質が派生形質としてカウントされないことになるだな。これなんかはホモプラシーが少ないとむしろ起きにくい現象かもしれん。
ミラ:なるほど。
わらし:でも間違えることもありうる。今見てきたようにね。
ミラ:そうねえ・・・・。ようするに間違える状況を考えることも。正しい答えを導ける状況を考えることもできるってわけね。
わらし:そういうこっちゃ。ここから次の事がいえる。
:分岐学は進化が最節約に進まない状況やホモプラシーが多発している状況では必ず間違えるから使えない。これは正しくない
ミラ:そのような状況で間違えることもありうるし、正しい答えを導くこともありうるからなのね。
わらし:そういうことね。だが疑問は残るだよ。それは分かった、では・・・
:ではどの程度、間違えるのだろうか? また実際の進化はどのようにふるまっているのだろうか?
:実際の進化で起きるホモプラシーはどのくらいの量なのだろう?
:実際の進化でおきるホモプラシーの量は最節約による系統推定にどんな影響を与えるのだろうか?
:分岐学はさまざまな状況でどの程度正しい答えを導けるのだろうか?
こういう疑問が次に出てくる。
ミラ:うううーーーむむむ、単刀直入に聞いちゃうけど、実際、どのくらい影響を受けるものなの?
わらし:その問いに対して答えるのは難しいだな。さっきの例え話もご都合主義ともとれる事例を2つ提案してみせた、というだけだからな。じつは最節約を否定する人も肯定する人もこの問題を長年検討してきたが十分に解決したとは言えない状況にあるだな。現実は最節約じゃないから最節約はだめな基準に違いない、というナイーブなことをいう人間はさすがにもういないが、今ここで問題にしている問題それ自体の解決はまだすんでいない。
注:このあたりの問題は「過去を復元する 最節約原理、進化論、推論」 エリオット・ソーバー 1988 蒼樹書房 三中信宏 訳 を参考にしてください。正直、これは長年議論されている非常に難しい問題です。
ミラ:じゃあ、じゃあさ。実際の生物の進化はどうなっているわけ? 分岐学が役に立たなくなるような状況が絶えず起っていたりするの? それを知る方法はないわけ?
わらし:すでに系統が分かっている生物のデータを使ってテストしたりシミュレーションしたりすればいいだよ。
ミラ:その結果は?
わらし:分岐学(最節約法)はかなりの確率で正しい答えを導けることがわかっているだ。
ミラ:どのくらい?
わらし:まあ、8割、9割。
ミラ:へー、いいじゃない。じゃあ有効だってことなのね?
わらし:まあそうだな。たださっきの疑問には直接答えたことにならないかもしれんだな。経験的には正しい答えをかなりな割合で導きうる方法であると分かっても、世界の有り様と分岐学が前提にしているかもしれない事柄に関する疑問に完全には答えていないからな。これはいわば肩をすくめて、
”なにもかも分かったわけではないが、少なくとも経験的に役に立つだろ?”
というのと同じようなことかもしれん。
ミラ:いやあ、役に立つ事がわかれば私はそれで十分だと思うけどな。世界の有り様なんかに興味ないし。
わらし:まあそういうな。これは分岐学者も系統学者も科学哲学者にとっても深刻な問いかけでもある。ここには統計学者も1枚かんでくるかもしれんだな。まあ、どっちにしろ世界の有り様まで含めた問いに対する問題解決は先のことだろう。
ミラ:ふーん。
わらし:まあここまできて振り返れば面白いのはむしろ最初の問いかけだな。”最節約でないから最節約は間違いだ”これは興味深い事柄をあぶりだしているともいえる。
ミラ:へー? それは何?
わらし:分岐学にはさまざまな反論、異論が巻き上がった。研究者同士だけではなくて一般の人からもね。分岐学が具体的にどういう手続きと処理をするものなのか分からないのに異論を唱える人は多いわ。最節約じゃないからうんぬん、という発言もそういう流れのなかで歴史上何度も何度も出てきたものなわけよ。なんでだと思う?
ミラ:さあ、、、、なんでかしらね?
わらし:違和感があったからだろうな。さて、どうして違和感を持つんだと思う?
ミラ:はっ? 知らないわよ。
わらし:例えばミラちゃんは始めてみたものに違和感をもつ?
ミラ:いや、、、持たないけど。
わらし:違和感がある。拒否する、異論や反論をぶつける。それは”すでに自分なりの答え”を持っていたってことじゃないかな?
ミラ:ううううーーーんんん、まあ、そういうこともあるでしょうねえ。
わらし:自分なりの答えとはなんだと思う?
ミラ:さあ?
わらし:じゃあ今度は、私たちがどうして分岐学や系統解析に違和感を持つのか? そしてどうしてあらかじめ自分たちなりの答えを用意できていたのか? それを考えていきましょう。
分岐学と人間の認識のコンフリクト→ 工事中
参考文献として:
「系統分類学」 E・O・ワイリー 宮正樹・西田周平・沖山宗雄共訳 1991 文一総合出版
「生物系統学」 三中信宏 1997 東京大学出版会
「種の起源」(上下) ダーウィン 原著1859 岩波文庫
分岐学の入門書(のつもり)「恐竜と遊ぼう」はこちら^^;)→