自然単位系

自然単位
　　光速 c
　　　　3×108 m/s
　　　　長さと時間に関わる。
　　　　特殊相対性理論に関わる。
　　プランク定数 h
　　　　6.6×10-34 J∙s(kg∙m2/s)
　　　　周波数(回/s)を掛けるとエネルギーが求まる。
　　　　　　J(kg∙m2/s2)
　　　　質量とエネルギーに関わる。
　　　　ニュートリノ、電子、クオークに関わる。
　　　　量子力学に関わる。
　　重力定数 G
　　　　6.7×10-11 N∙m2/kg2(m3/(s2∙kg))
　　　　質量2つを掛けて、距離の2乗で割ると力が求まる。
　　　　　　重力＝G×質量1×質量2/距離2
　　　　　　N(kg∙m/s2)
　　　　重力に関わる。
　　　　一般相対性理論に関わる。

この３つは宇宙すべての現象を解くキーとなる

上記の３つの自然単位からプランク単位が求まる。
　　プランク長さ
　　　　これ以上小さくできない長さ
　　プランク時間
　　　　これ以上小さくできない時間
　　　　プランク長さを光が横切る時間

プランク長さとプランク時間はプランク質量から求める。
プランク質量をシュヴァルツシルト半径とプランク定数より求める。

　　シュヴァルツシルト半径
　　　　物質の密度を高めていき、ある半径より小さくなると表面の
　　　　重力が強くなり、光が逃れることのできなくなる。
　　　　その半径のこと。物質の最大密度。
　　　　r = 2Gm/c2
　　　　　　（r:半径、G:重力定数、m:質量、c:光速）

　　プランク定数の式
　　　　E = hν
　　　　　　（E:エネルギー、h:プランク定数、ν:振動数）

　　この２つの式をあわせる。
　　　　「E = hν」の式のν（周波数）を「光速(c)/波長(λ)」に
　　　　置き換える。
　　　　　　E = h(c/λ)
　　　　さらに波長を「半径(r)×π」に置き換える。
　　　　　　E = h(c/(r×π))
　　　　　　　= (hc)/(rπ)
　　　　Eを「mc2」に置き換える。
　　　　　　mc2 = (hc)/(rπ)
　　　　rを左辺に持ってくる
　　　　　　r = h/(πmc)
　　　　このrを「2Gm/c2」に置き換える
　　　　　　h/(πmc) = 2Gm/c2
　　　　mを左辺に持ってくる
　　　　　　m = √((h/2π)(c/G))
　　　　プランク定数をディラック定数に置き換える。
　　　　　　ħ = h/2π

　　m（プランク質量）= √(ħc/G)

この式の意味
　　「ある波長の光子1個のエネルギー相当質量」と
　　「その質量のシュワルツェルド半径」があって、
　　その「波長」と「半径」がイコールになるところ。
　　つまり、波長をどんどん短くしていくと、
　　その質量が増えるため、それ以上波長を短くできない長さ。

プランク単位

　　プランク質量
　　　　2.2x10-8kg

　　　　質量 = √((h/2π)(c/G))
　　　　　　 = √(6.6×10-34/2π × 3×108 / 6.7×10-11)
　　　　　　 = √(4.7×10-16)
　　　　　　 = 2.2×10-8 kg

　　プランクエネルギー
　　　　2×109J (1.3×1019Gev)

　　　　エネルギー = mc2
　　　　　　= 2.2×10-8 × (3×108)2 = 2×109 J
　　　　電子ボルトに換算
　　　　　　(2×109J)/(1.6×10-19J)
　　　　　　=1.3×1028ev = 1.3×1019Gev

　　プランクスケール
　　　　1.6×10-35m
　　　　プランク質量のエネルギーの光子がもつ波長の半径分

　　　　(h/2π）/（プランク質量(m) × c）
　　　　= 1.05×10-34 / (2.2×10-8 × 3×108)
　　　　= 1.6×10-35
　　　　上の式は以下の式から導かれる
　　　　　　波長(λ) = c/周波数(ν)
　　　　　　ν = E/h
　　　　　　E = mc2

　　プランク時間
　　　　5.4×10-44s
　　　　プランクスケールを光が通過する時間

　　　　l/c
　　　　= 1.6×10-35 / 3×108
　　　　= 5.3×10-44

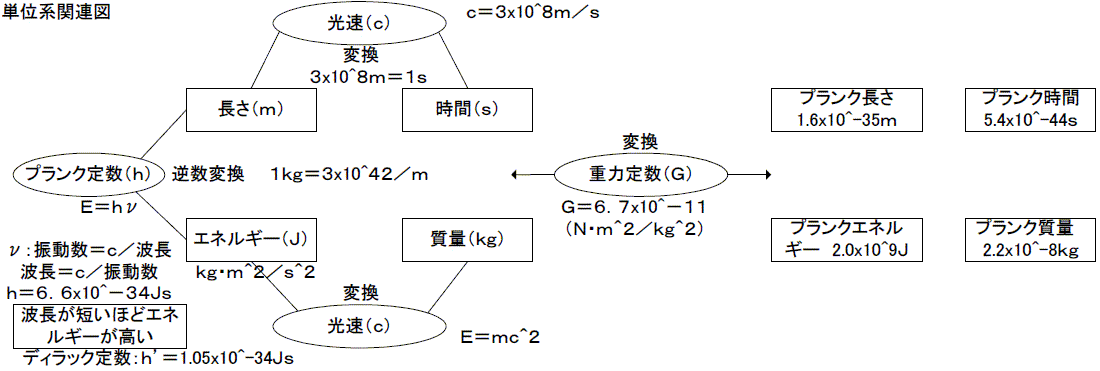
主要単位は光速とプランク定数を通じて関連しあっている。
主要単位とプランク単位とは重力定数を通じて関連しあっている。



参考式
　　物質のエネルギー(kg∙m2/s2)
　　　　E = mc2
　　　　質量(kg)×光の速さ(m/s)2
　　光のエネルギー(kg∙m2/s2)
　　　　E = hν
　　　　プランク定数(kg∙m2/s)×振動数(回/s)
　　位置と運動量
　　　　位置の不確かさ(m)×運動量の不確かさ(kg∙m/s)
　　　　＞　プランク定数(kg∙m2/s)
　　時間とエネルギー
　　　　時間の不確かさ(s)×エネルギーの不確かさ(kg∙m2/s2)
　　　　＞　プランク定数(kg∙m2/s)