生成のメカニズム　

　　　　　　　　　　　　　　＜ギャラリーへ＞　＜面白数学らんどへ＞　＜変換の具体例＞　＜ダウンロード＞

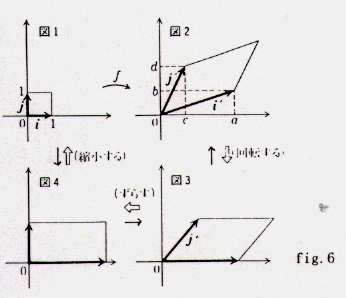
　まず、アフィン変換を説明しましょう。図の ｆ は、1次変換を表します。1次変換とは、簡単に言うと、図のように正方形を平行四辺形に

変形する変換です。これを分解すると、図の↓→↑のように、まず相似縮小（拡大）を行い、ｘ軸方向へのずらしを行い、そして原点の

まわりに回転移動する、というように述べることができます。この1次変換は、行列という数学の言葉で記述されます。

　さて、この1次変換は、原点は原点に移るという変換ですので、ちょっと自由度がありません。そこで、この1次変換にさらに平行移動

を加えた変換を考えます。これを「アフィン変換」と呼びます。アフィン変換は、拡大縮小、ずらし、回転した図形を平行移動して貼り付

ける操作と考えることができます。

　このようなアフィン変換を任意に複数個（通常は2個か3個）作ります。ここで、次のような手順で点を座標平面に次々プロットします。

　　　　　 �@　初期値としてデタラメにある座標（ｘ，ｙ）を選ぶ。

　　　　�A　その点を、準備した複数個のアフィン変換のどれかをデタラメに選んで変換する。

　　　　�B　変換された点を座標平面上にプロットする。

　　　　�C　その点を、また、�Aで行ったように再びどれかのアフィン変換で変換する。

　　　　�D　以下、�B�Cを順次繰り返す。

　このような操作により、変換された点を次々プロットしていきます。このとき準備するアフィン変換を上手に取れば、どんな初期値

から始めても、発散しないある有界な図形の内点上を動き回ります。

　このような、単純で、なおかつ「ランダムな」操作であるにもかかわらず、複雑でユニークな図形が生じるというのが面白いところ

です。

＜変換の具体例＞