ニネヴェ図書館の科学史漫画その6 天動説 後編
周転円、離心円、そしてエカントの導入 天動説はいかに精度の高い理論となったか
紀元150年代にプトレマイオスが理論を完成させた時、天動説はすでに500年近い歴史を持っていた。太陽の運行説明は比較的簡単である。太陽は一年の間にその運行速度を変化させるが、これを説明するには太陽軌道の中心を地球からずらせば良い。つまり離心円を使えば太陽の運行がほぼ説明できる。一方、惑星の運行はそれだけでは無理であった。惑星はいつもは東へ動いているが、ある時、反転して西へ移動し始める。これを逆行と呼ぶ。そして惑星の逆行はやがて終わり、再び元の方向、東へ動き出す(順行と呼ぶ)。
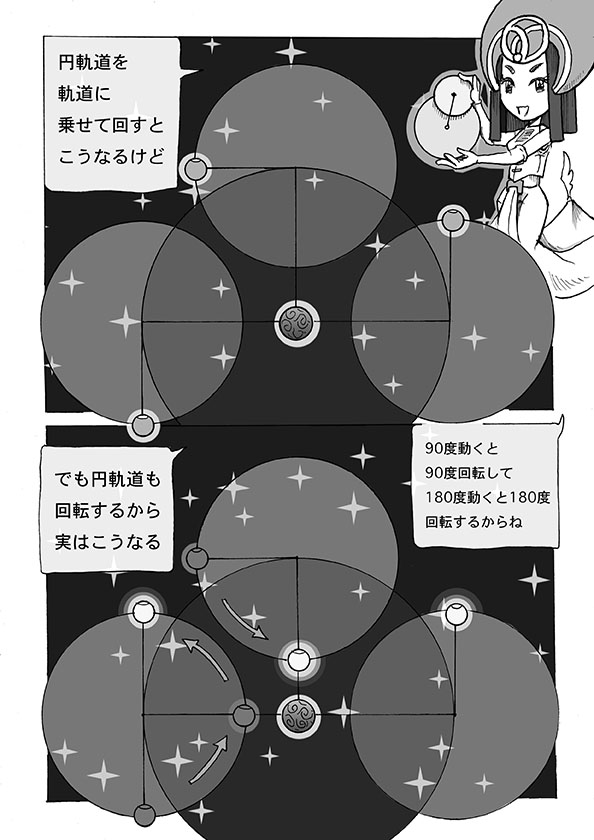
惑星の逆行を説明するために使われたのが周転円であった。周転円は円軌道の上に円軌道を乗せて動かすもので、こうすると惑星は花定規で描いたような、いわゆるサイクロイド曲線で動く。円軌道の大きさをうまく調整すると、惑星の逆行、そのままの動きを再現できた。こうして二つの円運動の合成で惑星の逆行を説明することも可能になった。
しかし惑星の運行は逆行だけではない。惑星もまた、太陽と同様、運行速度を変えるのである。このため周転円と同時に離心円も導入された。例えば火星の軌道の中心を地球からずらす(つまり離心円。)これにより、火星の運行速度の変化を説明する。さらにその火星軌道の上にもう一つ円軌道を乗せて、この組み合わせで逆行を説明する(つまり周転円)。しかしそれでもなお惑星の動き、火星の運行には説明できないずれが生じた。
プトレマイオスに至る天動説500年の歴史の中で、ここまではすでに整備されていた。そして紀元2世紀。プトレマイオスは以上に加えて、エカントを導入したのである。惑星の回転の中心は地球ではない。地球からずらした離心円の中心でもない。惑星の回転運動の中心は地球と離心円の中心、それと同じだけ離心円中心から外れた場所(地球と反対側の場所)にある。こうすると惑星の動きがうまく説明できる。これがエカントであった。すなわち軌道の中心と地球までの距離。その距離と同じだけ離れた場所を回転軸とする。エカントという呼び名は”同じ”を意味するラテン語が由来であり、このエカントの導入によって天動説は高い精度を得ることとなった。
現代人は、エカントはご都合主義と頭から馬鹿にする。そして天動説は精度が低いと思い込む。しかしこれは完全な間違いだ。天動説と地動説は回転軸が反転しているだけで数学的には同じ。つまりその精度は原理的に等しいのである。事実、周転円、離心円、エカントを反転するとそれは現代物理と等しくなるし、エカントはケブラー第二法則の近似値...というか系統的に言うと同一個体であった。
天動説と地動説は数学的に等価である。このことは古代から知られていた、だからもし古代の天文学者たちが現在の地動説、すなわちケプラーによる楕円軌道導入によって、かつての天動説、そして地動説の限界を打ち破った高い精度を誇る理論体系を知ったら、その正確さに驚き、目を見張り、称えるだろう。その一方で彼らは戸惑うはずである。数学的に等しいはずの天動説を一方的に馬鹿にする無知蒙昧な現代人たち。彼らを見て古代人は困惑するだろう。そして思うに違いない。現代人は偉大なるケプラーから生まれた堕落した子孫であり、知的に退化した種族であるのだと。それぐらい私たちの天動説理解は間違ってるし、私たちの知力は古代人の数学能力に遠く及ばない。





















天動説は地動説よりも複雑である。こういう俗説は完全に間違いだ。両者は数学的に等価である。これを踏まえて、高校物理程度の知識を持っていれば、離心円がケプラー第一法則の近似であり、エカントがケプラー第二法則の近似であることは容易に理解できる。さらに周転円は惑星軌道に地球軌道を乗せたものであった。
例えばプトレマイオスが算出した火星の周転円は60:39.5の比率で成り立っているが、火星軌道と地球軌道の実際の比率は60:39.38である。同様に木星の周転円は60:11.5(実際には60:11.53)、土星の周転円は60:6.5(実際には60:6.29)であり、正しい比率とほぼ同じ値が導き出されていた。
地球から見た惑星の動きは、動く地球と惑星の動き、この二つの合成で生じる。天動説では地球を固定するために、地球の動きで生じる”見かけの動き”を惑星軌道に乗せることになった。こうして誕生したのが周転円であり、これゆえに周転円もまた座標を反転すれば地動説と等しくなるのだった。
かようにプトレマイオスの天動説は現在の地動説とほとんど同じであった。違いは軸が反転していること、そして現在の地動説がケプラーの創案で楕円軌道を採用していることにある。つまるところ、もしプトレマイオスが楕円軌道を採用して、エカントをより適切な形式に作り替えれば、現在の地動説とまったく同じ精度を持つ天動説を作り上げることができただろう。つまるところ、楕円軌道の不採用とそれによって生じる誤差を抜かせば、プトレマイオスの天動説は現代天文学に迫る精度を実現していたことになる。これ以上の精度を達成するのは実に17世紀のケプラーであって、それに至るまでの1500年。その長きに渡ってプトレマイオスの天動説が使用されたのは当然であった。
以上の知見を踏まえれば一般的な俗説、天動説は精度が悪かった。天動説は説明するために周転円を次々に導入して複雑になった。地動説の方がシンプルに現象を説明できるという数々の俗説がまったくの誤りであることが理解されるだろう。
天動説と地動説が数学的に等しいものであること、そして高校物理程度の知識を知っていればこんな俗説を信じるはずがない。しかし実のところ、その肝心な高校物理教科書のコラムに、天動説は精度が悪く、説明するために周転円を次々に導入して複雑になったと書かれているのであった。
なんでこんな素っ頓狂な間違いが高校教科書に書かれているのか理解しがたいが、多分、現代の科学者が過去を軽視する性質を持つためではないだろうか。古典を重視した古代、中世の科学と違って、現代科学は古典を破壊することで成立し、成立した理論をさらに破壊してよりよいものを作る。これを繰り返してきた。だから現在の科学者は古典を読まないし、原典も読まない。そもそも読む必要がないのである。実際、業績をあげる上ではこれで十分なのだ。しかし、過去を解説する時には、これは致命的であった。実際、理系の解説者は、ニュートンがニュートン方程式を提案したとか、現在のマックスウェル方程式でマックスウェルの業績を解説するとか、そういう間違いを平気で書いたり、言ったりするものだ。これと同じことが高校物理の教科書で起こった。そして間違いだらけの天動説解説コラムが書かれた、そういうことなのだろう。
端的に言うと、天動説と地動説は数学的には等価なので、どっちが複雑ということはない。むしろケプラー以来の地動説は楕円軌道を採用したので、プトレマイオスの天動説より複雑である。ただしそれは現象を説明する精度を高めた結果であった。そして仮に天動説で楕円軌道を採用すれば、現代地動説と同じ精度が達成されたであろうし、そして現代地動説と同様に複雑な天動説が成立したであろう。
天動説はかように地動説と等価であり、複雑にはなっていない。ただしこれは個々の惑星軌道に関してである。天動説は地球を固定したために、地球の動きで生じる見かけの動きを各惑星に添付することになった。これゆえ、個々の惑星軌道に関して言うと、地動説と天動説はその複雑さが同じであるのだが、全体としては天動説の方が複雑になった。より正確に言うと軌道の数が多くなった。
例えば地球を固定したから地球の公転運動を司る周転円が各惑星軌道に添付された。さらに地球の自転運動で生じる1日一回、西方向へ天体が回転する運動を説明する円運動が各惑星に添付された。このように、地球を固定したがゆえに地球の自転と公転運動が各天体に添付、付与される。こうして天動説は複雑になったのである。しかし、個々の惑星軌道に関してなら天動説の複雑さは地動説と等価であり、精度も変わらない。高校物理教科書のコラムは、この点をよく理解していない。
さらにいうと全体としてなら単純になる地動説も、それはあくまでも天体の運行に関してであった。慣性と落下、その二つの力の合成による運動の説明。こういう知識は古代、中世ではまだ発明されていなかった。そうである以上、古代や中世の物理学では、地球を動かすことによって生じる物理的な困難が多数生じてしまった。要する地動説は、運行は単純になるが物理的に複雑になったのである。いやむしろ、地動説は解決不可能な問題を多産してしまう致命的な欠陥があったと言うべきだろう。
地動説の方が単純で望ましいが物理的困難があるから天動説を採用する。かように宣言したプトレマイオスをはじめ、古代、中世には、天動説と地動説は数学的には等価であることをちゃんと理解した人々が連綿といた。それでも彼らの多くが天動説を選んだのは、地動説の物理的困難を見出したからであった。かような古代人、中世人の理解に比べると、高校教科書のコラムや現代人の俗流理解はまったくもって劣っている。
そしてさらに付け加えると、精度を高めるために無闇に周転円を大量導入した。教科書のコラムと俗説は、これを天動説が行ったと述べているが、これも正しくない、なぜならその最後の試みは天動説ではなく、コペルニクスが地動説で行ったからである。しかもその動機とは精度を高めるためではなかった。哲学的信念が理由なのであった。高校教科書のコラムと、一般の俗流理解は何もかも正しくない。
そしてコペルニクスの地動説は皆が思い、信じるようなものではなかった。コペルニクスの地動説は科学の歴史上、もっとも不可解で得体の知れない出自を持つのである。
参考文献
アルマゲスト 恒星社
ギリシア数学史 T.L.ヒース 共立出版