ニネヴェ図書館の科学史漫画その5(前編)
プトレマイオスによる三角関数の完成
3度の直角三角の比率を求めれば、月、地球、太陽の距離の比が求まる。前3世紀、アリスタルコスによる画期的な試みは、しかし当時の数学の限界に直面した。3度の辺の比を出す方法がないのだ。これゆえにアリスタルコスは18:1以上、20:1以下、という近似値を出すにとどまった。3度の辺の比を求めることに成功したのは実に400年後の2世紀、ローマ帝国統治下にあるギリシャ人、プトレマイオスであった。プトレマイスの方法は五角形から六角形を引き算することで12度の比を求め、それを2回分割することで3度の比を求めるというものであった。このためにプトレマイオスは「幾何原論」をはじめ、当時の数学の全てを導入し、それのみならず、プトレマイオスの定理を発明することでこの計算を行った。そしてこの作業の肝である五角形の作図術。これは実のところ魔法陣研究から誕生したものだったのである。





















アリスタルコスは半月の時、地球、月、太陽が3度の直角三角形を作ると考えた。実際の値は1度の6分の1程度なのだが、それはここでは論じない。しかし、前3世紀のアリスタルコスが使えた数学は「幾何原論」のみであり、これが彼の計算の限界となった。なるほど、「幾何原論」第6巻、命題3を使えば角の二等分ができる。すなわち、三角形の角を二等分すると向かい合う辺が残りの二辺の比率で分割される。45度の直角三角を二分して、22・5度の直角三角と、その辺の比率を求めよ。現在だと高校数学で登場する例題だ。しかし、このやり方では45度=>22・5度=>11・25度=>5・63度=>2・8度となって、肝心な3度の値が出ない。アリスタルコスが近似値を出すにとどまったのはこれが原因であった。
ここから400年後の紀元150年ごろ、ローマ帝国統治下のギリシャ人プトレマイオスは次のようにして3度の比を求めた。
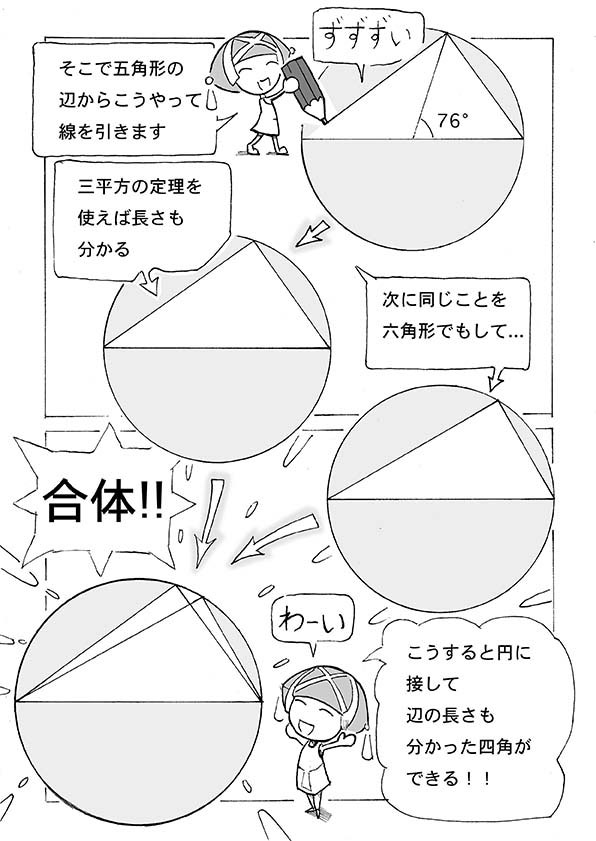
五角形を作る三角は72度であり、六角形を作る三角は60度である。72−60は12であり、12度を2回分割すると3度の比率が得られる。この72−60の引き算を行うために発明されたのがプトレマイオスの定理であった。
さて、この計算には五角形と六角形の辺の比率を知っている必要がある。六角形は簡単だが、五角形の辺はどうすれば求まるのか? ここで使われたのが「幾何原論」第4巻であった。前4世紀に成立した古代ギリシャ数学のひとつの到達点、「幾何原論」には五角形とそれにまつわる命題が幾つもある。そのひとつ「幾何原論」第4巻の命題10。この命題は、五角形を作る三角は分割するたびに同じ三角が出現する黄金三角であること、それは二次方程式で表現できることが示されている。つまり二次方程式を解けば五角形の辺が求まるわけで、プトレマイオスはこれを利用した。
ただし、これは読んだだけではさっぱり理解できないので、アーボーの「古代の数学」110ページ付近を参考にすると良いと思う。とはいえ、アーボーの言っていることも自分には最初まるで理解できなかった。数学の素養がない人間にとって、これら一連の命題を理解するには骨が折れると思う。そして実のところ、これらの命題の真の到達点とは、五角形の作図術であり、ひいては魔法陣作製法であった。
五角形は分割するたびに同じ三角が現れる黄金三角から成り立っている。おそらくこの性質が特別視されて五角形の研究がいくつもなされた。いや、より正確に言うと、古代ギリシャで五角形の研究がされたのは、ピタゴラスが教団のシンボルとして五芒星を採用したことが原因であったように思われる。そうでないと、そもそも五角形の研究を重点的にする必要などないだろう。つまり、まず五芒星が神聖視されて、その結果、五角形の研究が進み、これが黄金三角の発見、さらには黄金分割へと理解と研究が進んだと考えるのが妥当に思われる。
実際、五芒星を重視する理由など本来どこにも無い。今でこそ魔法の象徴である五芒星(五角形)であるが、歴史の当初においてそんなことはなかった。五芒星の使用は古代メソポタミアのシュメール文明にまで遡るが、当時の五芒星は単に領域を示す象形文字であった。例えばシュメール文明における王の称号、ルガル・アン・ウブ・ダ・リンム・バ すなわち”四界の王”。ここで使われるウブが五芒星であり、強いて意訳すると、この時代の五芒星には”天下”程度の意味しかなかった。
かように五芒星は、本来、魔術的な意味を持っていなかった。では、五芒星が魔的な意味を持つようになったのはいつか? 2世紀の作家ルキアノスは、ピタゴラス教団の人々は手紙の冒頭で、あなたに健康を、と挨拶し、五芒星、すなわち”絡み合った三つの三角”を教団のシンボルにしていたと書き残している。絡み合った三角とは黄金三角で五芒星が作られていること、これを人々が理解していたことを示唆するし、五芒星が魔的な意味を持つに至っていたことがわかるだろう。
やはり五芒星を魔術にしたのはピタゴラスであった。そうであるなら、五角形(五芒星と黄金三角)の研究が古代ギリシャで行われたのは、これが原因であったのだろう。つまり三角関数は魔法陣作成術を応用して完成にこぎつけたのであった。
さて、魔法陣作成術と言ったが、この言い様はやや拡大解釈でもある。ピタゴラス教団はシンボルとして五芒星を用いただけで、五芒星で悪魔を呼び出すとか封じ込めるとか、そういうことをしたわけではないので。とはいえ、インチキ教団のシンボルとして神聖視された図形を研究するとは、広い意味で言うと魔法陣研究ではある。
ちなみに、かような次第で魔術とからみあったがため、五芒星は都市伝説が多い。今回の漫画を描くにあたって一応調べたが、ちまたに流布している話のほとんどはデマや拡大解釈、創作、嘘っぱちであった。特に2003年に出版された推理小説「ダ・ヴィンチ・コード」に由来する創作が非常に多かった。
古代文明では五芒星が女神のシンボルとされた。これは嘘である。そして多分、15世紀の作家アグリッパの書いた魔術本の記述を拡大解釈したものと思われる。そしてそもそもアグリッパの記述が勘違いであった。彼は五芒星はヒュギエイア女神のシンボルと書いた。これはピタゴラス教団の人々が健康(ヒュギエイア)と述べたことと、教団のシンボルが五芒星であることを混同したものに思われる。
ピタゴラスは五芒星に五大元素を配置した。この俗説も嘘で、こちらは多分、アグリッパの魔術書に書かれた内容を拡大解釈したものだろう。
メソポタミアでは五惑星が五芒星に配置された。これも根強い俗説だが、そのような事実はない。信じる人にお尋ねしたいが、このような記述がされた粘土板をあなたご存知だろうか? 私が調べた限りそんなものはない。
古代メソポタミアでは8年間に金星が地球と5回会合し、五芒星を描くことが知られていた。だから五芒星は金星の女神イシュタルのシンボルになった。これは後半3分の2が嘘。たしかに古バビロニアのアンミサドカ王(Ammisaduqa:アンミサドゥカ)の時代に金星の会合が記録されており、それが粘土板として出土している。いわゆる金星文書だが、しかしそれだけであるし、イシュタルのシンボルはそもそも八芒星だ。
こうした五芒星に関する噂の多くは「ダ・ヴィンチ・コード」が由来であった。作り話でしかない小説の記述を本当だと思い込んで鵜呑みにする人がこれほど多いとは驚きである。もちろん、魔法とはこういうものではあった。たわいない俗説と嘘から出来上がったもの、それが魔法だ。だがしかし、それでもなお、創作にすぎないものを無批判に信じて流布させる。これは端から見ていて感心しない。たとえそれが魔法という、敗残者の理論の本質であったとしてもだ。
付録
先に述べたようにネットに存在する俗説、古代メソポタミアでは金星が五芒星を描くので、五芒星が金星の女神イシュタルの象徴にされたという話。これはまったくの作り話である。ただし金星が8年間に5回地球と最接近(会合)するので星形を描く、というのは本当であった。紀元後2世紀、ローマ帝国統治下のギリシャ人、プトレマイオスは二つの円運動を組み合わせることで金星の動きを説明したが、それを図解すると以下のようになる。

現代人が以上の模様を見た時、美しいと言う人もいれば、天動説は無駄に複雑〜ww と馬鹿にした態度を取る人もいる。しかし地球から見た金星の動きとは、動く金星を動く地球から見たものであって、要するに地球軌道と金星軌道の合成であった。プトレマイオスが採用した二つの円運動の組み合わせとは、金星軌道と地球軌道の合成に他ならず、実際、私たちから見ると確かに金星はこのように動くのである(要するにプトレマイオスの天動説を馬鹿にする人はそもそも星の運行をちゃんと見たことがないのだ。複雑もなにも本当に惑星はこう動くのだから)。
さて、以上に掲げた二つの円運動から、金星の動きを強調すると以下のようになる。

かようにハート型をした動線が得られるが、これは金星が地球に一番近づき、そこから離れて、さらにもう一度地球に近づくまでの一巡を示している。二つの惑星が出会い会合して離れ、次に会合するまでの一巡。これを会合周期という。そして以上の動線は会合周期における金星の軌道であった(正確に言うと地球から見た会合周期一巡における金星の動きである)。
さて、地球はこの図の中心にあり、ハートの窪んだ部分が地球のあるべき中心に一番近づいている。つまりこここそ、金星が地球に一番近づく場所であり、すなわち会合する場所であった。さて、この会合周期一巡に要する日数は584日。つまり1年と219日。もし金星と地球が一番近づく(会合する)周期がきっかり1年365日であったのなら、金星と地球はいつも同じ場所で出会うだろう。もしそうだったら、地球から見ると金星はいつも同じ星座で地球に一番近づくのである。しかしそうではない。だから金星が地球に一番近づく星座は出会いの年ごとにずれていく。
一方、この一巡の日数584日とは、5倍すれば2920日であり、この日数は365日の8倍に等しい。つまり金星は地球と5回会合すると、8年前と同じ場所にやってくる。つまりは同じ星座に戻ってくる。戻ってくるとは会合が天空を一周したということ。戻ってきた時が5回目の会合。だから地球を中心にして金星の動きを8年分重ねて5回の会合場所をつなげると、それは五芒星になるのであった。

かように、金星の最接近を描くと五芒星になるという知識は正しい。しかし、だからメソポタミアの人々が五芒星を金星の女神イシュタルの象徴としたという話は嘘だ。なぜなら、二つの円運動で金星の動きを説明する。このような、幾何学で運動を説明するという発想は古代ギリシャのものだったからである。古代メソポタミアの人々は、運動は方程式で解き、幾何学では考えなかった。だから古代メソポタミアの人々が金星の運行を五芒星で理解したということはありえない。そもそもメソポタミアの人々がイシュタル女神を星で示す場合、それは五芒星ではなく八芒星である。
参考文献
アルマゲスト 恒星社
世界の名著9 ギリシャの科学 エウクレイデス 原論
ギリシャ数学史 T.L.ヒース 共立出版
古代の数学 A.アーボー 河出書房
[A Mathematical History of the Golden Number] Roger Herz-Fischler pp65