Log Log 尺のなぞ(計算尺研究)
謝辞：以下の「研究」は Yahoo groups slide rule mailing list で Dave Martindale, Ted Stern, Duane Croft, Fritz その他の方々に教えて頂きました。
LL尺は 2.341.56 のようなべき乗を計算する為の尺です。原理はべき乗 Xa は２回log を取ると log(a) + log(log(X)) となり、足し算で計算出来る、と言う事を利用しています。
例えば下の図は年利 1.5% の複利の利率を計算している所で、C尺の左端を LL1 尺の 1.015 に合わせています。これでカーソルを C尺の任意のところへ合わせて LL尺を読み取ると利率が出ます。例では２年目の利率 3.02% を示しています。同じ利率で 12 年目の場合は C尺の 1.2 の下の LL2尺で 19.6% と読めます。
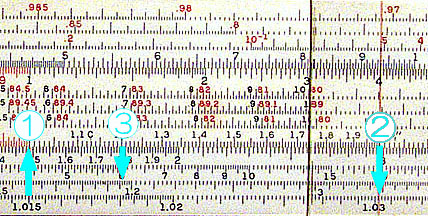
図１ 利率1.5%で２年目と１２年目の利子は？(Ricoh 151)
所で LL尺の左端には 1.1 とか 1.01 とかが有りますが、ぴったりＤ尺の 1.0 の上ではありません。log(log(1.1)) を計算すると、-1.383076 となり、(<-関数電卓で：違反かな？これ ;-) これは -2 + 0.616924 で、仮数は 0ではありません。普通に考えると、0.62 は尺の中央より右です。なのに 1.1 は D尺の左端にあります。これはどうしてでしょうか？
スケールを良く見ると、LL0 の 1.001 がぴったりの位置に有りますし、LL3 の上で自然数 e が丁度Ｄ尺の 1.0 のところに有ります。でもこの二つの数は同じではなく、log(log(1.001) = -4+0.63756725 ですし、log(log(e)) = -1+0.63778431 で、両者の仮数は 0.03% 違うのです。
ここで２つの疑問が生じます。一つはどうして仮数が 0.6 なのに原点に近い所に置いてあるのでしょうか？ 二つ目の疑問は 1.001 と e と、どちらが正解でしょうか？ と言う事です。
最初の問題は比較的簡単で、直裁的には log-log の数値そのままの所へ目盛を刻めば良いと思うのですが、（実際、C、D 等の普通の尺ではそうなっていますね。）log-log尺の場合、計算は C尺上の長さを使うのみで、答えは LL尺で読み取ります。つまり LL尺は LL尺同士の相互関係が保たれる限り、どこに「原点」を置いても良いのです。ですから、なにか別の条件を付けて原点を選べば良いのです。
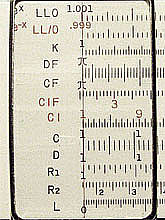
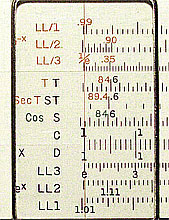
図２ LL尺の原点付近 (Post 1460)
そこで第二の疑問点ですが、これは先輩に聞いて判りました。
大多数の計算尺では LL 尺の基準点は自然数 "e" に取ってある、と言うのです。それを別の見方をすると、最初のログは natural log (ln) で次のログは10進のログを取る、ということになります。そうすると Log10(ln(e)) = 0.0 になり、仮数は始めから 0 となり、悩まなくても良くなります。更にこうすると自然対数の値 ln(x) を D尺で読み取ることが出来るのです。 これは特許ですね、きっと。(^^)
更にびっくりする事は、e をベースに取る事によって 1.01, 1.001, 1.0001 等が皆原点（の近く）に来る、と言うことです。10進で考える我々には都合の良い結果ですね。
「これは都合の良い偶然ですね。」と私が言ったら、先輩が「いや、これは当然なのだ。なぜなら、テーラー展開の第２項まで取ると ex ≒ 1 + x だからだ。」と言います。
なになに、それだけでは判らないよ。では X = .001 としてこの式の両辺を自然対数を取ると、0.001 ≒ ln(1.001)、もう一回 log10 を取ると -3.0 ≒ log(ln(1.001)) となり、確かに左辺の仮数は０ですから、log(ln(1.001)) は原点近くに来ると言えます。x が 10-n (nは０を含む正の整数)であればいつも左辺は -n.0、となるので原点に限りなく近いところに有りますね。う〜む、「当然」と言えるかな、と納得しました。
１０インチの計算尺には LL 尺がついている時は LL0, LL1, LL2, LL3 と、その逆数の合計８本の LL 尺が付いています。所が５インチの計算尺には LL0 尺が付いていないことが多いのです。そんな時 0.3% の利率の複利で12年では？とか聞かれたらどうしましょうか？LL1 尺では 1.01 以下、つまり 1% 以下の目盛がありません。
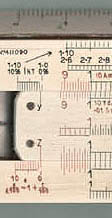
それにはＤ尺を代用に使えば良いのです。Ｄ尺の左端の 1.0 を 1.001 と読み替えて使います。図３の様に Ｄ尺の 3.0 を 1.003 と読み替え、滑尺の左端をここに合わせます。そしてＣ尺の 1.2 にカーソルを合わせ 12年で桁が上がりますから、LL1 を読みます。答えは 1.0366 と読み取れます。
この方法はかなり精度が良く、精度の一番悪くなるスケールの右端でスケールの全長に対して 0.2% の誤差しか有りません。
図３ Ｄ尺を LL0 尺の代用に(Pickett N600-ES)
どうしてこうなるんだ？と言う疑問に先輩は「x が 0 に近い時は ex ≒ 1 + x だからだよ。」と言います。
これは先に出てきた式ですが、両辺を自然対数と10進対数を取ると；
log10x ≒ log10ln(1+x)
となります。左辺の仮数は D 尺になりますから、確かに右辺の近似値は D 尺である、と言えます。
ですから LL0 尺のもっと下、1.0001 と言うレンジも D 尺で代用できます。もっとも、こんな値だと、 (1+x)n ≒ 1 + nx の方が簡単ですが。(笑)
あります。これも先輩に教わったのですが、D 尺へいきなり X を置くのでは無く、x(1-x/2) を計算してそれを D 尺に置きます。(1-x/2)
はいわば補正項ですね。例えば 1.01 の場合は x=0.01 ですから補正項を入れて計算すると 0.00995 となります。
例えば 0.7% の複利計算の場合は、 D 尺の 7.0 の所へ C 尺の右端を持って来て、カーソルを C尺の 9.95 にあわせればD尺上により正確な
LL0(1.007) の値を求めることが出来ます。
ここまですると精度は格段に上がって 1.01 の所、つまり D 尺の右端で 0.001% の誤差しか有りません。
所でこの補正量は５吋尺では最大の右端で 0.25mm です。そしてこの補正量は尺の左側に見えています。LL1 尺の左端と D 尺の 1.0
との差がそうです。微小な補正なので目で最大の補正量を確認しながら滑尺を「ちょっと押してやる」程度で出来るのでは？
いかげん？ 元々アナログだからいいんじゃないの？
この方法の数学的な根拠は次の通りです。まず、自然対数 ln(x) のテーラー展開を考えます。
ln(a+x) = ln(a) + x/a - x2/2a2 + x3/3a3 ...
a = 1 と置いて第二項まで取って書きかえると；
ln(1+x) ≒ x - x2/2 = x(1-x/2)
が得られます。この式の両辺の常用対数を取ると左辺は求めたい LL 尺の位置、右辺は補正を加えた D 尺の長さになっています。
昔の「電気尺 (Electrical)」だと LL2 と LL3 しか無いですね。これだと複利計算は 10% 以上の利率しか計算できません。でも皆さんが英国 Thornton 社の計算尺で「ログログ差分 (Log Log Differential) 尺」付きを持っていれば計算来ます。このスケールは Thornton 社の特許だそうで、計算尺の左端にちょこんとある短いスケールです。Ｄ尺を LL1 尺に代用するときの補正に使います。
上の「ＬＬ尺のなぞ３」で LL0 尺の代わりのＤ尺の話題が有りましたが、これはもう一つ上の LL1 尺をＤ尺で代用しようと言うものです。
例えば年利２％で16年預けた時の複利の利率の計算は：
・最初に差分尺の２％のところに滑尺上の y を合わせ、Ｃ尺の 2.0 へカーソルを合わせます。これでＤ尺へ補正済のＬＬ１の値が取れました。
・滑尺を移動させてカーソル位置に C尺の端 (1.0 又は 10.0) をあわせます。
・Ｃ尺の 1.6 へカーソルを移動し、LL2 尺の値 1.37 を得ます。
現在の計算尺は 17世紀に William Oughtred という僧侶によって発明されました。これに先立って Edmund Gunter によってログ尺が発明されましたが、この尺は一本で、デバイダーを使って寸法を移しながら掛け算、割り算を行う物でした。それを Oughtred は２本のログ尺を使って互いに滑らせることで計算をはるかに簡単に出来る様に改良したのです。（円形の計算尺だったと言う記述もあります）
この人の名前をとった計算尺の収集家のための協会 Oughtred Society が有ります。この協会へ入会すれば年２回の、計算尺に関する色々な情報が満載の会報が配られます。また協会の年次総会が米国とヨーロッパで開かれ、その時にはデモや、オークションが行われるとの事です。
LL尺はその実現法にはメーカ毎にかなり違っていて、それぞれ面白い工夫もされています。それぞれのメーカーの違いを見て見ましょう。
| メーカー | 名称、特徴 | 例 |
|---|---|---|
| Faber Castell | LL0, LL1, .. , 逆数は LL00, LL01, .. と命名されています。 同社の 2/83N Nobo Biplex の LL0 尺は D尺と共用になっていて、右半分の D尺には例えば 1.0 10 05 と書かれています。これは D尺の 10 の所は正確には 1.01 では無く、1.0105 だよ、といっているのです。 |
2/83N 63/83 |
| Hemmi | LL0, LL1, .., 逆数は LL/0, LL/1 .. と表記されています。一部の尺では逆数が LL00 - LL03.. と表示されたのもあります。 | 259D P261 |
| K&E | 同社の場合は少なくとも３通りの表記があり、時代とともに変遷した形跡があります。もっとも新しい 68-1100 Deci-Lon の場合は Ln0 - Ln3, 逆数は Ln-0 - Ln-3、N4081-3 の場合 LL1 - LL3, 逆数は LL01 - LL03、そして比較的古い 4080-3 の場合は LL1 - LL3, 逆数は LL0, LL00 です。最後の場合は変則的で、LL1 に対応するのが LL0 で、LL2 に対応するのが LL00 です。 | 68-1100 N4081-3 4080-3 |
Pickett | 同社の LL尺は "Dual Base" と呼ばれ、横線の上下に正方向の目盛りと逆数の目盛りが対で目盛られています。逆数を一目で見つけることが出来る特徴と、縦方向のスペースを節約して多くのスケールを乗せる工夫です。その他にも、LL1 - LL3 と、逆数が LL0, LL00 の尺も有ります。 | N803ES 500T |
| Post | Post 社は Hemmi と同じ、LL0 - LL3, 逆数が LL/0 - LL/3 の形式を使っています。他に、LL1 - LL3, 逆数が LL0, LL00 の形式もあります。 | 1460 1462H |
| Ricoh | Ricoh 社の場合は LL1 - LL3, 逆数は LL1- - LL3- という表示を用いています。（上のバーは実際には数字の上に書いてあります。） | 151 |