 図1
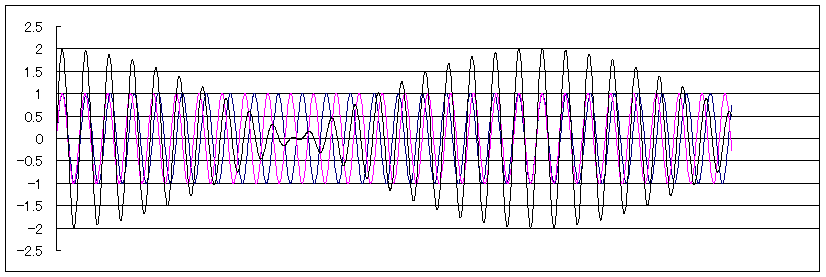
図1周波数とうなり現象について
周波数440Hzの音波は「ラ」の高さの音になります。これを三角関数で表すと、y=sin440x となりますね。
これに対して、周波数を440Hzから少しだけ変えた音波を作ります。例えば450Hzだとすると、y=sin450x
となりますね。さて、これらのグラフを描くと下のようになります。ピンクがy=sin440x 青がy=sin450xの
グラフです。これを見ると、最初はほとんど同じグラフなのですが、だんだん位相がずれていきます。
下のグラフの中央付近ではほとんど逆位相になる所もあります。
さて、これら2つのグラフを合成すると、どうなるでしょう。図の黒いグラフが合成したグラフです。同位相
のところでは、振幅が大きくなりますので、音が強くなります。また、逆位相のところでは振幅は0に近づく
ので、音は弱くなります。(図2の拡大図参照)
このような現象が、周期的に繰り返しますので、グラフを遠くからみると、図3のようになります。
これは、音が強くなったり弱くなったりが周期的に繰り返される、「うなり」という現象ですね。
これを利用して電話のコール音(サンプルは800Hzと820Hz)なども作れるわけです。
上のアンダーライン上をクリックすると音が聞こえます
このように自分で作ったサインカーブの音を聴いたり、合成した関数の音を聞いたり、また、それを加工
したりできる便利なソフトを、本校の物理の先生である村上弘さんがエクセルで開発されました。通常の
wavファイルも数値化データとして読み込んで加工できるスグレモノです。気になる方はメールください。
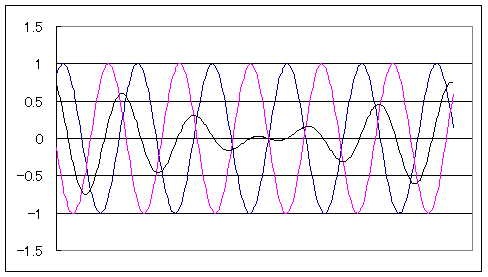 図2(逆位相になる部分・合成関数の振幅は小さくなる)
図2(逆位相になる部分・合成関数の振幅は小さくなる)
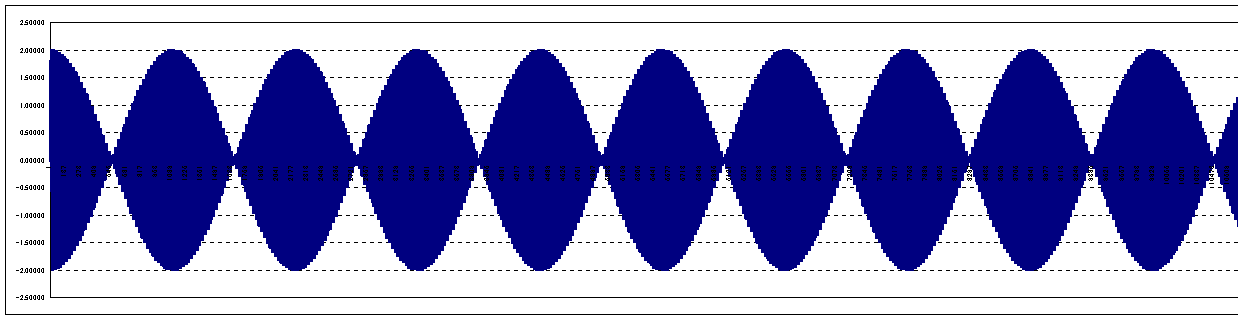
図3(10000位までの範囲でグラフを見る)
さて、周波数と弦の長さには、次のような関係式がありました。

つまり、周波数(振動数)と弦の長さは反比例しているのですね。
下表は、弦の長さを、全体の分数比で表してドレミファソラシドを作る「純正律」の音階と、ドから半音ずつ、2の12乗根(約1.059)
をかけていくことによって音階を作る平均率について、振動数の値を比較してみました。僅かですが、振動数に差があることが
わかりますね。ですから、純正律で調律された楽器と平均率で調律された楽器を同時に同じ音程を演奏すれば、うなりが生ずる
わけです。このうなりまで計算にいれて作曲する人もいると聞きましたが本当かどうかわかりません。
| 純正律・弦の長さの比 | 純正律・振動数の比 | 平均率・振動数の比 |
振動数の差 |
|
| ド | 1 | 1 | 1 |
0 |
| レ | 8/9 | 9/8=1.125 | 1.122462048 | -0.002537952 |
| ミ | 4/5 | 5/4=1.25 |
1.25992105 |
0.00992105 |
| ファ | 3/4 | 4/3=1.333 | 1.334839854 | 0.001506521 |
| ソ | 2/3 | 3/2=1.5 | 1.498307077 | -0.001692923 |
| ラ | 3/5 | 5/3=1.666 | 1.681792831 | 0.015126164 |
| シ | 8/15 | 15/8=1.875 | 1.887748625 | 0.012748625 |
| ド | 1/2 | 2 | 2 | 0 |