杜陵サークル3月例会から <戻る> ![]()
3月3日に岩手大学小宮山研究室で行われた杜陵サークルの話題を
紹介します。杜陵サークルのホームページは着々と(?)作成中であり
ます。そのうち大々的にオープンすることと思います。ご期待ください。
伊藤潤一1 ┃下河原A ┃伊藤潤一2 ┃しもまっち┃ 小宮山先生
伊藤先生のコマーシャル 戻る
 |
まずはネコ仙人の産みの親、伊藤先生からのコマーシャル。
大好評だった「微分・積分の意味がわかる」(ベレ出版/野崎昭弘・何森仁・伊藤潤一・小沢健一共著)に引き続き、「数と計算がわかる」(同上)が出版されました。いろいろな数、計算のしくみが1ページ1話題で楽しく解説されています。小学生から大学生、大人も楽しめるオススメの本です。税込み1400円。 欲しい方は書店でお求め下さい。直接本人にメールでもいいと思いますよ。 |
下河原・A先生の発表より 戻る
| 若手のホープの下河原・A氏は、2次曲線上の3点によってできる三角形の面積について発表を行いました。右写真は、楕円上の3点によってできる三角形の面積の公式を定式化したときに、「それではその公式から、面積が最大となるのはどういう状態のときか」などとちゃちゃを入れる人がいて(私です)、A氏がそれを受けて偏微分しているところです。なお、このレポートの内容は「初等数学」(松田康雄編)に3回にわたって連載される予定です。 |  |
| 内容は豊富なのですが、サークルでは次のことが話題となりました。ごくごく簡単に紹介しましょう。
その1【3点が与えられたときの三角形の面積】 A(x1,y1),B(x2,y2),C(x3,y3) とすると、ベクトルの方法で、三角形の面積は次のようになる。 S={x1(y2-y3)+x2(y3-y1)+x3(y1-y2)}/2 |
その3【双曲線上に3点がある場合】
双曲線上の3点を、 A(a/cosα,btanα),B(a/cosβ,btanβ),C(a/cosγ,btanγ) と置いて、楕円と同じ計算をしていきます。すると、 S=(ab/2)│{sin(α-β)/2 sin(β-γ)/2 sin(γ-α)/2} /(cosα cosβ cosγ)│ という式が得られた。 |
| その2【楕円上に3点がある場合】
その1で求めた公式に、楕円上の点をA(acosα,bsinα),B(acosβ,bsinβ),C(acosγ,bsinγ)として代入して整理すれば楕円上の3点を結んでできる三角形の面積が求まる。加法定理や和積公式などを駆使して、 S=2ab│sin(α-β)/2 ・sin(β-γ)/2 ・sin(γ-α)/2│というきれいな式を得た。
|
その4【双曲線関数を使って】
その3において、双曲線上の3点を、双曲線関数を用いて(acoshα,bsinhα),B(acoshβ,bsinhβ), C(acoshγ,bsinhγ)と表せば、双曲線関数においても三角関数と同様の加法定理が成り立つことから、 S=2ab│sinh(α-β)/2 ・sinh(β-γ)/2 ・sinh(γ-α)/2│ という、その2において、三角関数を双曲線関数に置き換えたものが得られる。 |
 |
ちょっときどった下河原・A氏(右)、左は小倉ちゃん。小倉先生の趣味は絵画です。今度サークルで皆で絵を描こうという話が持ち上がっています。 |
伊藤先生の発表レポートより 戻る
 |
伊藤潤一先生は、「個数の処理」授業メモという話です。平舘高校で行った「個数の処理」の授業を終えて、そのまとめを行ったというもの。なんでもこのレポートは、きれいにノートをとっている何人かの生徒からノートを借りまくって作ったものだそうです。
以下に、そのレポートから一部を紹介させていただきます。 |
| 【集合】
『集合とはものの集まりである』。「もの」とは何だろうか。これは集合論のゲオルク・カントールの言っているように「直感または思惟の対象となるものです。ということは、{鉛筆、消しゴム、ノート}の文房具セットのように直接見たりさわったりするものも集合になるし、{ゴジラ、ガメラ、モスラ・・・}の怪獣のように頭の中で考えるようなものも集合となるのです。 註 うーん。カントールときたか。格調高いぞ。そのわりに実例が{ゴジラ、ガメラ、モスラ・・・}はかわいいぞ。 【集合の表記】 自然数全体の集合は、{1,2,3,4,・・・}と表されます。さらりと書きましたが、「無限にどこまでも続くものを中括弧{,}でくくることができるだろうか?」という疑問が残ります。なんとなく西遊記の孫悟空とお釈迦様のお話を思い出しませんか。孫悟空がきんと雲で息の続く限り飛び世界の果てに到着したと思われたのに、実はお釈迦様の手の中から出ることができなかったという話です。集合の中括弧は、お釈迦様のような存在で、どんなに自然数が動き回っても掌握してしまうのです。 註 なるほど。{}はお釈迦様の手だったのか・・・なんかうまく騙されているような気もするなあ。
|
【所属記号】
所属記号∈∋について説明します。この独特な記号の由来は諸説あります。単純なのはelementの頭文字eに対するギリシャ文字εから∈に変化したという説です。すこし複雑なのが、「~である」(英語のis)に相当するギリシャ語εσ’ιの頭文字εを取ったという説です。「属する」という意味でなく「である」にしたセンスは面白い。例えば、Mを平方数の集合とすると、 9は平方数である⇔9∈M とパラレルな関係になるのです。所属記号∈を使い始めたのは、記号論理をやっていたペアノであるといわれています。 註 そうだったんですか。わたしゃあ∈は熊手の形なので、集合のボスが熊手で要素をかき集めているんじゃないかと思っていましたよ(冗談) 【全体集合と補集合】 全体集合と補集合は相補的な関係です。補集合を考えるには、全体集合を考えざるを得ないし、全体集合を考えるには、ある部分集合の補集合を考えればいいのです。例えば、バスケ部員でないものの集合を考えるには、どうしても全体集合を設定せざるを得ません。そうでないと、テニス部員や美術部員などの他に、帰宅部員、教職員、お父さんお母さん、兄弟姉妹、祖父祖母、近所の人々、飼っている犬、ネコ、豚、牛、畑のカラス、トンビ、カメ虫、ミミズ、バクテリアそして机、椅子、ノート、シャーペン、自転車、トラクター、家のテレビ、ラジカセ、マンガ、松島奈々子のポスター・・・考えればきりがありません。 全体集合を1年A組36名の生徒にすると、バスケ部員の補集合は簡単にわかりますよ。 註 全体集合と補集合を相補的に考えるのはいいですよね。しかし、なぜ、最後に松島奈々子が出てきたのかナゾだ。伊藤先生は密かに松島奈々子ファンらしい。 |
しもまっちの発表 戻る
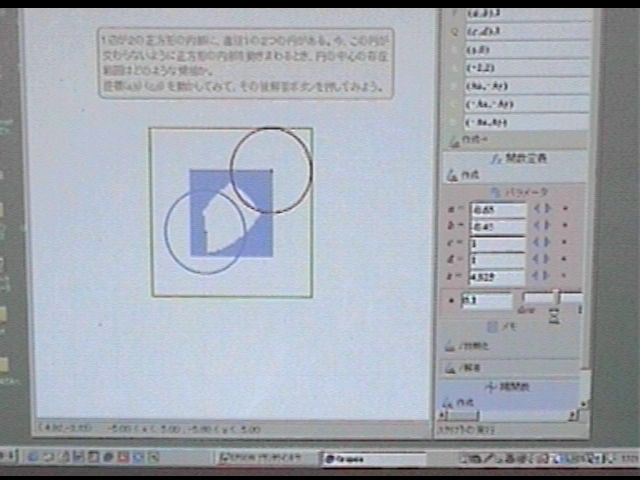 |
しもまっち氏はパソコンとプロジェクタを持っていっていくつかの発表を行いました。 ①正方形内を動く2つの円 : これは左写真のように正方形内をはみ出さずなおかつ2円が互いに交わらないように動いたとき、中心の軌跡はどうなるかという問題。grapesのスクリプトを使って求めました。 ②パラメータ表示された関数の増減とグラフ :dx/dtとdy/dtを成分とするベクトルを表示しながらグラフの動きを見ていこうというもの。これもgrapesでのセッションです。 ③微積分学の基本定理のイメージ : やはりこれもgrapesを用いたものです。グラフ上の点に、dx
とdy(=f'(x)dx)
の動座標軸をつけながら動かして、微積分学の基本定理を図形的に理解しようというものです。SEGなんかの本にあるやつです。 ④The
Amazing KOSUKE's Home Page :小学校4年生のこうすけ君のホームページが凄い!彼のページから、彼の考えたピタゴラス数を求めるうまい方法を紹介しました。
|
小宮山先生 戻る
 |
| 岩手大学の小宮山先生です。小宮山先生なくしてサークルはありません。場所の提供と助言を与えてくれます。 |
おまけのワンショット 戻る
 |
| 新進気鋭の齋藤照美先生。最初彼の名前を聞いて女性と勘違いして、楽しみにしていたサークル員がいたとのこと。彼はベースボールプレイヤーでもあるのです。 |