相似拡大される11種類のピース

　これは、広島の中原さんが発見したものです。私のほうでその話の紹介と、簡単な証明をしてみました。　

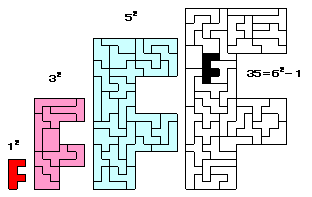
　ヘキソミノは全部で35種類あり、35は、35＝1²+3²+5² と分解できる。このことから、35個の全ピースを使って、あるピースと、辺を3倍に相似拡大（面積は9倍）した図形と、5倍（面積は25倍）に相似拡大した図形とに表すことができる（図の左から３つ参照）。

（一方、35=6²−1　ともできることから、あるピースを6倍に相似拡大した図形を、1個のピースを除いて作ることもできる（図の一番右参照））。

これは、35種類のすべてのピースで可能なことではなく、上図のようなピースの他、全部で11種類のピースでしか作ることはできない。

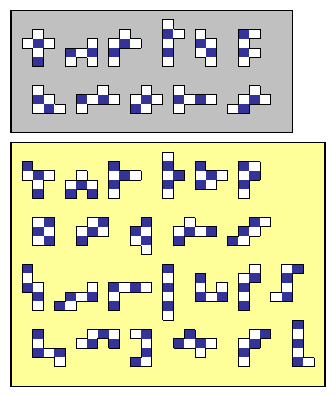
35個の各々のピースを市松模様で塗り分けてパリティチェックすると、上図のように、２−４型のピース11個と、３−３型のピース24個に分かれる。

今、下図のように、３−３型のピースで3倍拡大、5倍拡大の図形を作ったとしよう。このとき、それら２つの図形の白黒の個数は明らかに同数である。

ところが、３−３型のピースは24個で、最初にその1個を使っているから残りは23個である。すると、3倍図形、5倍図形の一方は必ず３−３型のピースは偶数個になってしまう。つまりそこでは、何個かの２−４型のピースと、偶数個の３−３型のピースの組み合わせなので、白も黒もともに偶数個になってしまう。

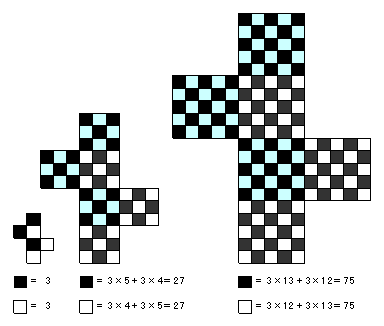　　　へきそみのらんどへ