│Grapesの世界へ│面白数学らんど│音楽&数学らんど│リンク│エクセルで面白数学│ホーム│
あなたもGrapesの世界へ⑭
マンデルブロー集合を描く
|
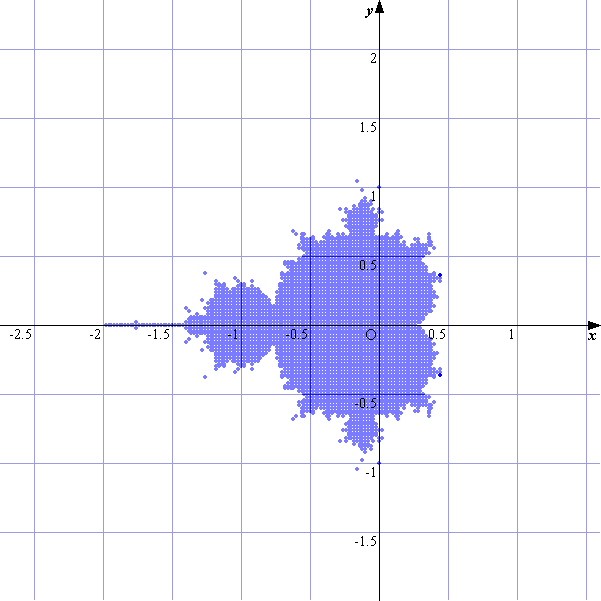
Grapesのスクリプト機能を使ってマンデルブロー集合を描画してみました。ちょっと時間はかかりますが、図のようになんとかマンデルブロー集合らしくなりました。 |
|
|
# //go |
f(Zn+1)=Zn2+C という複素写像を考えます。n→∞としたとき、Znの絶対値が発散しないような複素数Cの集合を考えます。特に、Z0=0であるとき、その集合をマンデルブロー集合といいます。ここでは、Cを実部-2~0.5 、虚部 -1.35~1.35として0.2刻みで複素数を動かして、描画してみました。確か、途中で絶対値が2を越えれば必ず発散するという定理があったと思ったので、とりあえず20項まで計算しても絶対値が2より大きくならないようなCをプロットするというプログラムにしました。かなりアバウトですがイメージはつかめると思います。描画範囲を変えて実行すると、部分拡大などもできます。(時間がちょっとかかります)スクリプトは左です。 基本図形でP(s,t)と、Q(Px,-Py)を作ります。そして、左のテキストをコピーして、Grapesのメモに貼り付ければOKです。描画範囲とstep数を変えればいろいろな部分を描画できます。 |


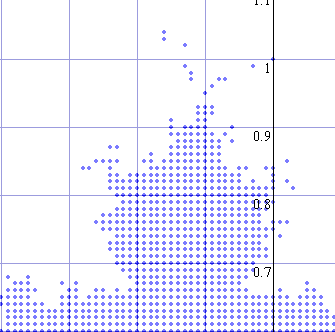
左は全体像。右は、実部-0.6~0.1、虚部0.6~1.3まで(0.01刻み)を拡大描画