パスカルの三角形に潜む母関数　　<<面白数学らんど>>

１　横の列

　　図のように、パスカルの三角形の横の数列は、（１＋ｘ）^ｎのｘ^ｋの各係数になっています。これは高校でも教える内容です。

　例えば、（０段から数えて）４段目は、（１＋ｘ）^４＝１＋４ｘ＋６ｘ^２＋４ｘ^３＋１ｘ^４　ですね。

　このようなとき、（１＋ｘ）^４は、数列［1,4,6,4,1］を生成する母関数（生成関数）といいます。

２　縦の列

　　では、今度は縦の列に注目してみましょう。

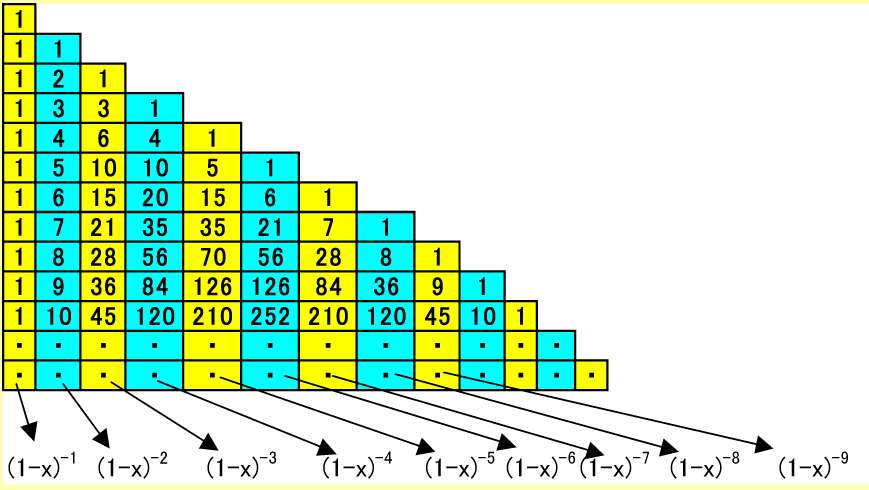
　　縦の列は、（１−ｘ）^-ｎの展開項の係数になっています。例えば、（１−ｘ）^−２＝1+2x+3x²+4x³+5x⁴+…

　　今、ｆ_１＝（１−ｘ）^−１、ｆ_２＝（１−ｘ）^−２とすると、［1,3,6,10,15,…］を表す母関数をf₃とすると、

　　　　　　ｆ_３＝ｆ_２＋ｘｆ_２＋ｘ^２ｆ_２＋ｘ^３ｆ_２＋…＝(1+x+x²+x³+…)ｆ_２＝ｆ_１ｆ_２＝（１−ｘ）^−３

　　　　　　　（1桁ずつずらして足す）　となり、一般にｎ列目の母関数が（１−ｘ）^−ｎ　がわかります。

３　斜めの和

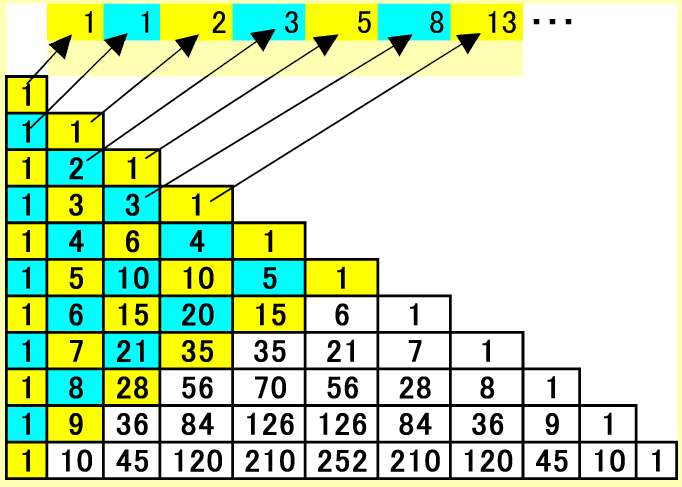
　　パスカルの三角形の各項を図のように斜めに加えるとフィボナッチ数列が現れます。これは結構有名です。

　　フィボナッチ数列の母関数は、２で述べたパスカルの三角形の縦の母関数（１−ｘ）^−ｎを用いて示すことができます。　　　

　　　　　　F=ｆ_１＋ｘ^２ｆ_２＋ｘ^４ｆ_３＋ｘ^６ｆ_４＋…＝1/（１−ｘ−ｘ^２）

４　横の数の平方の和（中央ケイマの数列）

　　最後にちょっと変わったものを紹介します。

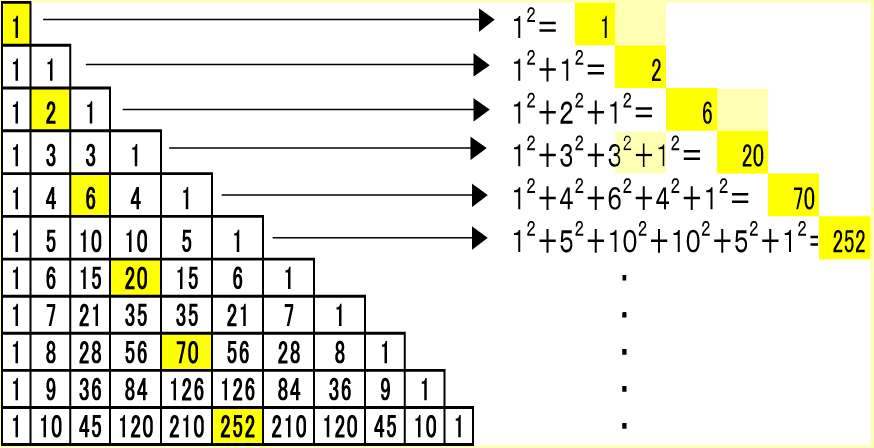
　　図左の、ケイマにとった数列、1,2,6,20,70,252,…はどんな数列でしょう。

　　実は，図右のように、各段の項の平方の和に対応しています。

　　証明は（１＋ｘ）^ｎ（１＋ｘ）^ｎ＝（１＋ｘ）^２ｎ　の両辺のｘ^ｎの係数を比較すれば簡単にできます。