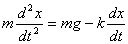
第4章 雨滴の落下速度
水滴には、鉛直下向きに重力、上向きに空気の粘性による抵抗力がはたらく。
水滴が小さいとき、抵抗力の大きさは水滴の速度に比例する。
鉛直下向きにx軸をとり、落下している間の質量変化を無視するとNewtonの運動方程式は、
v=dx/dtを用いて式を整理すると、
これを初期条件t=0でv=0のもとで解くと、
充分時間が経つと、重力と抵抗力がつり合って、
となる。これを水滴の終端速度と呼ぶ。
空気の分子粘性係数をμ、水滴の半径をrとするとStokesの抵抗法則より、
k=6πμr
また、 ρ=103 kg/m-3,g=9.8 m/s2,μ=1.8×10-5 N・sec/m2(15 ℃)より、
よって、終端速度は水滴の半径の2乗に比例する。
この議論が適用できる範囲は、Re<1、すなわちr<0.1mmの範囲である。
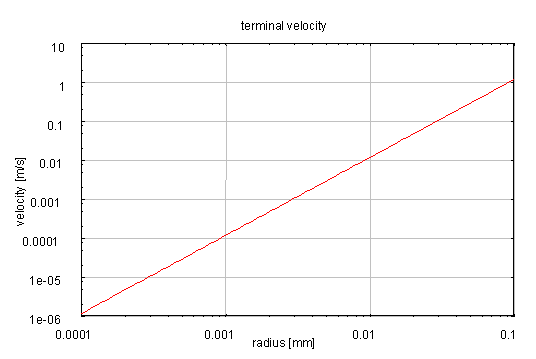
図1:速度に比例する抵抗力がはたらく場合の終端速度
次に、水滴が大きいときを考える。このとき、抵抗力の大きさは水滴の速度の2乗に比例するから、 Newtonの運動方程式は、
v=dx/dtを用いて式を整理すると、
これを初期条件t=0でv=0のもとで解くと、
終端速度は、
空気の分子粘性係数をμ、動粘性係数をν、水滴の半径をrとすると、
k=0.235μπr2/ν
ν=0.15×10-4 m2/sec(15℃)より、
よって、終端速度は水滴の半径の平方根に比例する。
この議論が適用できる範囲は、5×102<Re<2×105、すなわち0.7mm<r<30mmの範囲である。
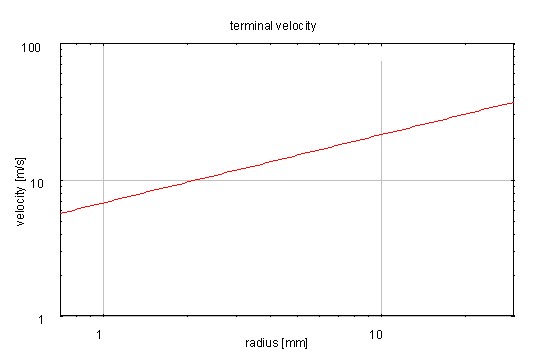
図2:速度の2乗に比例する抵抗力がはたらく場合の終端速度
以上の考察より、いくつかの値を計算してみると、次のような結果が得られた。
半径(mm) 落下速度(cm/sec) 雲粒 0.001 0.012 霧雨粒 0.01 1.2 霧と雨の境 0.1 120 雨粒 0.8 608 〃 1.0 680 〃 2.0 962