◎配列変数・応用編◎　2004.8.15更新

では、今回は配列変数の応用編です。 前回の基礎編でご紹介いたしました「パネルがウガァ！」を題材にしたいと思います。
LiveNovelでプロジェクトファイルを開いて、読み進めてください。

※お詫び：
前コーナーでダウンロードできます「パネルがウガァ！」に、バグがありました。
8月16日に機能を追加しました最新版をアップしましたので、以前のバージョンをお使いの方は改めてダウンロードしてください。
それにともない、このコーナーの解説と異なる画像・計算式などがありますが、基本的に同じものなので問題なく解説を読むことができます。
ご迷惑をおかけしまして、申し訳ありません。
※バグの詳細について：
ゲーム終了後の、次のゲームのレベル選択を行うさい、配列変数「ボード[0-24]」の初期化がされていませんでした。
このため、続けてゲームを行うと、前回の残りパネルが残ってしまい、解けないパターンができてしまいました。

※パネルがウガァ！実行画面


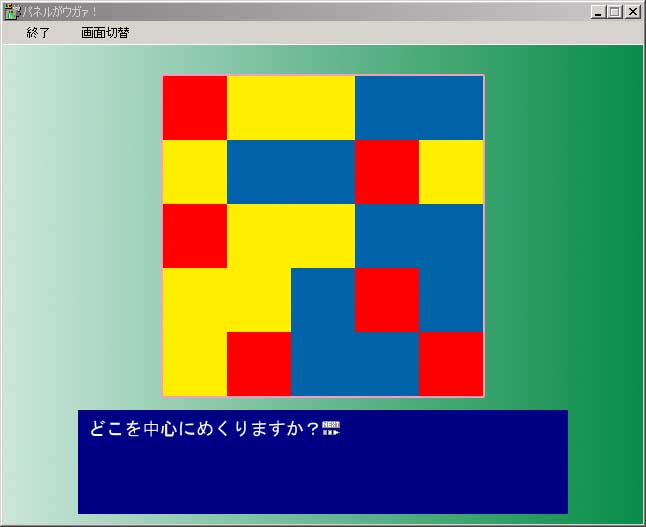
何度見ても面白みもな……いえ、シンプルな画面ですが、まず注目していただきたいのは、ゲームのメイン画面が５×５ブロックに分かれているという点です。
これを見て、「あ、これは二次元配列（５×５）で管理しているな！」と直感できましたら基礎はバッチリです。
ですが、実は二次元配列ではありません。


☆画面は見せかけ
目に映る画像というものは、形さえ整っていれば中身がどう処理されていようと、よほどでなければ問題ありません。
この場合はそれにあてはまり、二次元配列で処理しているように見えて、実は一次元配列です。
これは「どっちが正しい」という話ではなくて、製作者が「どっちが作りやすいか」で決まる問題でしょう。
わたしの場合、たまたま一次元でやるほうを選択しただけでして、初心者のかたはむしろ二次元で作るほうがわかりやすいと思います。


☆製作準備
LiveMakerでゲームを作る場合、まず避けられないのが変数の登録です。
チャートリストなどもあわせて見てください。

※変数リスト


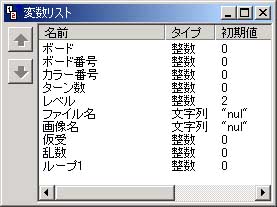
※チャートリスト


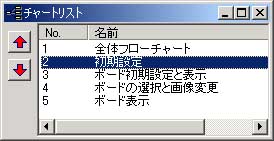
※チャート-全体フローチャート


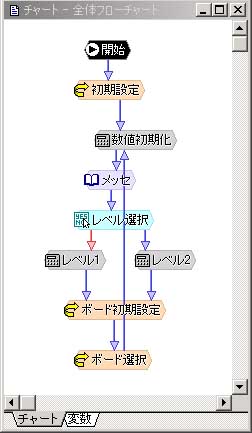
整数変数「ボード」が、今回のキモである配列変数です。
初期設定で配列宣言をしています。

※チャート-初期設定


※計算-配列宣言


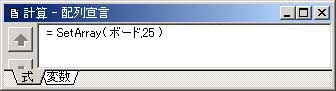
５×５ブロックなので、25の箱を必要とします。
ここで注意していただきたいのは、番号は0から始まるということです。
ですので、25個の箱がありましたら、番号は0〜24となります。

整数変数「ボード番号」は、配列変数「ボード[n]」の「n」の部分、つまり添字を指定するための変数です。
この数値が0〜24以外になると、配列変数の許容範囲を越えてエラーになります。
その性質を利用して、判定に使用していたりします。

整数変数「カラー番号」はパネルの色を記憶する変数で、0は青、1は黄色、2は赤と設定しています。


☆配列変数「ボード」について
ゲーム画面の左上が、配列変数「ボード」の0番となっています。右に行って1、2、3、4、そして上から2段目の左端から5,6,7……と、設定しています。
肝心の中身は、「カラー番号」が入っています。
たとえば、上記のゲーム画面、左上のパネルは赤になっていますね？
これをLiveMakerは「ボード[0]=2」と記憶しているのです。
ではここで問題です。
上から2段目の、右から1番目は、どのように記憶されているでしょうか？

　答え：ボード[9]=1

わかりましたか？
もう一つ、問題を出してみましょう。
整数変数「ボード番号」には、「22」が入っています。
上のゲーム画面では、何色で、カラー番号はいくつでしょうか？

　答え：色は「青」、カラー番号は「0」

これを＜計算＞ノードで使える計算式で書いてみましょう。

　カラー番号　＝　ボード[ボード番号]

と、なります。
このように、添字をわたすだけで答えを得られるのが、配列変数の強みです。
また、繰り返し処理などをするときも添字の数値を換えるだけですむので、プログラムの長さと複雑さを抑える働きがあります。


☆ボードの初期設定
まずはチャートをご覧ください。

※チャート-ボード初期設定と表示


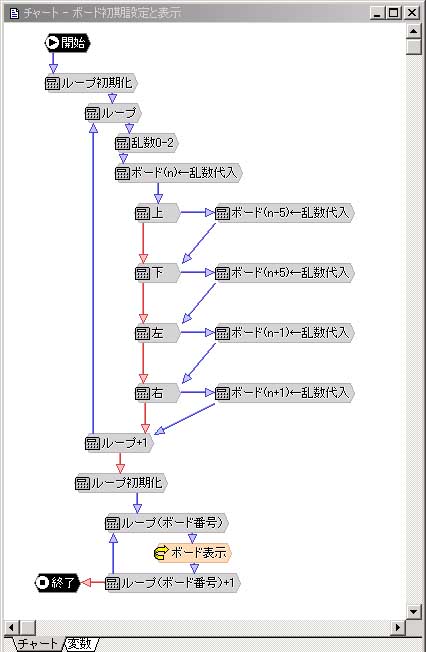
大きく二つのループ作業がありますが、下のループ作業は設定したカラー番号に応じてパネルを表示しているだけなので、解説は省きます。
上部のループでは、20回ほど0〜24の乱数を発生させ、それをボード番号として扱い、対応するボードの色を変化させています。
具体的に申しますと、たとえばゲームレベル２（赤・青・黄の三色モード）で乱数が14だったとします。
ボード[14]に格納されているカラー番号を+1して、それを「３」で割り、「余り」を再びボード[14]にしまっているのです。

Ｑ：「なぜ３で割ったり、余りを代入するの？」

実際に計算をしてみましょう。
ボード[14]の中身が「0（青）」とします。
これを+1して、中身が「1（黄色）」になりました。
次にその「1」を「3」で割ると、答えは0で、余りが1になります。
中身は「1」のままですね。
では今度は中身が「2（赤）」としましょう。
+1して「3」。「3」は色を設定していませんので、このままではエラーになってしまいます。
そこで「3」で割ると、答えは１で、余りは「0」です。
この余りの「0（青）」がボード[14]に入ることなります。
つまり、3で割った余りは「0-1-2-0-1-2-0-1-2……」と繰り返すことになるのです。

さて、次に乱数で選ばれたパネルの上下左右にあたるパネルも変化させておかねばなりません。
これをおこたると、解くことのできないパターンができてしまうかも知れないからです。
なので、上下左右のパネルのカラーも「+1して3で割った『余り』」を代入しておきます。
けれどここで問題が起きます。
外側に面するパネルには、上下左右のいずれかが存在しない場合があります。
これを判定するのが、＜計算＞ノードの「上」〜「右」にあたる一連の処理です。

◎「上にパネルはあるか？」
先ほどの例題と同様、ボード[14]の場合を見てみましょう。
ボード[14]の上のパネルというと、ボード[9]になります。
つまり、もとのボードから-5をした場所が上のパネルになるわけです。
ここで、パネルは全部で25枚、0〜24の数値で表されていることを思い出してください。
もとのパネルから-5をした結果が、0より小さくなるようであれば、そこにパネルはないということになります。
＜上＞ノードの条件がまさにこれで、「-5した結果が0より小さければ、パネルはないので次の判定に飛びなさい」となっています。
もしパネルがあるようなら、カラーを変更してから次の判定に飛ぶようになっています。

◎「下にパネルはあるか？」
これは「上」のときとは逆で、+5した結果がボード番号の範囲外、「24」より大きい場合はパネルがないということになります。
その他については、上記と同様です。

◎「左にパネルはあるか？」
横の場合は「上」や「下」のように「-1」や「+1」をしても、パネルの有無判定はできません。
二次元配列であれば、それで有無がわかるのですが、一次元配列ではすべてがつながっているために判断できないのです。
ではどうしているのかというと、乱数で選ばれたボードを「5」で割り、その「余り」を求めています。
これも計算していただければわかりますが、縦軸にかかわらず、横軸の場所がこれで求められるのです。
「余り」が「0」のとき、指定されたパネルは一番左になります。
一番左ですから、これ以上の左パネルは存在しないことになりますね。
条件「５で割った余りが0のとき、左パネルは存在しない」ので次の処理に移りなさい、ということが＜左＞ノードで行われています。

◎「右にパネルはあるか？」
「左」のときと同じ処理をしています。
こちらは「余り」が「4」かどうかで判定されているだけです。

ワンポイント：「余りを求めるには？」
除算の「余り」だけを計算する「演算子」というものがあります。
「%」がそれで、計算を実行すると、左辺の変数に「余り」が代入されます。
「演算子」については、LiveMakerのヘルプにも出ているので、参考にしてください。


☆パネルの選択と画像の変更
こちらもまずはチャートをご覧ください。

※チャート-ボードの選択と画像変更


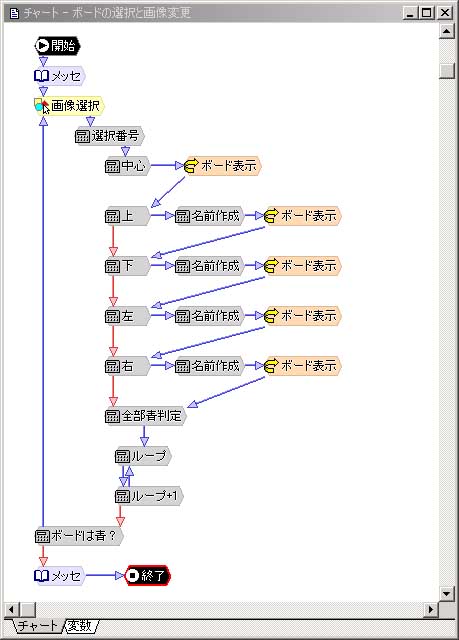
形はさきほどの「☆ボードの初期設定」と似ています。
行っている処理も似たようなもので、指定したパネルの色を変化させ、それを表示しているだけです。
もちろん上下左右のパネルの有無の判定もしています。
判定が終わり、パネルが表示されましたら、ループに入ってボード[0]〜[24]のカラー番号をすべて加算しています。
もし、合計が2（もしくは3）以下ならば、ほとんどが青パネルなのでゲームクリアとなり、終了します。

このチャートでのポイントは、＜画像選択＞にあります。
＜画像選択＞でパネルを選んでいるのですが、よく見ると、進行先の矢印が一つしかありません。
これでどうやってパネルを判断しているのかと言いますと、「選択されたときに出力される『選択番号』をそのまま『ボード番号』として扱っている」のです。

※計算-選択番号：選択番号を仮受変数に代入


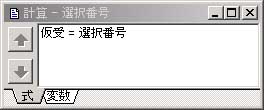
こうすることにより、余計な手順を減らし、かつ配列変数の強みを利用しているのです。

☆統括
さて、これで一連の流れは説明しました。
まとめに入りましょう。
今回の講座のポイントは3つです。

　１、配列変数の概念と利用法
　２、除算の「余り」の使い方
　３、＜画像（文字列）選択＞の「選択番号」活用法

これがわかれば、単純なボード系ゲームは作れるのではないでしょうか。
みなさんも、ぜひチャレンジしてみてください。


☆おまけの「ボード表示」
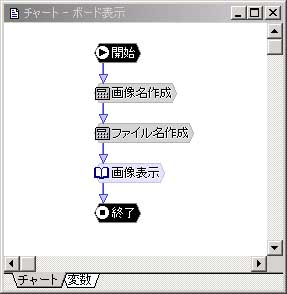
今回、説明はしませんでしたが、わたしがゲームを作るさいは下のような画面表示専用のチャートを用意しています。
画像表示に変数が使えるので、専用チャートを用意することで同じものを何度も作らずにすんで便利です。
「文字列変数」の結合しか行っていませんので、興味がおありの方はお試しください。

※チャート-ボード表示



毎度、早足ながらこれで解説を終わりたいと思います。
何かご質問等ありましたら、お気軽にメールをください。



　　　　ホームへ戻る