◎　サイクルのあるものの数理モデル化について

　波形モデルとは、sinやcosなど三角関数を利用するモデルのことです。
　周波数、円の成分、波の性質を持つモデルと言い換えても構いません。
　従来、多くの統計や経済モデルは、線形近似モデルを使ってきました。
　しかし、人の活動には、ある目的を決めたら、まっすぐ！という活動もあれば、
　予習をし、実行し、反省し、もういちど少し違う角度からトライして、
　というサイクルを持つ活動もあります。

　もしも、対象となるモデルがこのような波形の性質があるモデルならば、
　あるときの趨勢だけを分析して、その方角にまっすぐな努力をしてみる
　ことは、本質を失う原因になる可能性があります。
　それは、丁度、音楽のある一瞬の音をいくつかひろっただけで、
　楽曲全体を判断しようとするものです。
　サイクル全体を分析してして、その周波数を合わせて活動する
　ことが、より正しい理解へ導くといえます。

　とくに、ビジネスや教育や、リサイクル、など、「サイクル」のある人間の
活動はたくさんあります。
　つまり、評価・FeedBackなど、結果をさらに自分のInputとするものは、
すべて、こうした円の性質を持ったモデルを使うことに意味がありそうです。

　線形モデルでは、ベクトル（方向）とスカラー（量）が大切でした。
　周波成分を持つということは、さらに、周期という考え方が出てきます。
　そして今は、その周期のどの位相（フェーズ）であるか？を、
　把握する必要が出てきます。

　例えば、下図のようなモデルを考えてみましょう。

　縦軸に成果、　横軸に時間　をとって、
　Sinカーブを書きます。
　（図１）

　ある製品の作成サイクルについてこのような図ができたとして、
実際の製品はもっとたくさんのサイクルの和になるので、きっと
人の音声の波のようにぎざぎざになることでしょう。

　上記のモデルでは縦軸に価値、横軸に時間を置いてみました。
　本質的には、別なものを表現するのに使うと便利そうです。
　複素数を使うと、もっとおもしろいモデルを作ることができます。


　　　　　　　　　　　　　　　　　　　　　　　　　　　　2001・2・04　Hattori.

　ご参考▼射影としての三角関数のグラフ　（外部リンク：「数学玉手箱」　早苗　雅史　氏）


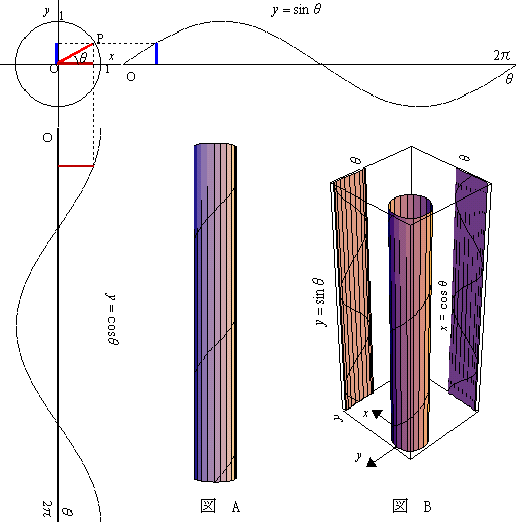
　ご参考▼波の基本操作

　　　・波形の合成　（外部リンク：「数学玉手箱」　早苗　雅史　氏）
　　　・波形の分解　（フーリエ変換：　外部リンク：「数学のいずみ」　早苗　雅史　氏）
　　　　　More　→　FFTアナライザについて▼１▼２　　（外部リンク：小野測器　社）