グラフを描けば良い、というものではない。
グラフを描く、方法論そのものが問題になる。
わらし:でだ、ここからが本題だ。
ミラ:おう、いきなり対話形式か。
わらし:まあ、色々と試行錯誤しているんだ。さて、先にシンプル・イズ・ベスト、という話やグラフを描く、という話をしたな?=>*
ミラ:データを説明できる仮説は無限にある。無限にある候補から良い仮説を選ぶために、最節約とかシンプル・イズ・ベストとか、そういう基準がある、そんな話をしたわね。
わらし:さらにデータを集めることで仮説が妥当かどうか? それを検証する話になったな?
ミラ:なったわね。
わらし:検証するにはグラフを描くことが必要だ。
ミラ:?
わらし:どうした?
ミラ:いやその、それ、当たり前じゃね?
わらし:うん、当たり前だな。だけどもここでこう考えよう。以下のようなデータがある。まあ、ある生物、ここではメゲゲットだとするが、この架空生物メゲゲットの年齢と大きさを示したデータだ。
ミラ:はいはい
わらし:でっ、こんなグラフを引いたとするだな。
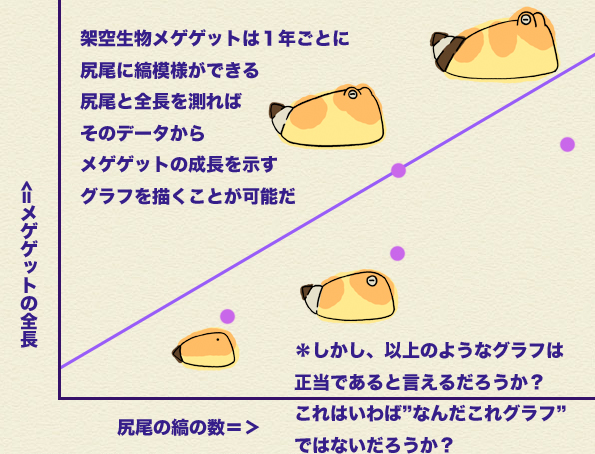
ミラ:いやまて!!
わらし:うん? 何かおかしいか?
ミラ:どう見てもおかしいだろう? なんだこのグラフ?
わらし:なんでだ?
ミラ:なぜこんなひとつだけ外れたデータをわざわざ通るグラフを描く?
わらし:何か問題でも?
ミラ:おおありだろ。このデータ、いかにも怪しいじゃない。
わらし:その根拠はなに?
ミラ:いやだって、他のデータからこれだけ外れていたら、これはいわゆる誤差だろう? 1匹だけやたらと成長が良い個体がまぎれたんじゃないのか?
わらし:他のが誤差じゃね?
ミラ:他の全部が?
わらし:うん? 何か問題でも?
ミラ:そんなのありえないし。
わらし:一人以外、全員勘違いすることはよくある話だがな。
ミラ:でもこれ、生物の成長を示したデータだろ? そういう話とは違うだろうよ。
わらし:ではこのグラフはどうだ?
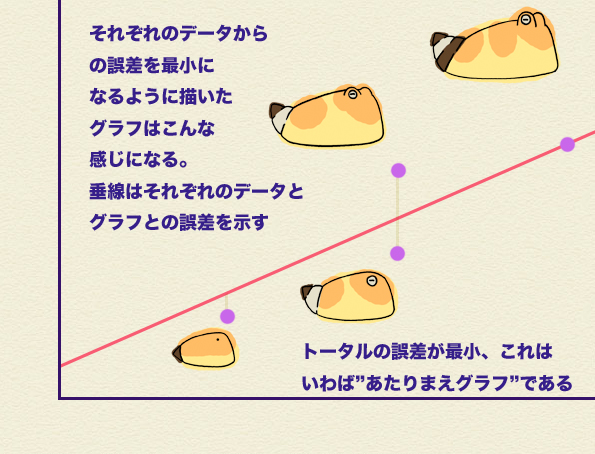
わらし:いかにもあたりまえ、いかにももっともらしいグラフだ。いわば、”あたりまえグラフ”。でも、これだって1つのデータしか通っていないぞ? さっきのと同じでねーか。
ミラ:いやいや待て待て。こっちのグラフの方が、さっきのより誤差が少ないだろうがよ。
わらし:まあ、ようするにあれよね。グラフからデータまでの垂線を引けばそれが誤差なんだけどさ、一目瞭然よね。
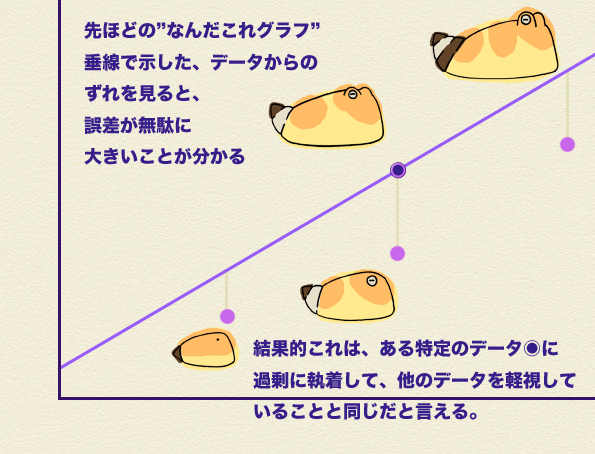
ミラ:さっきの”なんだこれグラフ”はひどいな。
わらし:まあそうだな。実はここからが肝心な部分だ。今、私たちはトータルで誤差が少ないグラフを良しとした。
ミラ:ああ、まあそうだな。
わらし:だけども、採用されなかったグラフを描いた人、ようするに”なんだこれグラフ”を描いた人は納得しないだろうな。
ミラ:なぜ?
わらし:トータルで誤差が少ないグラフを選ばず、わさわざああいうグラフを選んだわけだろ? そこには何らかの理由が、あるいは信念がある。例えばの話、わざわざあのはずれた点を選んだということはだ、あのデータに惚れ込んだのだとも言えるな。
ミラ:まあ、重要視しているんだろうな、それは分かるよ。
わらし:そこが問題になるだよ。
ミラ:なぜに?
わらし:例えばだ、メゲゲットのデータをさらにとって見ると次のようになった。
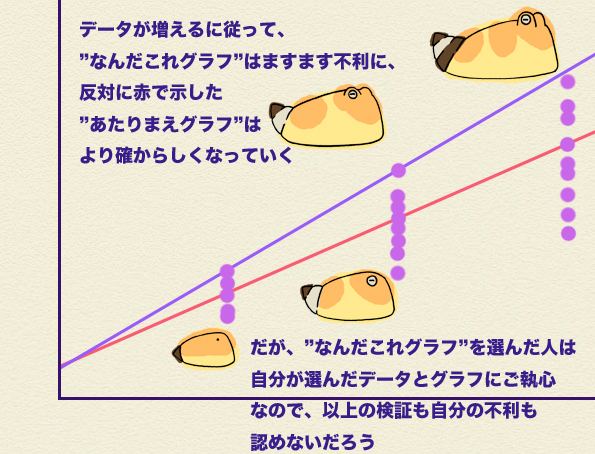
わらし:お前さんならどうするね?
ミラ:そりゃあ、誤差が少ないと選んだグラフ、図では赤で示されている奴よね、これをこのまま良しとするわよ。
わらし:だけどもさ、採用されなかった”なんだこれグラフ”を描いた人は納得しないだろうな。
ミラ:なぜに?
わらし:最初のあのデータにご執心なんだろ? 新しいデータの山ごときでくじけると思うか?
ミラ:ああ、うーん、くじけて欲しいが、くじけないだろうね。
わらし:次々にデータを加えて、やっぱトータル誤差最小のグラフが良いらしいと分かってきた。
ミラ:検証されているわけよね。
わらし:でも、彼の人はあきらめないだろうな。
ミラ:ご執心だからか?
わらし:ご執心だからね。
ミラ:でもさ、それってトンデモじゃね?
わらし:これがトンデモの仕組みなんじゃねえの?
ミラ:あー、うーん....
わらし:彼の人にとってはトータル誤差最小のグラフなんて意味ないだろうな。
ミラ:なぜ? ご執心だからか?
わらし:ご執心だからだ。彼にとってはこうだ、オレはこのデータが良いと思っている。そしてこのデータを通るこのグラフが良いと思っている。ようするにあれだ、
:このデータは正しい
:正しいグラフとは正しいデータを通るものである
:ゆえにこのグラフは正しい
まあ、矛盾はないし、極めて論理的である。
ミラ:いや、でもさ、論理的である、だけでは意味なんかないんだろ? 例えば、
:星はチーズで出来ている
:月は星である
:ゆえに月はチーズで出来ている
以上の三段論法には矛盾も無いし、極めて論理的だわよね?
わらし:経験的に明らかに間違っているけどな。
ミラ:でも経験は論理じゃないんだろ?
わらし:ああ。星はチーズで出来ている? そんなの論理的にありえない、という人もいるだろうが、それは間違っている。
ミラ:私たちはすべての星の組成を調べたわけではない。
わらし:調べたわけではない。調べた一部の事柄を星全体に普遍させるのは論理の飛躍だ。スペクトル分析も、それは宇宙と地球が同じ物質で出来ており、同じ法則のもと、同じ振る舞いをするという前提で星の組成を推し量っているだけだ。一部の事柄をなし崩し的に全体に当てはまると考える、これは帰納法だな。論理では正当化できないし、論理の立場から見れば、これは拡大解釈だ。
ミラ:いいかえると、”星はチーズで出来ているわけがない”、という言葉は論理、あるいは論理だけで正当化できる言明ではない。
わらし:だがしかし論理は文章の組立てが正しいというだけの話であって、文章中で申し述べていることを正当化してくれるわけではない。月はチーズで出来ているという以上の三段論法の組立ては正しいが、現実について何も語っていない。
ミラ:だから月がチーズで出来ているかどうかは、現実に調べないと分からない。見方を変えれば、論理論理言っている奴は経験を無視する。論理的に月はチーズで出来ている、論理的に月がチーズであることなどありえない、対立しているがどっちも根っこは同じ、経験の無視だ。お前が以前いったことだよな?
わらし:まあ、そういうことだ。実はこの経験というのがこれまた、今ここにおいて重要でね。
ミラ:なぜに?
わらし:私たちはトータル誤差最小という基準、そこに追加されるデータによってグラフを検証した。グラフというのはデータを説明するもの、いわば仮説だな。事実、私たちは最初に引いたグラフを絶対の真理だなどと思っていたわけじゃない。そうだよな?
ミラ:そりゃあ、真理だとしたらそもそも検討も検証もしないからね。
わらし:つまり”トータル誤差最小”という基準は、追加データで仮説を検証する過程で使えるものだった。データを集めて確かめる。これは経験で確かめるってことじゃないかい?
ミラ:ああ、うーん、そうなるか。
わらし:私たちはおよそ答えを絶対視しない。なんとなくこれが正しいと思っていても、経験して駄目だったら考えを改めるもんさ。
ミラ:できないやつもいるぞ?
わらし:何かに固執しているか、信念があるからだな。
ミラ:さっきの彼の人のようにか?
わらし:彼の人のようにね。そして言い訳が多くなる。なぜか? 簡単さね。彼の人のグラフは誤差が大きかったよな?
ミラ:そうね。
わらし:データを追加したら、誤差のトータルはどうなった。
ミラ:私たちが選んだのもそりゃあ絶対的には増えていたけども、彼の人のものはうなぎ上りと申しますか。
わらし:誤差が増大する。それでも最初のデータとグラフに固執する。だとすると、新しいデータは全部、ここは誤差、ここが誤差、これがまちがっていると言わなければいけない。それもうなぎ上りに増大するのなら、言い訳だってうなぎ上りになるわけだ。「そうならないのは当然です」「こんなデータでは信用できるわけがありません」、理路整然と説明するだろうな。
ミラ:口先だけはいっちょまえにか?
わらし:実際にはぐだぐだな言い訳だけどね。
ミラ:それはもうトンデモだろ?
わらし:つまり、これがトンデモじゃないのかい?
ミラ:あー、うーん。
わらし:なにかに固執して経験というデータを生かせなくなる。データと自分の仮説の齟齬を説明するために言い訳や前提がやたらに多くなる。トンデモというのは単純にいうとデータからグラフは引ける、しかし妥当なグラフは描けない、そういうことなのかもしれない。
ミラ:経験を生かせない、と。
わらし:言い換えるとだ、これこそが本題なんだが、経験を有効なものとして活用するにはグラフを描くだけでは駄目だってことになる。
ミラ:ああ、まあ、トンデモさんもオレ様理論屋さんもグラフ自体は描いているし、データから仮説を導いているのよね。
わらし:そうだ、グラフを描くだけでは駄目なんだ。グラフを描く方法論、それそのものが妥当かどうか? それが重要だ。
ミラ:彼の人やトンデモさんたちは固執したのがいけなかったのかしらね?
わらし:さっき三段論法をしたよな
:このデータは正しい
:正しいグラフとは正しいデータを通るものである
:ゆえにこのグラフは正しい
これでは大前提を疑わない限り、答えの正しさから出られない。しかし自分で選んだデータは絶対的に正しいに違いなく、しかもそれが答えの正しさに直結している。つまり大前提を疑わないことで、答えを疑わないことにしてしまった。ようするに検証を不可能にしているわけだね。
ミラ:それがトンデモであり、それがオレ様理論家だと。
わらし:グラフを答えだと思ったのかもしれん。
ミラ:?
わらし:グラフはデータを説明する仮説で、それは問いを説明する仮説なんだ。言い換えると、グラフが正しいかどうか、それをひたすら検討するというのは、答えではなく、むしろ問いにこそ執着しているのだと言える。
ミラ:さっきの彼の人はグラフや恣意的に選んだデータに固執していたわね。
わらし:それはむしろ自分の導きだした美しい答えに固執しているとも言えるな。
ミラ:たしかに、いくら不利なデータが出てきても、答えを変えないっていうのは問いではなく、答えに執着しているのでしょうね。
わらし:つまりこうではないか? 問いに執着するか、答えに固執するか、そこが科学とトンデモの別れ道なのではないか、そういうことよね。
ミラ:重大な問題なのだと。
わらし:そうだ、グラフよりもむしろグラフを引く方法論、これが重要なんだ。次はそれを検討してみよう。
続く=>工事中