ガウス変換を使った楕円積分の計算の解説 12/3/12更新
0 ガウス変換とはなにか
憶えやすいようにkが大きい側の母数をK,角度をΦと大文字で表し kが小さい側の母数をk,角度をφと小文字で表すことにしよう。
sinΦ= S; sinφ= s; cosφ= cと略記しよう。
Kが小さくなる変換を下降ガウス変換、kが大きくなる変換を上昇ガウス変換と呼ぶことにしよう。
ガウス変換とは
下降ガウス変換が k=(1-√(1-K^2))^2/K^2 ; s=((1+k)-√((1+k)^2-4k S^2))/(2k S) (1)
上昇ガウス変換が K=2√(k)/(1+k) ; S=(1+k)s/(1+k s^2) (2)
で表される変数変換のことです。
下降ガウス変換を2回、3回、4回と繰り返した時のkを下添え字をつけてk_2、k_3、k_4と表記しよう。
そして下降ガウス変換を単にガウス変換と表記しよう。
1 ガウス変換を使った第1種楕円積分の計算の解説
第1種楕円積分は図形を長方形化する(被積分関数を定数化する)という原始的な面積計算法が使える例の一つである。
以下の図はアニメーションとは名ばかりで単に静止画を色を変えて重ねて書いたものですが。(≧o≦
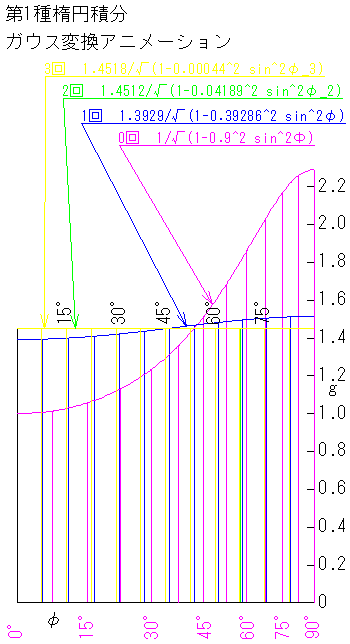
第1種楕円積分 ガウス変換 アニメーション
第1種楕円積分とはE1(Φ,K)= ∫Φ_0 1/√(1-K^2 sin^2Φ) dΦの形の積分で振り子の周期の問題などに現れる。
被積分関数 g=1/√(1-K^2 sin^2Φ)をグラフであらわすと例えばK=0.9のとき
上の第1種楕円積分 ガウス変換 アニメーション図の中の0回と引き出し線を入れたグラフで右上がりの曲線です。
そしてこの原曲線に1回ガウス変換を施すと1回と引き出し線を入れたグラフになり角度を表す縦の線が左に寄り
グラフの左が上がり右が下がる。
原曲線に2回ガウス変換を施すと2回と引き出し線を入れたグラフになりすでに直線だと言っても良い状態になっている。
原曲線に3回ガウス変換を施すと3回と引き出し線を入れたグラフになり2回と3回は重なってしまって
拡大しないと別の曲線である事がわからない。
そして例の場合10桁の精度を出すためには4回があるのだが拡大しても3回と区別出来ないので図には記入しない。
なおK=0.9999999999 程度のときは6回程度ガウス変換を繰り返す必要があります。
第1種楕円積分の面積要素 1/√(1-K^2 sin^2Φ) dΦをガウス変換してみよう
被積分関数部分 g= 1/√(1-K^2 sin^2Φ) のガウス変換は(2)の2番目の式 sinΦ=(1+k) sinφ/(1+k sin^2φ)を代入して
g= 1/√(1-K^2 sin^2Φ)= 1/√(1-(4k/(1+k)^2)((1+k)sinφ/(1+k sin^2φ )^2)= (1+k sin^2φ)/√((1+k sin^2φ)^2-4ksin^2φ))
=(1+k sin^2φ)/(1-k sin^2φ) となる。
K=2√(k)/(1+k)のときだけルートの中が完全平方の形になり根号から出られてこのような簡単な形になる。(^-^
微少巾部分dΦのガウス変換による変化は sinΦ= (1+k) sinφ/(1+k sin^2φ)の両辺を微分すると
dΦ cosΦ= dφ (1+k)(cosφ(1+k sin^2φ )-sinφ(2k cosφ sinφ))/(1+k sin^2φ)^2
= dφ(1+k) cosφ(1-k sin^2φ)/(1+k sin^2φ)^2 となり
cosΦ= √(1-sin^2Φ)= √(1-((1+k)sinφ/(1+k sin^2φ))^2)= √((1+ksin^2φ)^2-(1+k)^2 sin^2φ))/(1+k sin^2φ)
= √((1-sin^2φ)(1-k^2 sin^2φ))/(1+k sin^2φ)= cosφ√(1-k^2 sin^2φ)/(1+k sin^2φ) であるから
dΦ= dφ((1+k) cosφ(1-k sin^2φ)/(1+k sin^2φ)^2)((1+k sin^2φ)/(cosφ√(1-k^2 sin^2φ))
=dφ(1+k)(1-k sin^2φ)/((1+k sin^2φ)√(1-k^2 sin^2φ)) となる。
微少巾部分と被積分関数部分を掛けた面積要素のガウス変換は
g dΦ=((1+k sin^2φ)/(1-k sin^2φ))dφ(1+k)(1-k sin^2φ)/((1+k sin^2φ)√(1-k^2 sin^2φ))=(1+k)/√(1-k^2 sin^2φ) dφ となり
積分すると
∫Φ_0 1/√(1-K^2 sin^2Φ) dΦ= ∫φ_0 (1+k)/√(1-k^2 sin^2φ) dφ となるから
第1種楕円積分は下降ガウス変換によって大きさの係数が(1+k)倍になり母数がKよりも小さい母数kとなり積分区間がΦよりも小さいφの
第1種楕円積分に変換される事がわかる。グラフの右側が下がって左側が上がり長方形に近くなる。
そしてkが実用上0となるまで変換を繰り返せば(例の場合4回)大きさの係数aは a=(1+k)(1+k_2)(1+k_3)(1+k_4) となり
グラフを長方形化出来て(被積分関数が実用上定数になる)高さ方向の巾aと横方向の巾φ_4を掛けるだけで面積(積分)が計算出来る。(^-^
E1(Φ,K)= ∫(φ_4)_0 a dφ_4= a [φ_4](φ_4)_0= a φ_4
2 21a展開を使った第2種楕円積分の計算の解説
第2種楕円積分とは∫Φ_0 √(1-K^2 sin^2Φ)dΦ の形の積分で楕円の周長の計算などに現れる。
第2種楕円積分はガウス変換を使って長方形化出来る第2種楕円積分と第1種楕円積分、すぐ計算出来る初等関数の和へ展開する事が出来る。
表題があまりに長くなるので第2種楕円積分を2と略記し、第1種楕円積分を1と略記し、初等関数をaと略記し21a展開と略記する事にしよう。
初等関数としてEa(φ,k)= sinφ cosφ√(1-k^2*sin^2φ)/(1+k sin^2φ)が適当。
これは簡易数学公式集のJ2積分を楕円積分と初等関数の和に展開するとき使用した
初等関数Ea3(φ,k,kc)のkcをkと変換したものと同じである。
Ea(φ,k)を微分すると
d/dφ(Ea(φ,k))= (k^3 sin^6φ+3k^2 sin^4φ-(2+k+2k^2)sin^2φ+1)/((1+k sin^2φ)^2 √(1-k^2 sin^2φ)) となる
第2種楕円積分の21a展開アニメーション
被積分関数 f=√(1-K^2 sin^2Φ)をグラフであらわすと例えばK=0.9のとき
上の第2種楕円積分のガウス変換を使った21a展開アニメーション図の中の
0回と引き出し線を入れたグラフで右下がりの曲線です。
そしてこの原曲線に1回ガウス変換を施すと1回と引き出し線を入れた実線のグラフになり角度を表す縦の線が左に寄りグラフの左が上がり右が下がる。
実線と同じ色の点線の曲線は第2種楕円積分と第1種楕円積分の被積分関数の和を表したグラフです。
原曲線に2回ガウス変換を施すと2回と引き出し線を入れたグラフになり点線はすでに直線だと言っても良い状態になっている。
原曲線に3回ガウス変換を施すと3回と引き出し線を入れたグラフになり2回と3回は重なってしまって拡大しないと別の曲線である事がわからない。
そして10桁の精度を出すためには4回があるのだが拡大しても3回と区別出来ないので図には記入しない。
第2種楕円積分の面積要素 √(1-K^2 sin^2Φ)dΦをガウス変換しよう
被積分関数 f= √(1-K^2 sin^2Φ) のガウス変換は sinΦ=(1+k) sinφ/(1+k sin^2φ)を代入して
f=√(1-K^2 sin^2Φ)= √(1-(4k/(1+k)^2)((1+k)sinφ/(1+k sin^2φ )^2)= √((1+k sin^2φ)^2-4ksin^2φ)/(1+k sin^2φ)
=(1-k sin^2φ)/(1+k sin^2φ) となる
微少巾部分dΦのガウス変換による変化は上の(3)式と同じでdΦ= dφ(1+k)(1-k sin^2φ)/((1+k sin^2φ)√(1-k^2 sin^2φ)) となる
面積要素をガウス変換したものは
f dΦ=(1+k)(1-k sin^2φ)^2 dφ/((1+k sin^2φ)^2 √(1-k^2 sin^2φ))
=(1+k)(k^2 sin^4φ-2k sin^2φ+1) dφ/((1+k sin^2φ)^2 √(1-k^2 sin^2φ))=A となる
これを未定の係数をα、β、γとして第2種楕円積分の被積分関数√(1-k^2 sin^2φ)と第1種楕円積分の被積分関数1/√(1-k^2 sin^2φ)と
初等関数を微分した関数d/dφ(Ea(φ,k))= (k^3 sin^6φ+3k^2 sin^4φ-(2+k+2k^2)sin^2φ+1)/((1+k sin^2φ)^2 √(1-k^2 sin^2φ)) の和で表わしBにしたい。
B=α √(1-k^2 sin^2φ)+β/√(1-k^2 sin^2φ)+γ(k^3 sin^6φ+3k^2 sin^4φ-(2+k+2k^2)sin^2φ+1)/((1+k sin^2φ)^2 √(1-k^2 sin^2φ))
Bを通分するとB=(α(1-k^2 sin^2φ)(1+k sin^2φ)^2+β(1+k sin^2φ)^2+γ(k^3 sin^6φ+3k^2 sin^4φ-(2+k+2k^2)sin^2φ+1))/((1+k sin^2φ)^2 √(1-k^2 sin^2φ))
=(α(1-k^2 sin^2φ)(1+k sin^2φ)^2+β(1+k sin^2φ)^2+γ(k^3 sin^6φ+3k^2 sin^4φ-(2+k+2k^2)sin^2φ+1))/((1+k sin^2φ)^2 √(1-k^2 sin^2φ))
= (-k^4α+k^3γ)sin^6φ+((k^2-2K^3)α+k^2β+3k^2γ)sin^4φ+(k(2-k)α+2kβ-(k+2+2k^2)γ)sin^2φ+α+β+γ)/((1+k sin^2φ)^2 √(1-k^2 sin^2φ)) となる。
AとBが等しいとき分母は共通であるから分子のsinφの6次、4次、2次、0次の項の係数が等しい。従って次の4つの式が成り立つ
-k^4α+k^3γ=0; (k^2-2k^3)α+k^2β+3k^2γ=k^2(1+k); k(2-k)α+2kβ-(k+2+2k^2)γ=-2(1+k); α+β+γ=(1+k)
1番目の式からγ=k αとなり残りの3つの式に代入して変形すると(1+k)α+β=(1+k)の同じ形の式が2つ出てきて一方を捨てると
(1+k)α+β=(1+k); -k(1+k)α+β= -(1+k) となる。これを解くと
α= 2/(1+k) ; β= k-1 ; γ= 2k/(1+k) となり
√(1-k^2 sin^2Φ) dΦ= 2/(1+k) √(1-k^2 sin^2φ)+(k-1)/√(1-k^2 sin^2φ)
+(2k/(1+k))(k^3 sin^6φ+3k^2 sin^4φ-(2+k+2k^2)sin^2φ+1)/((1+k sin^2φ)^2 √(1-k^2 sin^2φ))
となる事がわかる。両辺を積分すると
∫Φ_0 √(1-k^2*sin^2Φ)dΦ= (2/(1+k))∫φ_0 √(1-k^2 sin^2φ)dφ+(k-1)∫φ_0 1/√(1-k^2 sin^2φ) dφ
+(2k/(1+k)) sinφcosφ/((1+k sin^2φ)√(1-k^2 sin^2φ))
となり
E2(Φ,K)= (2/(1+k))E2(φ,k)+(k-1)E1(φ,k)+(2k/(1+k)) Ea(φ,k)
と展開出来る事がわかる。
最初は第2種1つの項のみであるが1回変換後には第2種から第2種と第1種と初等関数が出て3つの項になる。初等関数はすぐ計算出来て数値になる。
第2種と第1種は計算出来ないのでさらにガウス変換を繰り返す事になる。そうすると第1種から第1種が出てくるがこれは第2種から出てくる第1種と
同じ物であるから係数を加算してまとめる事が出来て1つの項に出来る。
第2種から出てくる初等関数は計算して前の数値と加算して1つの項に出来るので変換を繰り返しても項数が増えることはなく
何時も3つの項の和で現せる事がわかる。第2種の項の係数をA2,第1種の項の係数をA1,数値をeとして
Kが大きい側のfを f= A2 E2(Φ,K)+A1 E1(Φ,K)+Eと表わすと21a展開によって
a2= (2k/(1+k))A2; a1= (1+k)A1+(k-1)A2; e= E+(2k/(1+k))A2 s c √(1-k^2 s^2)/(1+k s^2) (9)
という漸化式がなりたちKが小さい側のfは f=a2 E2(φ,k)+a1 E1(φ,k)+e と表わされる。
そしてkが実用上0となるまで変換を繰り返せば(例の場合4回)第2種楕円積分の大きさの係数a2はa2_4となり
第1種楕円積分の大きさの係数a1はa1_4となり初等関数部分はe_4となり
第2種楕円積分と第1種楕円積分の和のグラフを長方形化出来て高さ方向の巾aをa=a2_4+a1_4と略記すれば横方向の巾φ_4を掛けるだけで面積(積分)が計算出来
E2(Φ,K)= ∫(φ_4)_0 (a2_4+a1_4) dφ_4+e_4= a [φ_4](φ_4)_0+e_4= a φ_4+e_4となる。(^-^
3 ガウス変換を使った第3種楕円積分の計算の解説
第3種楕円積分の被積分関数はガウス変換によって定数化出来る第1種楕円積分の被積分関数とガウス変換後も積分可能な分数との積に表される。
第3種楕円積分とは∫Φ_0 1/((1+KC sin^2Φ)√(1-K^2 sin^2Φ)) dΦ の形の積分で
第1種楕円積分の被積分関数の部分g=1/√(1-K^2 sin^2Φ)とsinΦの分数f=1/(1+KC sin^2Φ)との積で表される。(KCはパラメタと呼ばれる)
第3種楕円積分 ガウス変換 アニメーション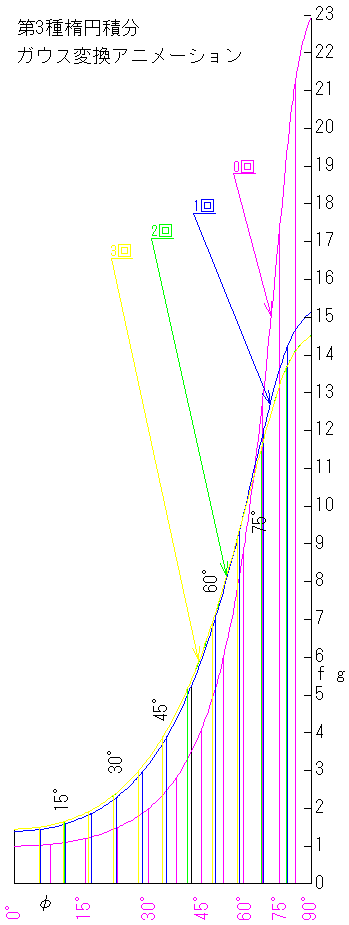
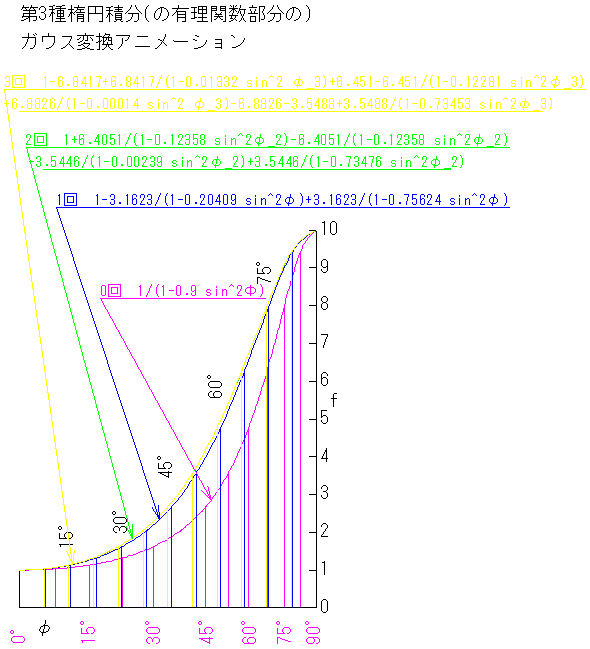
被積分関数 1/((1+KC sin^2Φ)√(1-K^2 sin^2Φ))をグラフであらわすと例えばKC=-0.9;K=0.9のとき
上の第3種楕円積分 ガウス変換 アニメーション図の中の0回と引き出し線を入れたグラフで右上がりの曲線です。
g=1/√(1-0.9^2 sin^2Φ)の右上がり度にf=1/(1-0.9 sin^2Φ)の右上がり度が掛かる事になるので非常に右上がり度が大きくなっている。
もちろんKCは正でも負でも良いからKCが正のときには打ち消し合っておだやかな曲線になる。
そしてこの曲線に1回ガウス変換を施した物が図の中の1回と引き出し線を入れたグラフで角度を表す縦の線が左に寄り
グラフの左が上がり右が下がっている。
曲線に2回ガウス変換を施した物が図の中の2回と引き出し線を入れたグラフです。
曲線に3回ガウス変換を施した物が図の中の3回と引き出し線を入れたグラフで2回と3回は重なってしまって拡大しないと別の曲線である事がわからない。
そして10桁の精度を出すために4回目があるのだが拡大しても3回と区別出来ないので図には記入しない。
fにガウス変換を施してみよう。
f=1/(1+KC sin^2Φ)= 1/(1+KC((1+k) sinφ/(1+k sin^2φ ))^2)= (1+k sin^2φ)^2/((1+k sin^2φ)^2+KC (1+k)^2 sin^2φ)
= (k^2 sin^4φ +2k sin^2φ +1)/(k^2 sin^4φ +(2k+KC(1+k)^2)sin^2φ +1)
分子 (k^2 sin^4φ +2k sin^2φ+1) から分母 (k^2sin^4φ +(2k+KC(1+k)^2)sin^2φ+1)を引くと -KC(1+k)^2 sin^2φであるから
f=1-KC(1+k)^2 sin^2φ/(k^2 sin^4φ+(2k+KC(1+k)^2)sin^2φ +1)
分数の項の分母が sinφの 4次式になったので部分分数に展開するため分母を因数分解する。
分母= k^2 sin^4φ+(2k+KC(1+k)^2)sin^2φ+1= 0と置き sin^2φについて方程式を解くと
sin^2φ= (-(2k+KC(1+k)^2)±√((2k+KC(1+k)^2)^2-4k^2))/(2k^2)=(-mo±rt)/(2k^2) ((2k+KC(1+k)^2)=moと略記; √((2k+KC(1+k)^2)^2-4k^2)=rtと略記)
分母は分母=k^2(sin^2φ+(mo-rt)/(2k^2))(sin^2φ+(mo+rt)/(2k^2)) と因数分解出来る。
KCが負の値であって (2k+KC(1+k)^2)^2-4k^2 < 0 であっても複素数を使えば出来る。したがって分数fは
f=1+KC(1+k)^2/(2rt k^2)((mo-rt)/(sin^2φ+(mo-rt)/(2k^2))-(mo+rt)/(sin^2φ+(mo+rt)/(2k^2)))
=1+(KC(1+k)^2/rt)(1/(1+(2k^2/(mo-rt))sin^2φ)-1/(1+(2k^2/(mo+rt))sin^2φ) と部分分数に展開できる。
さらに部分分数のsin^2φの係数の分子、分母に (mo+rt)または(mo-rt)を掛けると
f=1+(KC(1+k)^2/rt)(1/(1+(2k^2(mo+rt)/(mo^2-rt^2))sin^2φ)-1/(1+(2k^2(mo- rt)/(mo^2-rt^2))sin^2φ)となるが mo^2-rt^2=4k^2であるから
f=1+(KC(1+k)^2/rt)(1/(1+((mo+rt)/2)sin^2φ)-1/(1+((mo-rt)/2)sin^2φ)
これからfは定数1と係数が±KC(1+k)^2/rt パラメタが kc= (mo±rt)/2 である二つの分数に分かれる事がわかる。
さらにガウス変換するとそれぞれの分数から定数1と新しいパラメタを持つ二つの分数が現れるが定数1は打ち消しあって消え分数の数が2倍になる。
kが実用上0となるl回まで(今は4回)ガウス変換を繰り返せばgdΦは 大きさの係数をaとしてa dφ_4となるので
最初の定数1を積分したものと各分数を公式∫Φ_0 dΦ AC/(1+KC sin^2Φ)= arctan(SK tanΦ)/SK (√(1+KC)= SK と略記)を使って
積分して加算したものにaを掛ければ元の積分の答になる。(^-^
fの部分のみのガウス変換の様子を表わしたグラフを次に載せます。
第3種楕円積分(の有理関数の部分の)ガウス変換 アニメーション