場の持つエネルギーと質量 (その1) 重力場の持つエネルギーと質量
0電場と重力場の関係
まず最も古くから知られている重力場のおさらいをしよう。
f=Q q/(4πεl^2) 電気力の場合のクーロンの法則と
f=-G M m/l^2 ニュートンの引力の法則を比較して(普通は符号-はついていないがここでは引力と言う事であえてつけよう)
1/(4πε)= -Gと対応することがわかる
したがって電場に関する式の誘電率εをε=-1/(4πG)と置き換えQをM と置き換えqを mと置き換えれば重力場による式になる事がわかる。
電場E_と電束密度D_はE_ =D_/εの関係にあるから
重力場f_と重力束密度Dg_はf_ =-4πG Dg_の関係になる
1広い重力板2枚を使って均一重力場と無重力場を作り重力場の単位体積あたりの重さを計算する
他に重力場の無い宇宙空間に無限に広い(厚みに比べて十分広い)二枚の重力板を重力板同士がくっついてしまわないように
メカで一様なすきま保つようにして浮かべる
もちろん無限に広がっている面積あたりの質量密度が均一の重力板というようなものを考えると質量が無限大になって物理的に破綻するが
単位面積あたりの質量というように考えれば計算を進めることが出来る。重力板に垂直な方向をz方向としよう。
1-1薄い重力板による重力場の計算
薄い重力板による重力場の計算の座標、変数図

まず単位面積あたりの質量がσである薄い重力板による重力場の計算をしよう。重力板の芯からz方向にhの距離にある重力場の測定点Pから
重力板に垂線を立て垂線が重力板と交わる点をOとしよう。
O点を中心とした内半径と外半径の平均がr、微少巾drの円形リングを重力板から抜き取りさらにリングの平均半径上の任意の点をQ点としよう。
P点とQ点の間の距離をRとするとQ点周辺の単位質量がP点にある単位質量の物質に及ぼす力frs_はP点からQ点に向かう方向で大きさは
Q点からP点に向かう方向を正として fr_=-G/R^2
∠OPQ=χとすればcosχ=h/R であるからfrs_のz方向成分frs_zは
frs_z= frs_ cosχ= -G h/ R^3 となる。
リングの質量は2πr drσであるからリングによるP点にある単位質量の物質に及ぼす力fr_のz方向成分fr_zは
fr_z = -Gσh 2πr dr/R^3となる。
fr_の円板に平行方向の成分は打ち消し合って0となるので考える必要がない。
fr_zをr =0から∞まで積分するとhが正のとき重力板がP点にある単位質量の物質に及ぼす力(重力場の強さ)のz方向成分 f_zは
f_z =-2πGσh∫∞_0 dr r/R^3
r^2+h^2= R^2であるから両辺をrで微分してr dr = R dR である。この関係を利用してrによる積分をRによる積分に変えることが出来る。
f_z =-2πGσh∫∞_h dR R/R^3=-2πGσh∫∞_h dR/R^2= 2πGσh [1/R]∞_h 0=-2πGσ (1) となりhにかかわらず一定である事がわかり
h=0のときはf_z =0
hが負のときはf_z =2πGσ となりhにかかわらず一定である事がわかる。
この結果を重力管の観点から考えると単位面積あたりの質量がσである薄い重力板から出る重力管の総量はσ(kg)、重力管はzのプラス側とマイナス側に等量出て行くので
zがプラス側へ出て行く重力管の数はσ/2 (kg)従って単位面積あたりの重力管の密度=重力束密度Dg_zはDg_z=σ/2
重力場の強さはf_ =-4πG Dg_の関係からf_z =-4πG Dg_z=-4πG(σ/2) =-2πGσとなり(1)式の結果が簡単に出てくる。
zがマイナス側に出て行く重力管の数は方向が逆なので-σ/2 (kg)と数え重力場の強さはf_z =-4πG Dg_z=-4πG(-σ/2) =2πGσとなる。
1-2厚い重力板による重力場の計算
重力板の厚み⊿とし簡単のため重力板の密度は一定密度ρとする。重力板の芯をz座標の0点とする。
⊿/2< zのとき σ=ρ⊿の重力板が測定点よりマイナス側にあるから f_z =-2πGσ=-2πGρ⊿
-⊿/2<z<⊿/2のとき 測定点よりプラス側にある部分の厚みは(⊿/2-z) 測定点よりマイナス側にある部分の厚みは(z+⊿/2)であるから
f_z =2πGρ((⊿/2-z)-(z+⊿/2))= -4πGρz
z<-⊿/2のとき σ=ρ⊿の重力板が測定点よりプラス側にあるから f_z = 2πGρ⊿
2枚の重力板を使って重力場の重さを計算する図
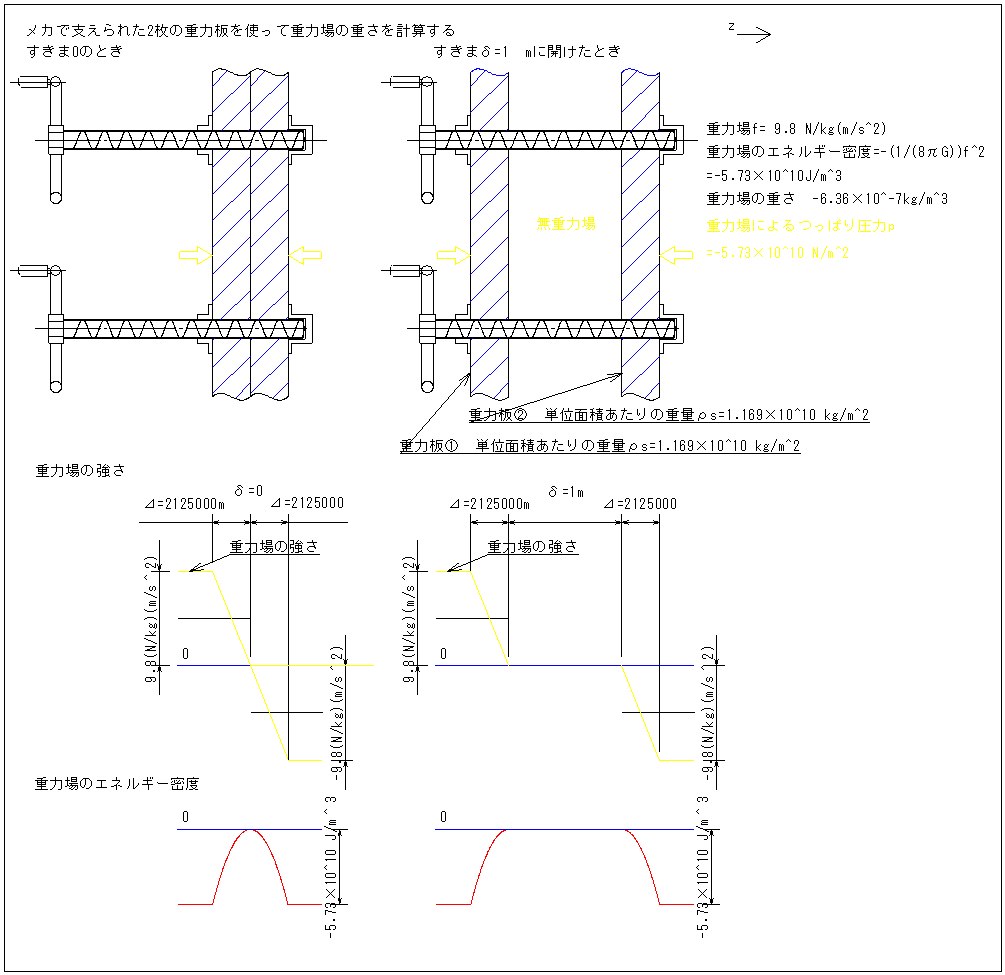
1-3メカで支えられた2枚の重力板による重力場の計算
一定密度ρで厚み⊿の重力板2枚をδの隙間をとって並べz座標でマイナス側にあるものを重力板①プラス側にあるものを重力板②とし
重力板①の芯をz座標の0点とする。重力場は重力板①による重力場と重力板②による重力場を加算したものになるから各区間での重力場は
δ+3⊿/2< zのとき σ=2ρ⊿の重力板が測定点よりマイナス側にあるから f_z =-2πGσ=-4πGρ⊿
δ+⊿/2< z <δ+3⊿/2のとき σ=ρ⊿の重力板が測定点よりマイナス側にありそれに②の板の中の重力場を加えてf_z = -2πGρ⊿-4πGρ(z-δ-⊿)
=-4πGρ(z-δ-⊿/2)
⊿/2< z <δ+⊿/2のとき両側に重力板があり打消しあうから f_z =0
-⊿/2<z<⊿/2のとき σ=ρ⊿の重力板が測定点よりプラス側にありそれに①の板の中の重力場を加えてf_z = 2πGρ⊿-4πGρz=-4πGρ(z-⊿/2)
z<-⊿/2のとき σ=2ρ⊿の重力板が測定点よりプラス側にあるから f_z = 4πGρ⊿
1-4メカで支えられた2枚の重力板による重力場のエネルギーの計算
電場のとき単位体積あたりのエネルギー密度EdはEd= (1/2)ε(E_・ E_)と表されるが(ここでE_・E_はベクトルE_とE_の内積E_x E_x+ E_y E_y+ E_z E_zを表わしています)
重力場のときはε=-1/(4πG)、E_=f_と置き換えればよい( f_・f_=(f_x)^2+(f_y)^2+(f_z)^2)
(1/2)ε(E_・ E_)= -(1/2)(f_・f_)/(4πG)=-(f_・f_)/(8πG)となり単位体積あたりのエネルギー密度EdgはEdg=-(f_・f_)/(8πG) (11) で計算出来る。
各区間での重力場のエネルギー密度は
δ+3⊿/2< zのとき Edg=-(f_・f_)/(8πG)= -(-4πGρ⊿)^2/(8πG)=-2πGρ^2⊿^2
δ+⊿/2< z <δ+3⊿/2のとき Edg=-(f_・f_)/(8πG)= -(-4πGρ(z-δ-⊿/2))^2/(8πG)=-2πGρ^2(z-δ-⊿/2)^2⊿^2
⊿/2< z <δ+⊿/2のとき Edg= 0
-⊿/2<z<⊿/2のとき Edg=-2πGρ^2(z-⊿/2)^2⊿^2
z<-⊿/2のとき Edg=-2πGρ^2⊿^2
単位面積当たりの重力場全体のエネルギーEtは無限大になって考えられないのですきまδを0からδまで拡げる時の重力場全体のエネルギーの変化分⊿Etを考えよう。
このとき重力板の内部の重力場のエネルギーは変わらず重力板②の外側の重力場がδの厚さだけ減って内側の無重力場がδの厚さだけ増えることになるから
単位面積当たりの重力場全体のエネルギーの増加分は⊿Et= -(-2πGρ^2⊿^2)δ=2πGρ^2⊿^2δ となる
重力板①が重力板②の所へ作る重力場はf_z =-2πGσ=-2πGρ⊿ で重力板②の単位面積当たりの質量はσ=ρ⊿であるから
重力板②が重力板①に引っ張られる単位面積当たりの力FはF=f_zσ=-2πGρ^2⊿^2
重力板②を引っ張ってすきまをδまで拡げるに要するエネルギー⊿Ehは単位面積当たり⊿Eh= Fδ=2πGρ^2⊿^2δ となり⊿Et=⊿Ehである事が確認出来る。
ここで具体的に数値を入れて計算してみよう。
重力板の外側の重力場を地球の表面での重力場-9.8 m/s^2に等しくするには密度ρを地球の平均密度ρ=5500 kg/m^3と等しいとすると
f_z =-4πGρ⊿=-4π×6.67×10^-11×5500×2125000=-9.8であるから⊿は
⊿=-9.8/(-4π×6.67×10^-11×5500)=2125000 m となる (6375000/3=2125000で地球の半径の1/3)
重力板の単位面積あたりの重量はρ⊿=1.169×10^10 kg/m^2
重力場のエネルギー密度は Edg=-2πGρ^2⊿^2=-2π×6.67×10^-11×5500^2×2125000^2=-5.73×10^10 J/m^3
重力場によるつっぱり圧力は重力場のエネルギー密度と等しく -5.73×10^10 N/m^2
(これは弱いメカではとても支えられるような値ではなくて地球表面での値がなじみがあるので憶えやすかろうと
無理をしてすごい厚みの板にしたからすごい値が出てくるのです。
実際に実現できるのはせいぜい⊿=21.3 m 程度であろうから値は10万分の1になり⊿^2は1/10^10になりEdg=-5.73 N/m^2になり
なんとか手応えが感じられる程度の引っ張り力になる)
重力場の重さ密度は重力場のエネルギー密度をc^2で割って -6.36×10^-7 kg/m^3
すきまδを0から1 mまで拡げる時
単位面積当たりの重力場全体のエネルギーの増加分は⊿Et=2πGρ^2⊿^2δ=5.73×10^10 J/m^2
これはメカに加えるべきエネルギー⊿Ehに等しい
2星の自己重力場のエネルギーの計算
小さい星では密度は一定だとしてもよいが大きな星では中心部が重力によって圧縮されて密度が大きい場合もあろうから
密度は球対称で半径Rの球面上で一定で密度をρ(R )としよう
星の外半径をbとしよう。
2-1星の重力場の計算
星の重力場の計算の座標、変数図

次にやる核力場の計算の練習のためにあえてニュートンの引力の法則で直接計算してみよう。星の中心点をQ点としよう。
星の重力場を測定する地点をP点とし中心からの距離をrとしよう。
半径Rの球面上で重力場を測定する地点から等距離uのリング上の点をR点としよう。
余弦法則よりu^2= R^2+r^2-2R r cosχ
両辺をχで微分すると
2 u du/dχ=2R r sinχ
したがって sinχdχ=u du/(R r) であることがわかる。この式を使ってχによる積分をuによる積分に換える事が出来る。
まずR一定の球面上でχで積分しその後Rで積分しよう。
b < rのとき
f_r =- G∫b_0 dR ρ(R )∫π_0 2πR^2 cos w sinχdχ/u^2
余弦法則よりR^2= r^2+u^2-2r u cos wであるからcos w =(r^2+u^2-R^2)/(2r u) これを代入し
sinχdχ=u du/(R r)を使ってχによる積分をuによる積分に換えると
f_r =-2πG∫b_0 dR ρ(R )∫(r+R)_(r-R) du (R^2 u)(r^2+u^2-R^2)/((R r)(2r u)u^2)= πG∫b_0 dR ρ(R )∫(r+R)_(r-R) (r^2-R^2+u^2)du/(r^2 u^2)
= - (πG/r^2)∫b_0 dRρ(R ) R∫(r+R)_(r-R) (r^2-R^2+u^2)du/u^2= (πG/r^2)∫b_0 dR ρ(R ) R∫(r+R)_(r-R) (r^2-R^2+u^2)du/u^2
∫(r+R)_(r-R) (r^2-R^2+u^2)du/u^2=[-(r^2-R^2)/u+u] (r+R)_(r-R) =4R (1) であるから f_r =- (G/r^2)∫b_0 4πdR ρ(R ) R^2
∫b_0 4πdR ρ(R ) R^2=M (2) であるから f_r =-GM /r^2 (3)となる
0 <r < bのとき
測定点よりも外部にある球面部分による引力は (1)式で積分の下限値を(r-R)から(R-r)に変えれば良いから
∫(r+R)_(R-r) (r^2-R^2+u^2)du/u^2=[-(r^2-R^2)/u+u] (r+R)_(R-r) =0 (1)
となり外部にある球面部分による引力は打ち消しあって0である事がわかる。
従って測定点よりも内部にある球体部分による引力のみ考えれば良い。それは(2)式でbをrに変えれば良いから
f_r =- (G/r^2)∫r_0 4πdR ρ(R ) R^2 となる。
ρ(R )が一定値ρのときには∫r_0 4πdR ρ R^2=4πρr^3/3 となり f_r =-4πGρr/3 となる
さらに4πρb^3/3=Mからρ=3M/(4πb^3)であるからf_r =-4πG(3M/(4πb^3))r/3=-GM r/b^3 (4)
以上の結果を重力管の観点から考えると
星の外では質量M(kg)の星から出てくる重力管の総量はM(kg)で測定点のある半径rの球面の面積は4πr^2であるから
単位面積あたりの重力管の密度=重力束密度Dg_rはDg_r= M/(4πr^2) 重力場の強さはf_r =-4πG Dg_r=-4πG M/(4πr^2) =-GM /r^2
星の中では測定点のある半径rの球面から星の外面までの間にある質量から出る重力管は質量が完全に球対称に分布している場合には
半径rの球面より内には打ち消しあって入れないから考える必要は無い。(非対称の場合には考える必要がある)
従って出てくる重力管の総量は∫r_0 4πR^2 dR ρ(R )であるから重力束密度Dg_rは Dg_r= (∫r_0 4πR^2 dR ρ(R )) /(4πr^2)
重力場は f_r =-4πG Dg_r= -(G/r^2)∫r_0 4πdR ρ(R ) R^2
2-2星の重力ポテンシャルφの計算
f_=-grad(φ)で定義される重力ポテンシャルφを計算してみよう
まずR一定の球面上でχで積分しその後Rで積分しよう。
b < rのとき
φ= -G∫b_0 dR ρ(R )∫π_0 2πR^2 sinχdχ/u
sinχdχ=u du/(R r)を使ってχによる積分をuによる積分に換えると
φ=-2πG∫b_0 dR ρ(R )∫(r+R)_(r-R) du (R^2 u)/(R r u)= -(2πG/r)∫b_0 dR ρ(R ) R∫(r+R)_(r-R) du (5)
∫(r+R)_(r-R) du = [u](r+R)_(r-R)= (r+R)-(r-R) =2Rであるから φ=-(G/r)∫b_0 dR 4πR^2ρ(R ) (6)
∫b_0 dR 4πR^2ρ(R ) = M であるから φ=-G M/r
0 <r < bのとき
重力ポテンシャル測定点の中心からの距離rよりも大きな半径の球面部分による
重力ポテンシャルφ外は(5)式でuによる積分の下限値を(r-R)から(R-r)に変えRによる積分の下限値を0からrに変えれば良いから
∫(r+R)_(R-r) du=[u] (r+R)_(R-r) =(r+R)-(R-r) =2r となり φ外=-G∫b_r dR 4πR ρ(R ) となる。
rよりも小さな球体部分による重力ポテンシャルφ内は(6) 式でRによる積分の上限値をbからrに変えれば良いから
φ内=-(G/r)∫r_0 dR 4πR^2ρ(R )
重力ポテンシャルφは
φ=φ外+φ内=-4πG(∫b_r dR R ρ(R )+(1/r)∫r_0 dR R^2 ρ(R )) となる。
ρ(R )が一定値ρのときには
φ=-4πG(∫b_r dR Rρ+(1/r)∫r_0 dR R^2ρ) =-4πGρ((b^2-r^2)/2+ r^2/3) =-2πGρ(b^2-r^2/3) となる。
2-3星の重力場のエネルギーの計算
(11)より重力場f_の持つエネルギーは単位体積あたり-(1/(8πG))(f_・f_) であり
星の作る重力場の持つエネルギーは星の外部では(3)より
Eo=-(1/(8πG))∫∞_b (4πr^2)(G M/r^2)^2 dr =(1/2)G M^2 [1/r]∞_b=-(1/2)G M^2/b
(∫∞_bはb から∞までの定積分を表しています)
星の内部では(4)より
Ei=-(1/(8πG))∫b_0 (4πr^2)(G M r/b^3)^2 dR =- (1/2)G M^2/b^6 [r^5/5] b_0=-(1/10)G M^2/b
(∫b_0は0から bまでの定積分を表しています)
合わせて重力場の持つエネルギーの総計はE= Ei+Eo=-(1/2)G M^2/b-(1/10)G M^2/b =-(3/5)G M^2/b となる。
ここで具体的に数値を入れて計算してみよう。
まず地球が出来るときに解放される重力場のエネルギーでどの程度温度が上がるか計算してみよう。
M=5.97×10^24 kg; b=6375000 mであるから
E=-(3/5)×6.67×10^-11×(5.97×10^24)^2/6375000=-2.24×10^32 (J)
地球の熱容量としてアルミニュームの熱容量 880J/K/kgを採用しよう。 (重量あたりの熱容量が大きいので低め側の答えが出る)
温度上昇は2.24×10^32/880/5.97×10^24=42600 (K)
となって集合するだけで溶けて比重による物質の分級が始まるであろう事が予想できる。
次に太陽が出来るときに解放される重力場のエネルギーでどの程度温度が上がるか計算してみよう
M=1.99×10^30 kg; b=6.96×10^8 mであるから
E=-(3/5)×6.67×10^-11×(1.99×10^30)^2/6.96×10^8=-2.277×10^41 (J)
太陽の熱容量として水素原子の定容熱容量Cv=(3/2)R/1.008= 12500 J/K/kgを採用しよう。
温度上昇は2.277×10^41/12500/1.99×10^30=9150000 915万Kとなる。
太陽の中心部温度は1500万Kといわれるからそれより少し低い温度になるが桁が近いことで満足してここではこれ以上詮索しないことにしよう。(^^;
3星と星との間に働く引力と相互重力場のエネルギーの計算
3-1大きさのある星と星との間に働く引力
大きさのない質点の間に働く引力は最初に掲げたf=-G M m/l^2であるが
大きさのある球体 星と星との間に働く引力をニュートンの引力の法則を使って直接計算して見よう。
二つの星の内部の密度は半径によって変わるが球対称であるとしよう。
星と星との間に働く引力の計算の座標、変数図
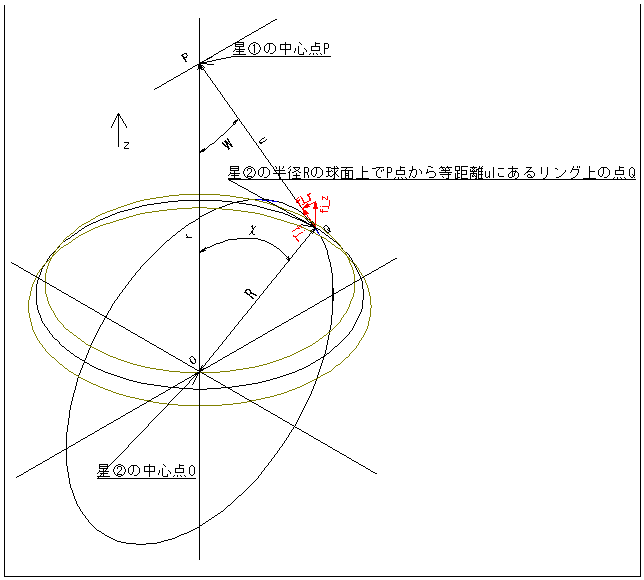
星①の中心点をP点としよう。星②の中心点をO点としPOの距離をrとしよう。星①の外半径をb1、星②の外半径をb2としよう。
星②の半径Rの球面上でP点から等距離uのリング上の点をQ点としよう。
星①の総計した質量をMとし星②の総計した質量をmとしよう。
Q点にある単位質量に働く星①の重力場による力fj_はQP方向で大きさfjは(3)のrにuを代入し
fj =-GM /u^2 であるからPO方向の分力fj_zは fj_z=-GM cos w/u^2
PO方向に直行する方向の力はリング上で打ち消しあって0である。
リングの質量は2πdRρ(R ) R^2 sinχdχであるから星②が星①の重力場にから受けるPO方向の力は
f =-∫b2_0 dR ρ(R )∫π_0 2πR^2 cos w sinχdχG M/u^2
2-1と同様な計算をすると
f = -GM /r^2∫b2_0 4πR^2 ρ(R )dR となる
∫b2_0 4πR^2 ρ(R )dR =mであるから
f=- GM m /r^2 となり二つの星の内部の質量分布が球対称であれば
星①の中心点にM、星②の中心点にm の質量が集まっているとした計算に等しい事がわかる。
3-2 星と星が作る相互重力場のエネルギーの計算
次に星①と星②が同時に存在するときの重力場の持つエネルギーについて考えよう。
- (1/(8πG))∫_V (f1_+f2_)・(f1_+f2_) dv = - (1/(8πG))∫_V ((f1_・f1_)+(f2_・f2_)+2(f1_・f2_)) dv (∫_V は領域Vでの体積積分をdvは体積素片を表しています)
第1項と第2項- (1/(8πG))∫_V (f1_・f1_) dvと - (1/(8πG))∫_V (f2_・f2_) dvは前述の星①と星②の自己重力エネルギーである。
第3項 I3= - 1/(8πG)∫_V 2(f1_・f2_) dvは星①と星②が同時に存在するとき追加の重力場の持つエネルギーである。
グリーンの定理∫_V (gradφ1・gradφ2) dv+∫_V (φ1Δφ2) dv =∫_S (φ1 ∂φ2/∂ν) dsを使い
(Δはラプラシアン∂^2/∂x^2+∂^2/∂y^2+∂^2/∂z^2を∫_S は領域Vの表面での面積積分をdsは面積素片を
∂φ/∂νは面積素片に直交する方向のφの偏微分を表しています。
φ1、φ2は星①と星②の作る重力ポテンシャルです。)
I3=- (1/(4πG))∫_V (f1_・f2_) dv=- (1/(4πG))∫_V (gradφ1・gradφ2) dv=(1/(4πG))(∫_V (φ1Δφ2) dv-∫_S (φ1 ∂φ2/∂ν) ds)
∫_S (φ1 ∂φ2/∂ν) dsは星①と星②から十分離れた面を考えれば∫_S (∂φ2/∂ν) dsは定数でありそれに掛かっている重みφ1が0に近づくので0となる。
したがってI3=(1/(4πG))∫_V (φ1Δφ2) dv
電気力学のとき電位ポテンシャルVと電荷密度ρeの関係はΔV=-ρe/εであるからε=-1/(4πG)と書き換えて
重力ポテンシャルφと密度ρの関係はΔφ=4πG ρ となる
従ってΔφ2は星②の外では0
星②の内部では Δφ2=4πG ρ(R)
このようにグリーンの定理を使えばf1_・f2_がφ1 Δφ2と簡単な形になりまた星②の質量が無いところでは計算する必要が無いことがわかる。
しかし星②の質量が無いところにも重力場のエネルギーは存在しているのであり計算を簡単にすませるための方便である事を忘れてはならない。
φ1= -G M/u; dv=2πR^2 sinχdχであるから
I3= (1/(4πG))∫_V (φ1Δφ2) dv= -(1/(4πG))∫b2_0 4πG ρ(R) dR∫π_0 2πR^2 sinχdχGM/u
=-2πG M∫b2_0 ρ(R)∫r+R_r-R R du/r=-(G M/r)∫b2_0 4πR^2ρ(R) dR=-G M m/r
となり星①の中心点にM、星②の中心点にm の質量が集まっているとした計算に等しい事がわかる。
このエネルギーは星②を無限遠点からrの地点まで星①に降ろす時に解放されるエネルギーに等しい。
例題で数値計算をしよう
星①を地球、星②をパチンコ玉としパチンコ店の1階が海抜0 mであるとし豪華なパチンコ店で2階が5 mの高さにあるとしよう。
パチンコ玉の直径は0.011(m) 重量m= 0.0055 kg
地球の中心とパチンコ玉の中心の距離はパチンコ玉が1階にあるときr1=6366200 m 2階に持って上がったとき+5してr2=6366205 m
地球の重量Mは5.97×10^24 kg 、 G=6.67×10^-11 Nm^2/kg^2
パチンコ玉を1階から2階へ持って上る事による地球とパチンコ玉の周辺の重力場のエネルギーの増加量⊿Eは
⊿E= - G M m(1/r2-1/r1) = - 6.67×10^-11×5.97×10^24×0.0055(1/6366205-1/6366200)
= 6.67×10^-11×5.97×10^24×0.0055×5/6366200^2= 0.27 J
質量に換算するためc^2=9×10^16 m^2/s^2で割ると
0.27/9×10^16=3×10^-18 kg
3×10^-18 kgだけ地球とパチンコ玉の周辺の重力場が重くなる。
重力場はもともと負の質量を持っているから地球とパチンコ玉の距離が離れると弱くなって負の質量がへる、ということは正の質量が増えると言う事です。
我々は正の数、負の数という類推から負の質量を持っている物質というものがあるものだろうかとよく空想するものですが何の事はない
負の質量を持つ重力場の中で生まれてその中で生活しているのですね。