Mystery of Log Log Scales
Acknowledgement: The following knowledge was given to me through discussions at "Slide rule mailing list". I am especially thankful to Messrs. Dave Martindale, Ted Stern, Duane Croft, Fritz, Ron Manley and others for their input.
Log Log (LL) scales are used to calculate powers of a number such as 2.341.56. Basic theory is that by taking two times logarithm of expression Xa, one gets log(a) + log(log(X)), thereby converting powers of a number into an addition.
For example, Figure 1 below shows calculation of compound interest rate at annual rate of 1.5%. First, left end of C scale is aligned with 1.015 on LL1 scale (1). Compound rate for any number of years can be obtained by setting the cursor on a desired number of years and reading appropriate LL scale. For 2 years the compound rate is 3.02% as shown by the rightmost arrow (2). To get the rate for 12 years, the cursor is set at 1.2 on C scale and rate is read off on LL2 bacause we are dealing with a number which is one order of magnitude larger . The answer is 19.6% on LL2.(3)

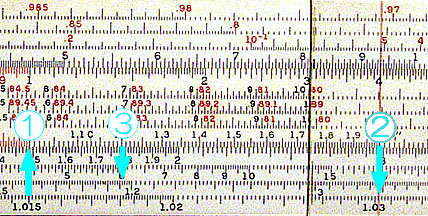
Figure 1. Finding compound interst rate at annual rate of 1.5% (Ricoh 151)
We observe that an LL scale begins with even number such as 1.1, 1.01 or 1.001, except for LL2, which appears to begin at natural number "e". Further more, 1.1 and 1.01 are not on exact origin of the other regular scale such as C or D.
If you take two times logarithm of 1.1, you get log10(log10(1.1)) = -1.383076 = -2 + 0.616924. Since mantissa is about 0.6 we would expect the mark at a little bit right side of the center. But it is not there.
It is because "base" of logarithm can be selected arbitrarily, as long as relative alignment between LL scales is kept. But then, what is the base?
As I found out, natural number e is chosen for the most slide rules. Advantage of doing so is that one can obtain natural logarithm values on D scale.
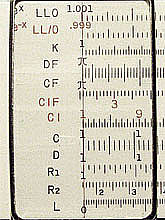
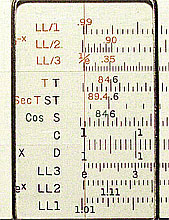
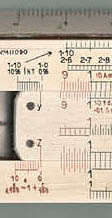
Figure 2. LL Scales at Left end (Post 1460)
Taking e as the base gives us another convenient coincidence. That is, all the numbers 1.1, 1.01, 1.001 come close to the origin, making it easy for us to handle the numbers.
Dave Martindale taught me why it is so.
He says it can be explained using aproximation expression; ex 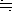 1 + x, where x is close to zero.
1 + x, where x is close to zero.
Well, not so fast, Professor.
So, if we take natural logarithm of both sides, we get;
x 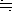 ln(1+x)
ln(1+x)
At this point, we assume x = 0.001 and take base 10 logarithm;
-3.0 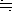 log10(ln(1.001))
log10(ln(1.001))
There, since fractional part of the left hand side represents location on the slide scale, it is close to the origin of either C or D scale.
Therefore, 1+x comes close to the origin whenever x = 10-n where n is a positive integer.
Log log scales of the most of 10 inch rules come as set of 8, including LL0, LL1, LL2, LL3 and their inverse scales.
However, most of the 5 inch rules do not have the LL0 scale. What would you do if you wanted to find out what is the compound interest rate of 0.3% per year (corresponding to; x = 1.003) over 13 years?
Answer is to use D scale for LL0 scale. You interpret the left end of D scale as 1.001 and right end as 1.01. Thank you Duane Croft and Dave Martindale for the information.
Figure 3 below illustrates the above example. Set left end of C scale at 3 on D scale and set the cursor at 1.2 on C scale. The answer 1.0366 is found on LL1 scale since 12 is one order of magnitude up.
This method is remarkably accurate. Error is about 0.2% (in terms of length) at the right end of the scale and is almost zero at left end of the scale.
I was informed that this technique is described in K&E slide rule mannual.

Figure 3. Using D scale in rue of LL0 scale (Pickett N600-ES)
While the above method seems sufficient for most cases, Ted Stern, Fritz and others informed me a method of obtaining further accuracy.
The method is obtained by considering Taylor expansion of the function ln(a+x).
ln(a+x) = ln(a) + x/a - x2/2a2 + x3/3a3 - ...
Setting a = 1 and taking remaining two most significant terms, one gets;
ln(1+x) 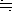 x - x2/2 = x(1-x/2).
x - x2/2 = x(1-x/2).
Now we take logarithm of base 10 of this equation.
log10(ln(1+x))  log10(x(1-x/2)).
log10(x(1-x/2)).
We see that left hand side represents the location of 1+x on loglog scale, and right hand side represents location of x(1-x/2) on D scale.
This means that, instead of using x, we calculate x(1-x/2) and set this value on D scale. This is very similar to the previous method. Only difference is that we utilize (1-x/2) as "correction factor" to x.
For example, for x = 0.01 (asuming we want to set it on the right end), we calcurate 0.01*(1-0.005) and get 0.00995. Therefore, we see that 9.95, instead of 10.0 is more accurate point for 1.01. The error by this method is remarkably small at 0.001%!
The actual point which 9.95 is located is at 99.8% of the scale length, or 0.25mm left of 10.0 point on a 5 inch rule. Actually, one can read this length on the left side of the scale. Difference between 1.01 on LL1 scale and 1.0 on D scale is the "correction factor", so to speak.
Since the correction required is so small, perhaps one can apply the necessary correction by noting the maximum amount and mentally creating adjustment length and applying "a little nudge" to the slide. Sounds analogic? Why not? It's an analog world after all.
 If you have an "Elecrical rule", your rule may have LL2 and LL3 for Log Log scales. In this case the lowest rate you can go is 10%. However, if you have a Thornton with "Log Log Differntial scale", you are in luck.
If you have an "Elecrical rule", your rule may have LL2 and LL3 for Log Log scales. In this case the lowest rate you can go is 10%. However, if you have a Thornton with "Log Log Differntial scale", you are in luck.
The patented Log Log Differential scale let's you compute the interest rates as low as 1% without LL1 scale.
This "Differential scale" can be considered as an axurially "Correction factor" similar to the situation in Mystery 3 in which we discussed how to use D scale for LL0 scale.
Example: What is the compound interst rate for an annual rate of 2% for 16 years?
o Set y index on slider to 2% on Int scale and move the cursor to 2.0 on C scale. Now you have corrected value of LL1 for 1.02 (2%) on the D scale.
o Move index (either 1.0 or 10.0, 1.0 for this example) of the C scale to the cursor line and move the cursor to 1.6 on C scale.
o The answer 1.373 (37%) is found on LL2 scale.
 William Oughtred invented modern slide rules in 17th Century. Oughtred Society is an organization for slide rule lovers and collectors.
William Oughtred invented modern slide rules in 17th Century. Oughtred Society is an organization for slide rule lovers and collectors.
Quoting from the Society's webpage;
"Members are provided with an annual subscription to The Journal of the
Oughtred Society, along with a membership directory. Membership privileges include the ability to purchase back issues of The Journal,
to attend and participate in annual meetings, and to receive our annual swapsheet."
If you are a slide rule enthusiast I highly recommend to join the Oughtred society.
There appears to be several different nomenclatures for the Log Log scales. Some manufacturers also implemented Log Log scales in their special way.
| Mfr | Nomenclatures & Features | Ref. |
|---|---|---|
| Faber Castell | LL0, LL1, .. , Inverse scales are named as LL00, LL01, .. LL0 scale for 2/83N Nobo Biplex is shared with D scale. Right hand side of D scale bears modification figures. For example, at D = 10.0, small numbers are added in front and at back, thus, 1.0 10 05. It is telling us that at D = 10.0, LL0 is equal to 1.0105. The real LL0 = 1.01 is at a little to the left. |
2/83N 63/83 |
| Hemmi | LL0, LL1, .., Inverse scales are named as LL/0, LL/1 ... In certain rules, inverse scales are named as LL00 - LL03.. | 259D P261 |
| K&E | K&E rules have at least three different ways for naming Log Log scales which appears to have gone through generational evolution. The 68-1100 Deci-Lon, the newest generation, bears Ln0 - Ln3, and reverse Ln-0 - Ln-3. In the case of N4081-3, which is one genaration older, bears names such as LL1 - LL3, and reverse scales LL01 - LL03. The third system is used for older rules such as 4080-3. In this rule forward scales are; LL1 - LL3, and reverse scales LL0, LL00. In this case LL0 corresponds to LL1 and LL00 corresponds to LL2. | 68-1100 N4081-3 4080-3 |
Pickett | Pickett had their special way of implementing Log Log scales which is called "Dual Base". In this arrangement, forward and inverse scales are paird and drawn on upper and lower side of a line. In addition to the advantage that one can find inverse of a value rapidly, it uses less space and enable to draw more scales on a slide rule. Other Pickett rules has LL1 - LL3, and reverse scales LL0, LL00. This scale set is the same as K&E's earliest scale set. | N803ES 500T |
| Post | Post has the same scale set as Hemmi. Forward LL0 - LL3, and reverse LL/0 - LL/3. There are rules which has LL1 - LL3, and reverse LL0, LL00, which is the same set as K&E. | 1460 1462H |
| Ricoh | Ricoh's rules have LL1 - LL3, and reverse LL1- - LL3-. The upper bars are actually above the last numerals. | 151 |