数学小話らんど <<BACK>>
ここでは、数学の(超くだらない)小話を集めてみました。皆さんから面白そうな(くだらなそうな)話をお寄せいただければ幸いです。
第1話(しもまっち)
八: y=mx+n と、y=m’x+n’ が垂直のとき、mm’の値はいくつになる?
熊: 垂直か。 ⊥ だね。![]() わかった! mm’=−1
わかった! mm’=−1
八: ・・・・・・
第二話(しもまっち)
八: 2-1はいくつ?
熊:2-1か・・・。
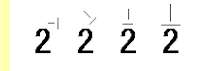
わかった、1/2 だ!
八:しぇ〜
第3話(しもまっち)
隠居:虚数のことを、imagenary number といい、その頭の i をとって、虚数単位を i と表すんだよ。
熊吉:なるほど。ってことは、 i がついている数が虚数ってんですね。じゃあ、 i がついていない数は虚数じゃあない、
つまり、虚(うそ)の数じゃあないんですね。
隠居:そう。imagenary number から、i をとると、 magenary number となるだろう。
つまり、マジナリ(マジ也→まじな数→実数)というわけだ。
熊吉:ぎゃふん。
第4話(しもまっち)
妻:私はあなたと結婚してからというもの、あなたの世話ばっかり。あなたは好きなことばっかりで得ることがいっぱいだけれど、
私は減ることばっかりだわ。
夫:男はプラス(+)を重ねて父になり、女はマイナス(−)を重ねて母になるというじゃあないか。


プラスを重ねると掛け算になる マイナスを重ねて割り算になる
妻:とほほ。
第5話(トラディショナル)
熊:あのなー、次のなー、計算をよー、できるかよ。
八:どんな計算だい?
熊:じゃあいうぞ。あのなー、1たす、2たすなー、3たすなー、4たすなー、5だよ。
八:ああ、1+2+3+4+5かい。それは15だな。
熊:違うよ、「1たす」「2たすな」「3たすな」「4たすな」「5」だから1+5で6だよん。
八:とほほのほ。
第6話(しもまっち)
達:バレンタインデーでチョコをもらったお返しに何やればいいんだべ。
純:そりゃあ、チョコパイかアップルパイだね。
達:なんで。普通はキャンディとかだろ。
純:だって、ホワイトデーは3月14日だろ。3.14だからパイ(π)なのさ。
達:さいでっかー。ここをクリック
第7話 数学者駄洒落らんど
10歳のガウスが、ウッスと元気に挨拶して1〜100までの計算を一気に済ませた。
「パリ科学アカデミー審査員のコーシー様。お飲み物は何にいたします?」
「コーシー」
「πとか、eとかの記号を考えた人って誰だろう?」
オイラー「そりゃ、おいらだ」
「あそこの水槽の中の魚と、そばに立っている高校教師は?」
「ああ。出目金と、デデキント」 ( 註 デデキントは晩年高校教師を務めた)
デカルト「私は野営で夢を見た。それで座標系の考えを得た。でもそのとき、草がぼうぼうで大変だった。」
「草は、鎌で刈るといいですよ」
「パスカル様、多項式の展開が難しいです」
「じゃあ、わしの作ったこの三角形をつかってみい」
「ああ。ありがたい。これでパスカル(助かる)」
アルキメデスとピタゴラスが、アテネのスタジアムでマラソンに参加した。
「ピタゴラスさん。最初は先頭集団にぴったりついていましたが、後半は最下位になってしまいましたね」
ピタゴラス「これが本当の、ピタ、後、ラスさ」
「アルキメデスさん。途中走っている姿が見えなかったんですけれど・・」
「途中から、歩き、です」
「非ユークリッド幾何学のロバチェフスキーさんの趣味もやっぱり数学ですかね」
「いや、チェスやゲームが好きだったそうだよ」
「ロバ、チェス、好き、か」
「ペアノさんの趣味は何ですか」
「ペアノ(ピアノ)」
「クラインさんちょっと電気つけてください」
「どうしてですか」
「暗いんです」
「マルコフさんの娘さんの名前は?」
「そりゃ、ちびマルコフさんじゃよ」
4人の数学者がマージャンをやっている
「よし。危険牌捨てるぞ、それ、フーリエ!よし、通ればリー」
「ポンスレーばいいかな」
「なくなよ。リーマン(リーチマージャン)やろうぜ」
「ブールバッキというのは1人の数学者じゃなく、フランスの数学者集団の名前なんだよ。この集団が、
現代の数学の構築に大いに寄与したんだ。ところで、最近ワイルズによって証明されたフェルマーの
定理には日本人の谷山、志村はじめ多くの人間が関わっているよね」
「そっかー、てことは、ワイルズって、あのリーマン幾何学の研究で有名なワイルとその他の人々ということ
だったのかー」
とりあえずここまで
第8話(学生時代に書いた(1976)、はちゃめちゃSF?小説)〜これは小話ではないのですが・・・数学、でもないのですが・・・・
<1>
いつになくギニーはみょうにしなをつくりながらセントポールに言うのだった。
「ねえポール。今夜のいかだの群れはタイワンアカイエカを思い出すわ。」
ポールは左足の爪を切る手を休めもしないで、かぶりを振った。
「君のいていることはムカデダマシかヒトデモドキというほかないね。第一今夜の月は御影石じゃあないか。はりこのうちわもそこらじゅう飛び回っているぜ。」
ギニ−は黙ってしまった。それはポールの言葉に反抗できなかったからではなく、足元のオンブバッタのとんがった頭にふと今日通ったパリの街並みを思い出したからであった。そして、目に涙を浮かべると、キリマンジャロの高原で一人こけをむしるかのようにこういった。
「ポール。もう一度パリのエッフェル塔にのぼって、2人でマスターマインドをしましょう。」
ギニーの目はトビイロゴキブリのように真剣だった。
「イモムシのようにもう一度行くというのか、ギニー。ここはナスカ平原じゃないんだぜ。たのむからダスティローデスとチェーンマッチをするようなことだけは言わないでくれ。」
とポールは言って、爪を切るのをやめ、タバコをくわえた。
「でもあなたがくわえているの私のタンポポよ。」
「ああ、もちろんさ。ただしリーマン面上の話だがね。」
ポールは冷静であった。最後の言葉では、ギニーに指を突きつけながらさえ言うのであった。ギニーは心の中でつぶやいた。
「何としてもポールに首吊り人形を食べさせねば・・・。でも一言ウェザーリポートといったら全てが終わってしまう。
<2>
2人の歩いている道はクルマバッタの死骸が散在しているわりにはみょうに浮き足立っていた。階段には、殆どいたるところで、絡め餅にひっかかったイカシオカラとカイガラバッタがカラテオドリを踊っていた。
「ふん。この長崎かすていらはちっともムカデよい味じゃあないじゃないか。そればかりか少しけやきくさい感がある。」
「ええ。でもとってもけまこい味よ。すらべちいかぎりだわ。」
2人の会話はポールの食べていた仙台味噌饅頭に終始した。しばしの沈黙の後、今が最後のチャンスと思ったのだろう。ギニーはポケットの中のピストルに玉が入っているのを確かめた後、素早い右手の動作で玉葱を剥きだした。
「なるほど。勝利の女神はいつまでも主イデアル整域と共に生きるというのは、単なる神話ではなかったか。」
ポールは落ち着こうとしたが流れ出る汗は止めようがなかった。
「ふん。かいばぐいがはげしくなったわね。ポール。あなたもただのプレシオザウルスよ。」
正直言ってギニーはこの言葉をどうして思いついたのか自分でもよくわからなかった。あのデザルグの定理を、パスカルの定理だけを使って証明したときでさえ、こんな素晴らしい考えは思いつかなかったのだから、まさに勝利の女神はジムグリガエルそのものだったといえよう。
<3>
「いいことポール。あなたの仕事はヤスデのパンティストッキングを編むことよ。わかった。」
ギニーは右手の親指をちっとも曲げないで、それどころか、左足の関数の値を恒等的に0にしながらこう命令したのだった。しかし、ポールは一瞬思いつめた態度をとった後、すぐ覚悟を決めて、快心の微笑とともにこう言い出した。
「ろろろろろろろ・・・・・・・・・」
こういう勝負手があったのである。”際限無く『ろ』を続ける”ことによって、ギニーはポールの真意を図りかね、『ろ』の連鎖が終わるのを待つばかりであった。が、それが10分と続くと、ポールの真意をやっと理解し、そして、それはギニーに対する大変な勝負手であることがわかった。
ポールは際限無く『ろ』を続けるであろう。そして、『ろ』の連鎖を自分で打ち切ったときポールは敗北者となる。ところが、ギニーが、ポールの意図は”加算無限個の『ろ』を繰り返す”ということを知ってしまった(実際そのことを知るのに彼女は10分を費やしたが)以上、ポールが十分大きなnに対して、『ろ』をn個続けて打ち切ってしまってもポールは勝利者になることが確実なのである。
すなわち、ギニーがポールに対して勝利者になるには、−もちろん賢明な読者はもうお気づきと思うが−ポールの『ろ』の列が始まるや否や、
「あなたの真意はわあっているわ。でもそんなことではハイネボレルの被覆定理は証明できませんことよ。」
というほか無かったのである。しかしもう取り返しはつかない。ギニーはポールの『ろ』の音の渦の中で何とか自分を取り戻そうとした。ギニーは心の中で「やはり勝つことはできない。恐ろしい手だわ。ブリアンションの美濃矢倉以来のできだわ・・・・・。でも引き分けることはできる。穴熊には居飛車穴熊」とつぶやいくや、ポールに負けない大きな声でわめき始めた。「れれれれれれ・・・・」ポールの『ろ』とギニーの『れ』は競争心を剥き出しにしてエスカレートしていった。2人は目を剥き出しにして、額に玉の汗をかきながら頑張り続けた。
『ろろろろろろ・・・・』『れれれれれ・・・・・』 なぜなら、これを先に終えたほうが確実に敗北者になるのだから。 <完>
書いたときは筋が通っていたと思っていたんですが、おもいっきりはちゃめちゃですね。
第9話(学生時代に書いた(1976)、はちゃめちゃSF?小説2)
超売れっ子トレンディ博士の天馬教授は、現代の若者のアイドルであった。
彼の言動は、その当時の若者のファッションやライフスタイルに大きな影響を与えていた。
その天馬教授が某大学で、講演を行った。演題は「人間の新しいコミュニケ−ションについて」。
多くの学生を前にして、博士の話も普段より熱がこもっていた。
「・・・・・言語というものを、時系列、つまりマルコフ過程的に解釈した場合、一定時間内にあまりにも多数の情報を送り込むことによって、
むしろあいまいさがだけが際立つのです。音楽を見なさい。
あなたたちはジャズピアノの速いパッセージの音や音たちの順番がきちんと理解できますか。いや、わからないはずです。」
というと、博士は、演壇のわきに置いてあった古いアップライトピアノの前に腰掛け、いきなり、ぎゃろんぎゃろんぎゃぺぺぺきゃりこれら、
と、髪を振乱し、凄い勢いでめちゃめちゃに弾いた。
学生達は一瞬はっとしたが、うなずいたり、中には感動で目を見開いている者もいた。博士はやおら演壇に戻ると、呼吸を整え話を続けた。
「ところが、ところがですよ。このような多数のめちゃめちゃな音列にもかかわらず、人々はその音楽全体にある種の感動を覚えるのです。
つまり、むだなもの、冗長性があるために、一層、中の情報量が浮かび上がってくるのですね。・・・・・・・・
人間の頭脳のシナプスの状態を、n次元ベクトルで表してみましょう。(a1,a2,a3,・・・・an)、ここで、aj=0 or 1 とします。
このaj が0か1かの値をとって、一つの状態を形作ります。例えば(1,0,0,1,1,0,・・・,1)ですね。
このように考えると、さっきの音楽の例に戻った場合、一定時間内に多数の情報を織り込み、
そして、そのエントロピーが増大するような方向を示すと、頭脳のn次元ベクトルの状態のテンションが高まり、
その符号語が増加するわけです。このことは、簡単に言うと、頭の働きが早く、活発になることを意味します。
逆にいうと頭の働きが早い人ほど多くの状態ベクトルを持っているといえましょう。」
学生達は、本当はわけがわからなかったが、必死に数式をノートにうつしたり、さかんにうなずいたりしていた。
「・・・・・ですから、これからの人間のコミュニケーションは、」博士はようやく結論に入ろうとしていた。
「例えば、『腹が減った』ということを相手に伝えるとき、それを相手が理解したシナプスの状態が、(b1,b2,b2, ・・・・・,bn) だとしたら、
そのようにシナプスを刺激する話し方がいく通りもあるはずです。
ですから、『まどふきおじさんがいつになく犬のしっぽを踏みにじったね』でいいかもしれませんし、
また、そのときの天候や雰囲気によっては、『じゃがいものたねは白いきりぎりすだ』でよいかもしれません。
つまりこれからのコミュニケーションは、頭脳のシナプスの状態の新しいパターンを見つけていくことなのです。
また、こういったコミュニケーションをとれる人々こそ、頭の良い人なのです。」
博士の講演が終わった。聴講していた学生達は口々に感想をいいあった。
「きょうの博士はエントツの吹き溜まりがコンニャクを食ったみたいだったわね。」
「いや、それより私はあの大森山の電気コタツを思い出したわ。」
「そうかな。南部馬追い虫にも似たこけむしりじゃあないかな。」
「というか、オキアミ漁船のテレビ放送が長島監督の耳元で・・・・・」
学生全員がいいだした。そしてそれは延々と続いた。
完
学生時代に書き散らかした恥ずかし小説第2弾でした。当時情報理論をやっていたことと、筒井康隆や山下洋輔の書いたものなどに影響を受けてこんなものをかいたのでせう。
数学小話探訪の旅はまだ続く・・・