パズルの解を増やす手法 <<Back>>
1 合同変換
パズルの中に、以下のような合同図形を織り込めば、その図形を交換することによって、新しい解を得ることができます。

例えば上図の場合は、3つの合同図形があるので3!=6通りの変化があります。
2 対称変換
パズルの中に、以下のような対称図形を織り込めば、その図形を対称移動することによって、新しい解を得ることができます。
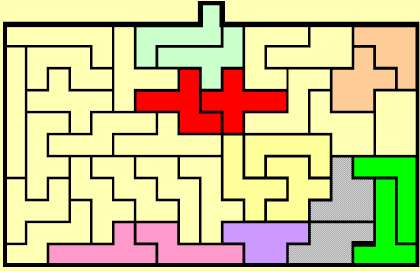
上図は2つのピースでできる対称図形を中心に織り込んだものです。対称変換できる図形を沢山入れることによって、
パズルの解の個数はは飛躍的に増えていきます。
3 回転変換
これは、対称変換の1つの応用です。図のように回転可能な図形を織り込むと、パターンが増えます。下図の例のほか、
正方形も回転変換可能な図形です。

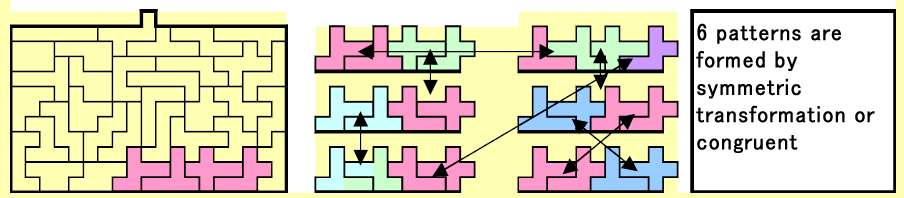
4 合同変換と対称変換の合成
これも対称変換と合同変換の応用例です。私はこのパターンに「スライド」と名づけました。対称変換と合同変換が波及しあう面白い変化です。生じる6種類の図形はもちろん2つの変換に対して閉じているわけです。
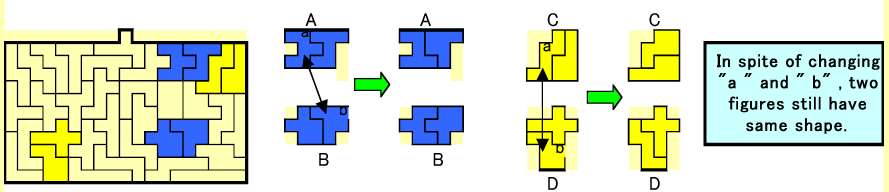
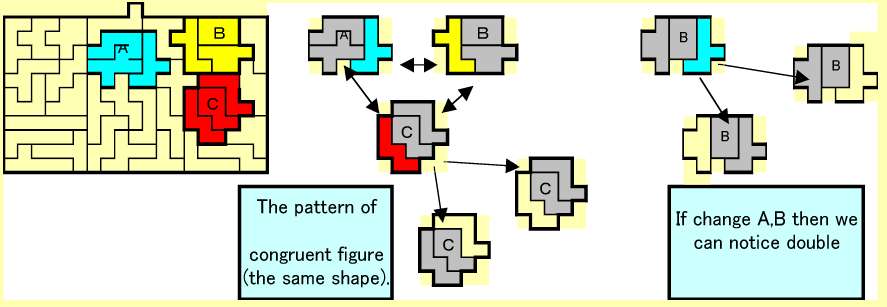
5 奇妙な合同変換
ちょっと変わった合同変換を紹介します。A,B,Cの3つの図形は互いに合同です。特にCに注目すると、合同図形が2つ重なっていることがわかります(中段の図)。今、例えばAとBを交換したとしましょう。すると、今度は右図のように、A部分に合同図形が2つ重なります。
6 共役類変換
図のA,Bは合同図形ではありませんが、Aのaと、Bのbを入れ替えても、ともに同じ図形が再現されます。C,Dについても同様です。