パターンの多い解

　　　　　 パターンの多い解

　ここで紹介する解は、対称変換、合同変換を行うことによって多くの変化を持つものです。

これは私が２０年前くらいに作ったもので、「Infinity」と名づけました。

パターンのいくつかを紹介して、これから得られる解の総数を予想してみましょう。

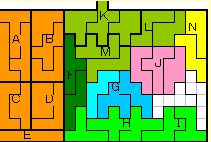
　Infinity　　　　　　　　　　　　　　　　　左側　　　　　　　　

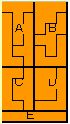
Ⅰ　左側ABCDE部分の変化（上図茶色部分）

　まず、左側部分の変化を調べてみよう。上図のような状態のとき、

４^３(ABＤ)×２(C)×3!（ABとCDとＥの並べ替え）×2(ＡとＢの入れ替え)×2(ＣとＤの入れ替え)

＝３０７２

　また、この部分は対称合同変換を繰り返すことで以下のようなバリエーションがある。

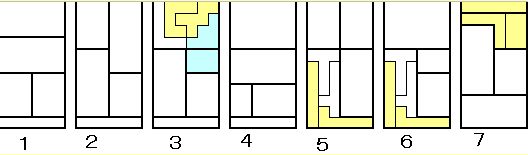
　１　４^３(ABC)×２(D)×４!（A、B、CD、Ｅの並べ替え）×2(ＣとＤの入れ替え)＝６１４４

　　２　４^３(ABC)×２(D)×2(ＣとＤの入れ替え)×２(AとBの入れ替え)×２(Eとの入れ替え)＝1024

　　　　２から色つき部分を合同変換して３のパターンが得られる。

　　３　４^２×２×２×３!×２＝７６８　　　更に、３から変化して、

　　４　４^２×２×２×４!＝１５３６　　　　４から色つき部分を対称変換して

　　５　４^２×２×２×２×２＋４^２×２×２×２＝３８４　　　更に変化して

　　６　４×２×２×２×２＝６４　ちょっと特殊な変換を加えて、

　　７　４^２×２×２×２×３!＝７６８

　　さらに５の変化の途中で、右側部分のＮと合同図形が生じて、それを入れ替えたときの変化が

　　１２８×２５２＝３２２５６　（図は省略）　・・・・（※）

　　以上より、とりあえず左側部分の総数は、

　　3072+6144+1024+768+1536+384+64+768=13760 　　(※は加えない）

Ⅰ　右側部分の変化（上図中央）

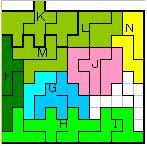　　図において、Ｐ及びＪは対称図形なので、２×２＝４

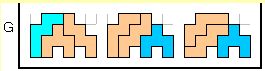
また、Ｇ部分は対称図形が２重に重なっているので　３通りの変化がある。

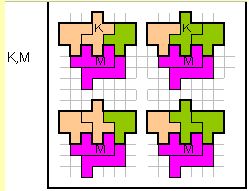
　次にＫ、Ｍの部分だが、図のように、Ｋ部分が４通りに変化して、そのおのおの

に対して、Ｍと合同変換ができるので、４×２＝８通り。

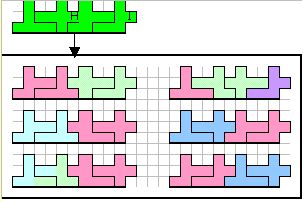
　Ｈ，Ｉは対称変換と合同変換で６通りの変化を見せる（スライドと名づけた）。

　ここまでで、右側パターンの総数は、４×３×８×６＝５７６

　ところで、Ｋの変換の際に、Ｉと合同な図形が生じ（図略）、それを入れ替えたときの

　バリエーションは、４×３×４×２×２＝２８８

　よって右側部分の変化は、５７６＋２８８＝８６４

以上より、解の総数は、（※）も含めて、

　１３７６０×８６４＋３２２５６＝１１,９２０,８９６　通り

　（右側と左側の入れ替えは解に入れていない）

　計算の間違いはあるかもしれませんが、少なく見積もっても、この１つの解から１０００万以上

の解が生まれると予想できます。　更に、この解の左側部分を残して、右側部分を作り

直しても沢山の解が得られます（私はとりあえず変化解として約200万通り作りました）。

そんなことから、左側がこの「Ｉｎｆｉｎｉｔｙ」のような場合だけで何億という解ができることが