|
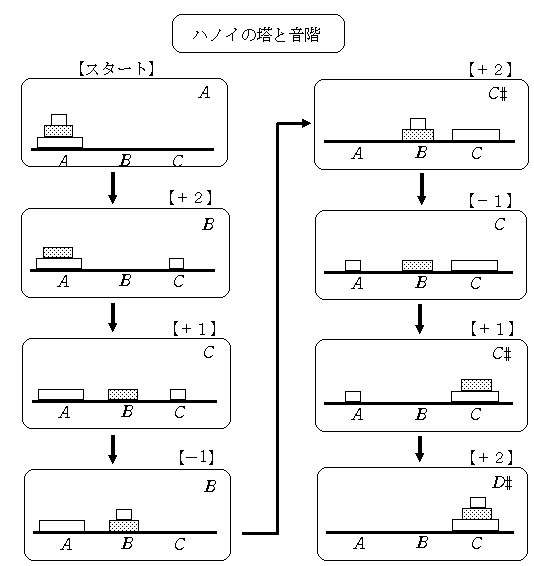
【説明】 右図の3枚のハノイの塔で説明する。 各板の移動は、 A→B (+1) A→C (+2) B→C (+1) B→A (-1) C→B (-1) C→A (-2) の6通りであり、それぞれの移動距離、1、-1,2、-2を割り振る。 このとき、移動距離を音階の移動と考える。つまり移動距離±1の時は、半音、±2のときは全音の上昇または下降と考える。 図の場合は、スタートをA(ラ)として、そこからハノイの塔の手順に従い、上昇と下降を繰り返すことで、全部で8音からなるスケールができあがる。
|
|
ハノイの塔の音階①
|ハノイの塔の音階②|ハノイの塔の音階③|HOME|音楽&数学らんど|
|
【説明】 右図の3枚のハノイの塔で説明する。 各板の移動は、 A→B (+1) A→C (+2) B→C (+1) B→A (-1) C→B (-1) C→A (-2) の6通りであり、それぞれの移動距離、1、-1,2、-2を割り振る。 このとき、移動距離を音階の移動と考える。つまり移動距離±1の時は、半音、±2のときは全音の上昇または下降と考える。 図の場合は、スタートをA(ラ)として、そこからハノイの塔の手順に従い、上昇と下降を繰り返すことで、全部で8音からなるスケールができあがる。
|

|
【ハノイの塔(3枚)の音階】 上の手順で出来上がったスケール
|
|
この手順に従って、枚数を多くして音階を作っていきます。
この手法だと、全音より大きい音の変化は無く、うねうねとした音階が続きます。
またハノイの塔の手順が、自己相似的なので、音階も自己相似的になり面白い。
追記: ところで、この音階はハノイの塔を最短で移動させる場合のパターンですが、
ハノイの塔のルール(1度に1枚の移動・小さい板の上に大きい板を置けない)に従って、
任意に板を動かすことで、いわばハノイの塔上でのランダムウォークの音階を考えることもできます。
これは、単なる1,-1,2,-2の任意の並べ替えにより作られる音階ではなく、ハノイの塔のルールから、
2と2、-2と-2が連続しないこととか、1,-1はそれぞれ最大3個までしか連続できないとか、いくつかの制約
のもとで作られるので、単なるブラウンノイズ(褐色雑音)とは異なります。
また、板の大きさに応じて重みをつければ更に変化した音階ができるでしょう。