

│Grapesの世界へ│面白数学らんど│音楽&数学らんど│リンク│エクセルで面白数学│ホーム│
あなたもGrapesの世界へ④
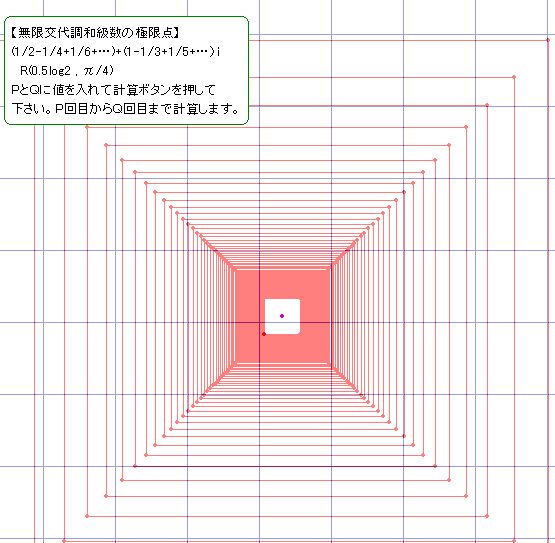
無限調和交代級数
1-1/3+1/5-1/7+・・・ という無限級数は、π/4に収束することが知られているし、また、
1/2-1/4+1/6-1/8+・・・という無限級数は、(1/2)log2 に収束することが知られています。
どちらも、左辺=「有理数の加減」なのに、右辺は超越数になるのが、なんとも不思議で
すね。これが無限の面白いところでしょう。
さて、この証明は高校の微積分でわりと簡単に求めることができますが、
ここでは、この2つの級数の収束の様子を、Grapesを使って眺めてみましょう。
 |
Grapesのスクリプト機能を使って、簡単なプログラミングをします(左下図)。pとqに値を入れて「計算」マクロを実行すると、左図のような渦巻きを描いてくれます。この渦は、極限点、P((1/2)log2, π/4)に向かって進んでいることがわかります。 最後の方は見えにくいので、「指定領域の拡大」機能を使って、中心部分を拡大します。そして、更に、p、qの値を大きくして、移動回数を多くしていきます。何度もしつこく拡大してみましょう。自己相似的に、どんどんPに向かっていく様子がわかります(下図)。 | |
  |
||
上のような点(複素数)の移動によって、極限点が得られる理由を、複素関数を使ってごく簡単に説明します。
