│Grapesの世界へ│面白数学らんど│音楽&数学らんど│リンク│エクセルで面白数学│ホーム│
あなたもGrapesの世界へ②
アステロイドと三倍角の公式 GIFアニメを見る
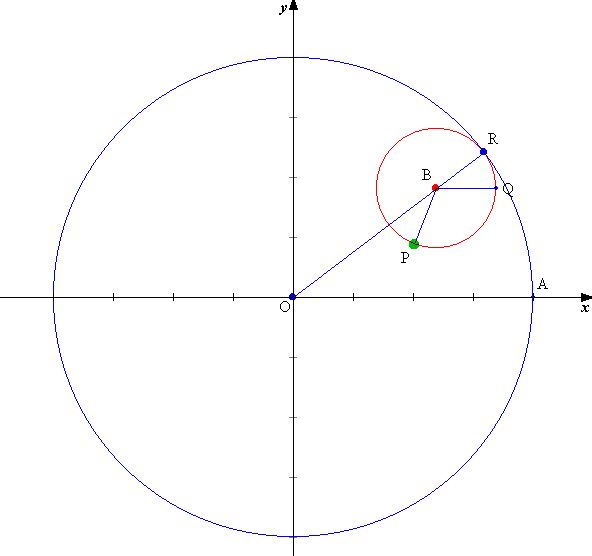
下図のような半径4の円に、半径1の円が滑らずに内接しながら転がるとき、小円の固定点P
の軌跡はどうなるか、という問題を授業で扱ったときの話です。これはアステロイドという曲線になるのですが、
実際にグラフィクスで動くところを見せないと意味がありません。そこでGrapesを利用して、描画する方法を考えました。
まず、∠AOR=θとして、Pの座標を、θで表せばいいですね。今、弧ARと弧PRが等しく、AR=θなので、
PR=4θとなります。すると、∠PBQ=3θです。すると、B(3cosθ,3sinθ), ベクトルBP=(cos3θ,-sin3θ)なので、
OP=OB+BP というベクトル和で考えて、P(3cosθ+cos3θ,3sinθ-sin3θ)と表せます。
ところで、アステロイドは、x^(2/3)+y^(2/3)=4 つまり、x=4cos3θ, y=4sin3θとパラメータ表示されることが知られています。
ということは・・・なあんだそうか。4cos3θ=3cosθ+cos3θ つまり、cos3θ=4cos3θ-3cosθ
4sin3θ=3sinθ-sin3θつまり、sin3θ=3sinθ-4sin3θ
アステロイドのパラメータ表示は、三角関数の3倍角の公式の図形的な意味なんだ。
