│Grapesの世界へ│面白数学らんど│音楽＆数学らんど│リンク│エクセルで面白数学│ホーム│

あなたもＧｒａｐｅｓの世界へ�K

Ｇｒａｐｅｓで対数法則

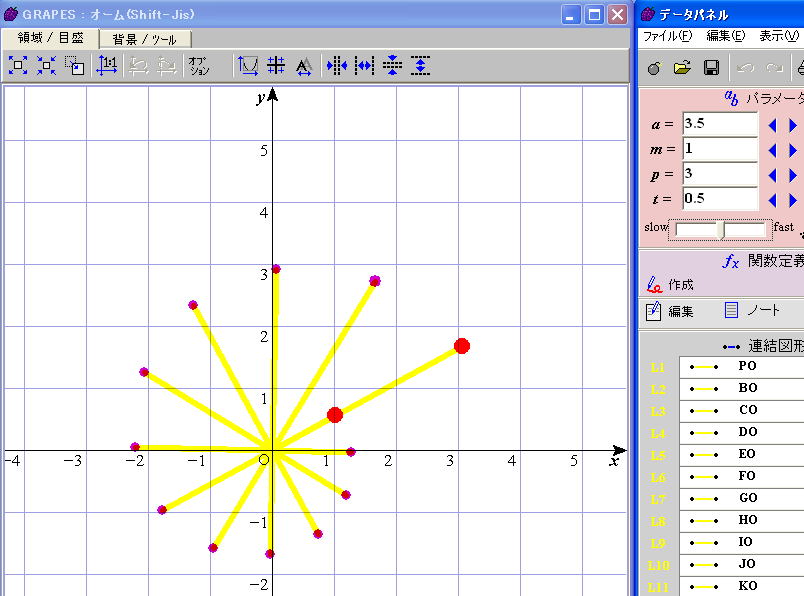
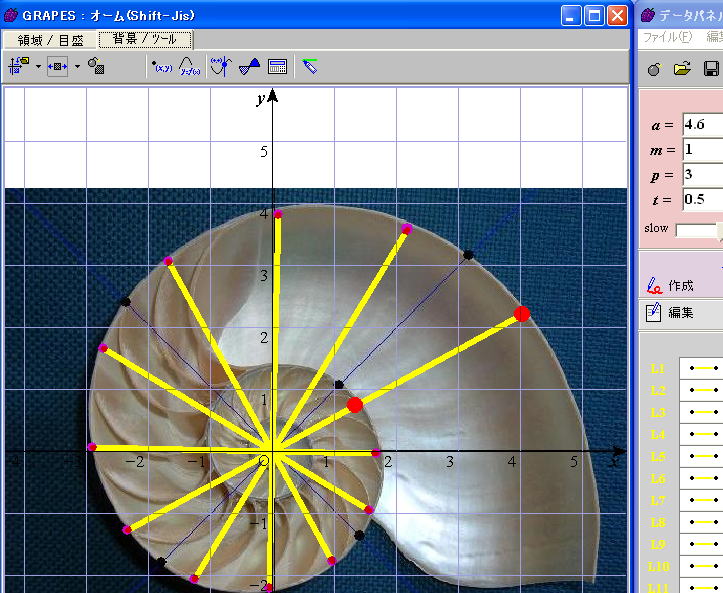
グラフ描画ソフトGRAPESを使って、上図のように、時計回りに30°回転するごとに倍になるような12個の動径を作ります。つまり１回転すると3倍になるように動径が変化しています。また、初期値の動径は自由に長さを変えたり、好きなだけ回転できるようにします。GRAPESでは、グラフの背景に図を挿入することができます。そこで、これにオウム貝の断面の写真を貼り付けてみました。何と！驚くことに、12本の動径がぴったりと重なりました（図１）。つまりオウム貝の中心からの半径は指数関数に従って変化していることがわかります。オウム貝の成長曲線が指数関数的であることは、偶然や神秘という言葉で片付けられるものではなく、「瞬間の成長率はそれまでの蓄積量に比例する」という原理を、という微分方程式にすることで導かれると考えられます。ピタゴラスは「万物は数である」といいましたが、まさに、数学は自然現象を語る言語であることが改めて認識できます。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
12本の動径を1回転して2倍になるようにしてみました。もちろんオウム貝とは重なりませんね（左下図）

ところが、動径の間隔の角度を30°から19°に変えてみるとあら不思議、12個の動径はオウム貝にぴったりと重なりました（右下図）なぜでしょう。

そう。これは底の変換です。　で、は約0.63なので、

30°×0.63＝18.9から約19°間隔にすればよいのです。

（）

このように、間隔を変えれば、どんな底の指数関数もオウム貝の中に実現できることがわかります。