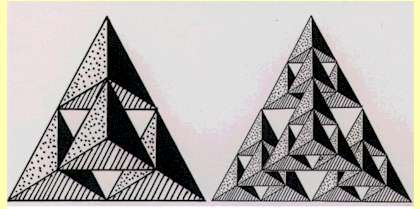
シェルピンスキの立体ギャスケット　　　<<Back>>

　シェルピンスキのギャスケットにヒントを得て、その立体版を考えてみました（1989）。

作り方は、正四面体の四隅から４つの相似正四面体を残し、

内側の部分を抜き取るという操作を繰り返していくという方法です。

これは立体なので作図しにくいのですが、全体を１／２倍に縮小したものを４つ集めて自己再現される

ということに気付けば、コピー機を利用して、縮小コピーを駆使すれば簡単に図示できます。

最初の正四面体の体積を１とすれば、第ｎ代目の体積は（１／２）^{ｎ　となり、}

^{ｎ→∞で、体積 ０ となります。}

^{また、この図形の相似性次元をDとすると、D=ｌｏｇ}₂^{４＝２次元　となります。}

^{尚、４つの正四面体でくりぬかれた図形は8面体になりますが、そちらを図示してみても面白いかもしれません。}